青岛版数学八年级下册6.3 特殊的平行四边形(2矩形的判定) 课件(15张ppt)
文档属性
| 名称 | 青岛版数学八年级下册6.3 特殊的平行四边形(2矩形的判定) 课件(15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 08:22:56 | ||
图片预览



文档简介
课件15张PPT。6.3 特殊的平行四边形(2)青岛版数学八年级下册1.了解矩形的判定方法。
2. 能综合利用矩形的性质与判定解决问题。
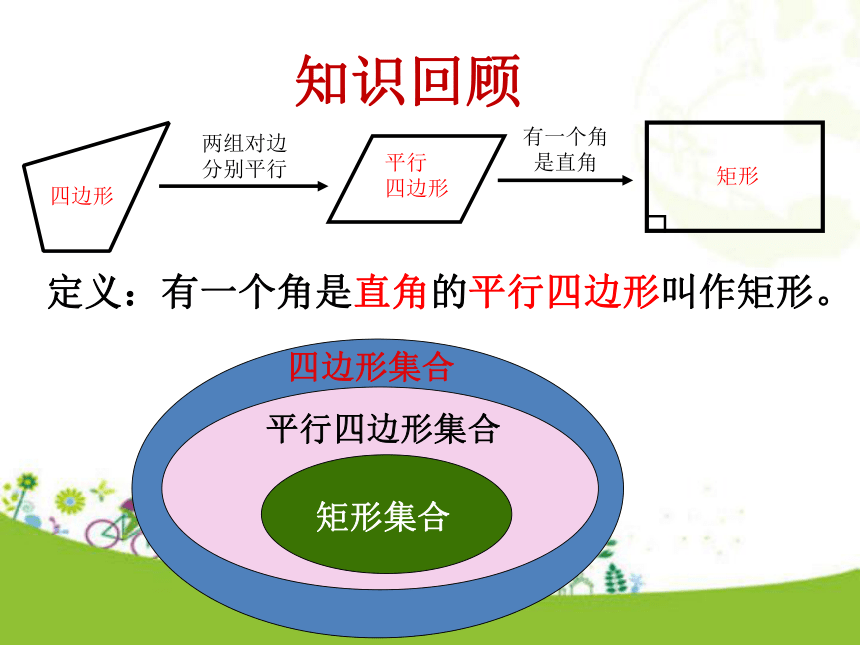
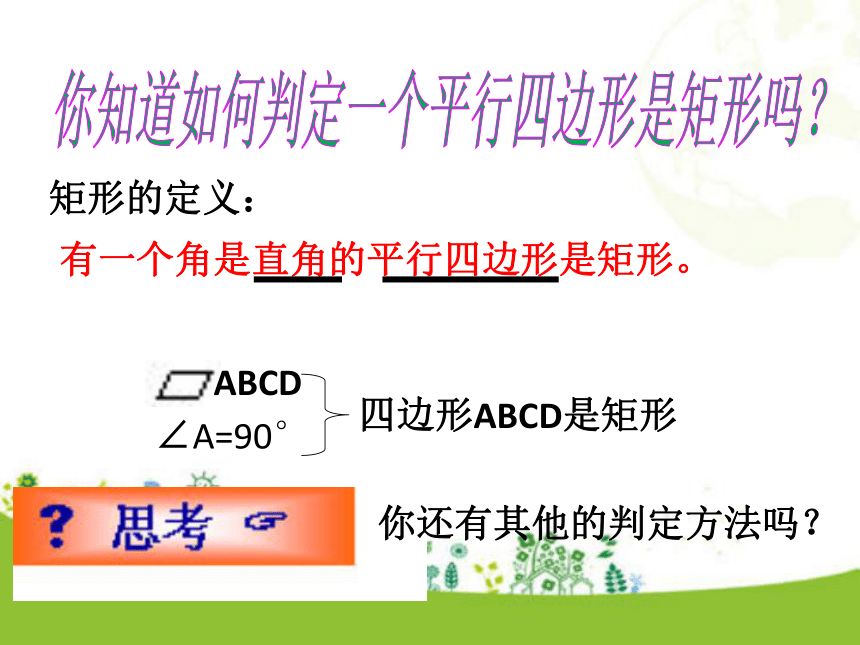
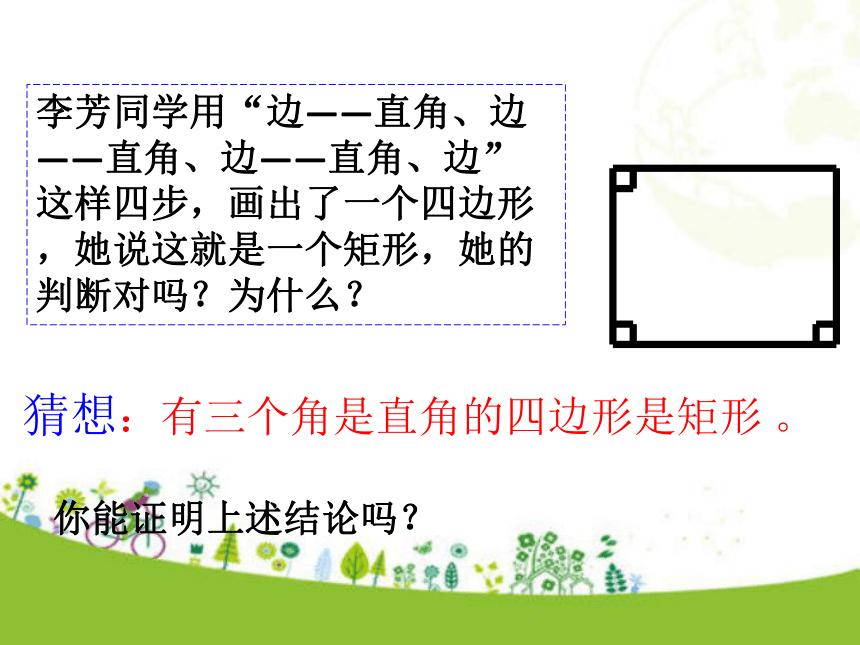
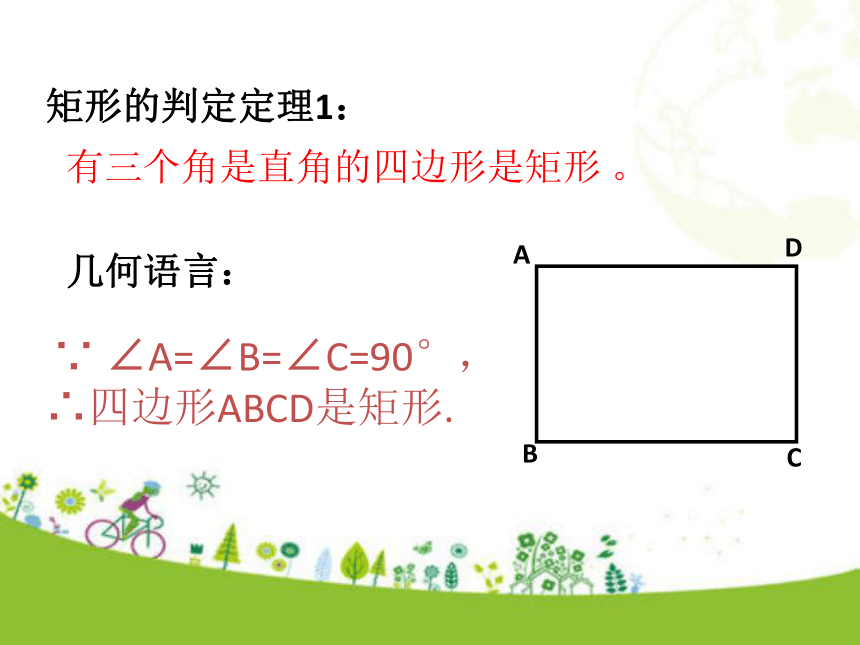
学习目标四边形定义:有一个角是直角的平行四边形叫作矩形。知识回顾你知道如何判定一个平行四边形是矩形吗?矩形的定义:有一个角是直角的平行四边形是矩形。你还有其他的判定方法吗?∠A=90°四边形ABCD是矩形李芳同学用“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?猜想:有三个角是直角的四边形是矩形 。你能证明上述结论吗?矩形的判定定理1:有三个角是直角的四边形是矩形 。 ∵ ∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.几何语言:工人师傅为了检验两组对边分别相等的四边形窗框是不是矩形,一种方法是量一量这个四边形的两条对角线的长度,如果两条对角线长相等,则窗框一定是矩形,你知道这是为什么吗?猜想:对角线相等的平行四边形是矩形 。你能证明上述结论吗?对角线相等的平行四边形是矩形 。矩形的判定定理2:几何语言:∵四边形ABCD是平行四边形,
AC=BD,∴四边形ABCD是矩形(对角线相等且互相平分的四边形是矩形。)(或OA=OC=OB=OD)下列条件中,不能判定四边形ABCD为矩形的是( ).
A.AB∥CD,AB=CD,AC=BD
B.∠A=∠B=∠D=90°
C.AB=BC,AD=CD,且∠C=90°
D.AB=CD,AD=BC,∠A=90°CC下列说法错误的是( )
A.有一个内角是直角的平行四边形是矩形
B.矩形的四个角都是直角,并且对角线相等
C.对角线相等的平行四边形是矩形
D.有两个角是直角的四边形是矩形如图, ABCD四个内角的平分线围成四边形EFGH,猜想四边形EFGH的形状,并说明理由。∵四边形ABCD是平行四边形, ∴∠DAB+∠ABC=180 °。证明:同理:∠EFG=90°,∠FGH=90°,∴四边形EFGH是矩形。∵AE,BE分别平分∠DAB,∠ABC , ∴∠EAB+∠EBA=90 °。∴∠AEB=90° ,即∠HEF=90°。下列说法正确的是 ( )
A.有一个角是直角的四边形是矩形
B.两条对角线相等的四边形是矩形
C.两条对角线垂直的四边形是矩形
D.四个角都是直角的四边形是矩形√如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角∠ACD的平分线于点F.
(1)求证:OE=OF.
(2)若CE=12,CF=5,求OC的长.
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
解:(1)证明:如图.
∵MN交∠ACB的平分线于点E,交∠ACB的外角∠ACD的平分线于点F,
∴∠2=∠5,∠4=∠6.
∵MN∥BC,∴∠1=∠5,∠3=∠6.
∴∠1=∠2,∠3=∠4.
∴OE=OC,OF=OC.∴OE=OF.
上运动到AC的中点时,四边形AECF是矩形.理由如下:
如图,连接AE,AF.
∵点O为AC的中点,∴OA=OC.
又∵OE=OF,∴四边形AECF是平行四边形.
∵∠ECF=90°,∴四边形AECF是矩形.
(江苏徐州中考)如图,在?ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E.连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠BOD= °时,四边形BECD是矩形.??小 结关于矩形的学习到此结束了,请你能总结一下矩形的性质有哪些?判定矩形的方法有哪些?谢谢!
2. 能综合利用矩形的性质与判定解决问题。
学习目标四边形定义:有一个角是直角的平行四边形叫作矩形。知识回顾你知道如何判定一个平行四边形是矩形吗?矩形的定义:有一个角是直角的平行四边形是矩形。你还有其他的判定方法吗?∠A=90°四边形ABCD是矩形李芳同学用“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?猜想:有三个角是直角的四边形是矩形 。你能证明上述结论吗?矩形的判定定理1:有三个角是直角的四边形是矩形 。 ∵ ∠A=∠B=∠C=90°,
∴四边形ABCD是矩形.几何语言:工人师傅为了检验两组对边分别相等的四边形窗框是不是矩形,一种方法是量一量这个四边形的两条对角线的长度,如果两条对角线长相等,则窗框一定是矩形,你知道这是为什么吗?猜想:对角线相等的平行四边形是矩形 。你能证明上述结论吗?对角线相等的平行四边形是矩形 。矩形的判定定理2:几何语言:∵四边形ABCD是平行四边形,
AC=BD,∴四边形ABCD是矩形(对角线相等且互相平分的四边形是矩形。)(或OA=OC=OB=OD)下列条件中,不能判定四边形ABCD为矩形的是( ).
A.AB∥CD,AB=CD,AC=BD
B.∠A=∠B=∠D=90°
C.AB=BC,AD=CD,且∠C=90°
D.AB=CD,AD=BC,∠A=90°CC下列说法错误的是( )
A.有一个内角是直角的平行四边形是矩形
B.矩形的四个角都是直角,并且对角线相等
C.对角线相等的平行四边形是矩形
D.有两个角是直角的四边形是矩形如图, ABCD四个内角的平分线围成四边形EFGH,猜想四边形EFGH的形状,并说明理由。∵四边形ABCD是平行四边形, ∴∠DAB+∠ABC=180 °。证明:同理:∠EFG=90°,∠FGH=90°,∴四边形EFGH是矩形。∵AE,BE分别平分∠DAB,∠ABC , ∴∠EAB+∠EBA=90 °。∴∠AEB=90° ,即∠HEF=90°。下列说法正确的是 ( )
A.有一个角是直角的四边形是矩形
B.两条对角线相等的四边形是矩形
C.两条对角线垂直的四边形是矩形
D.四个角都是直角的四边形是矩形√如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角∠ACD的平分线于点F.
(1)求证:OE=OF.
(2)若CE=12,CF=5,求OC的长.
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
解:(1)证明:如图.
∵MN交∠ACB的平分线于点E,交∠ACB的外角∠ACD的平分线于点F,
∴∠2=∠5,∠4=∠6.
∵MN∥BC,∴∠1=∠5,∠3=∠6.
∴∠1=∠2,∠3=∠4.
∴OE=OC,OF=OC.∴OE=OF.
上运动到AC的中点时,四边形AECF是矩形.理由如下:
如图,连接AE,AF.
∵点O为AC的中点,∴OA=OC.
又∵OE=OF,∴四边形AECF是平行四边形.
∵∠ECF=90°,∴四边形AECF是矩形.
(江苏徐州中考)如图,在?ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E.连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠BOD= °时,四边形BECD是矩形.??小 结关于矩形的学习到此结束了,请你能总结一下矩形的性质有哪些?判定矩形的方法有哪些?谢谢!
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
