青岛版数学八年级下册6.3 特殊的平行四边形(3菱形) 课件(18张ppt)
文档属性
| 名称 | 青岛版数学八年级下册6.3 特殊的平行四边形(3菱形) 课件(18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 00:00:00 | ||
图片预览





文档简介
课件18张PPT。6.3 特殊的平行四边形(3)青岛版数学八年级下册1.了解菱形的定义和性质。
2. 理解并会证明菱形的判定定理。
3.能综合利用菱形的性质和判定解决问题。
学习目标有一组邻边相等的平行四边形叫作菱形。菱形的定义是什么? 菱形的四条边都相等。
已知:如图,四边ABCD是菱形,
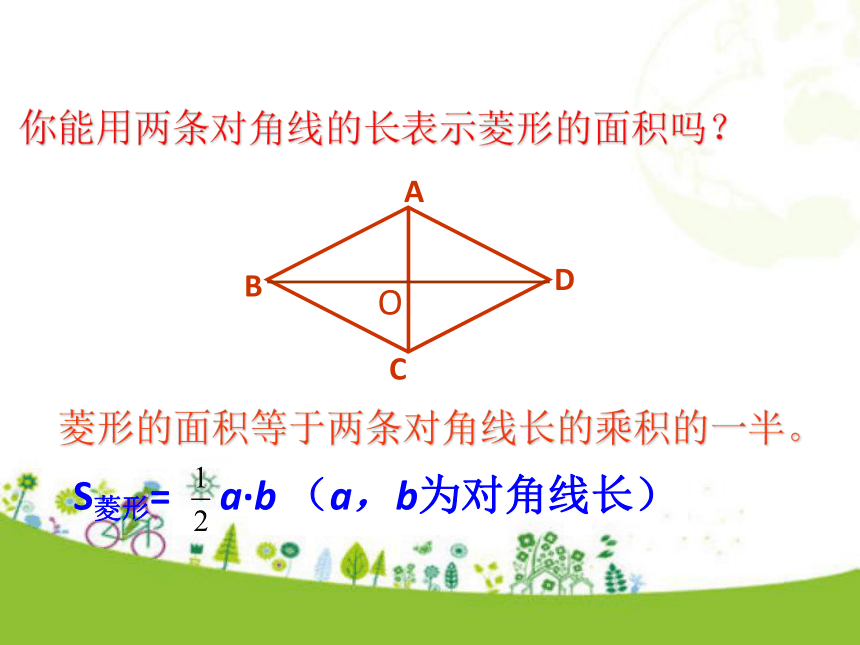
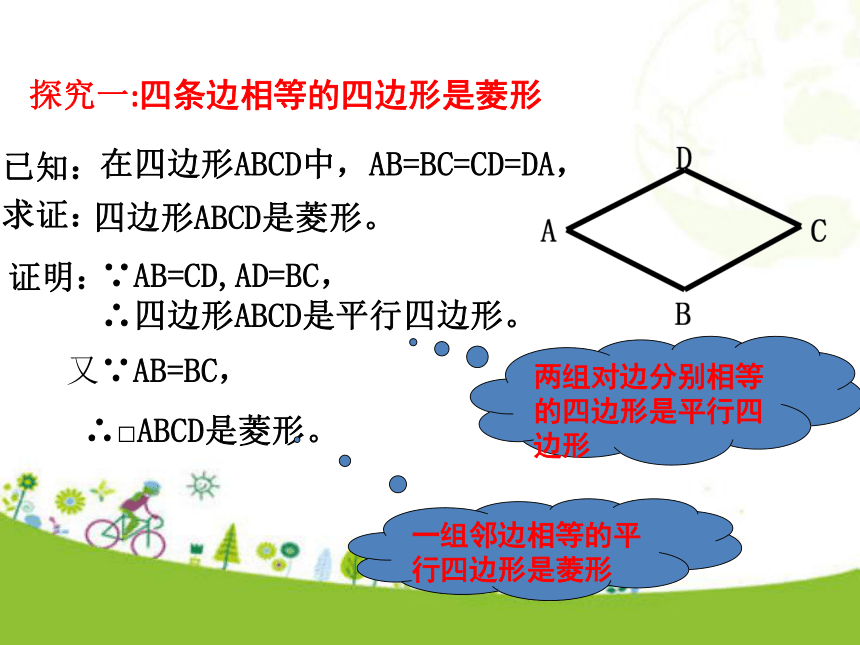
求证:AB=BC=CD=AD。性质定理1: 证明:∵四边形ABCD是菱形, ∴ AB=CD ,AD=BC (平行四边形的两组对边分别相等)。又∵AB=AD (菱形的定义),∴ AB=BC=CD=AD。性质定理2:已知:菱形ABCD的对角线AC和BD相交于点O,如图,证明:∵四边形ABCD是菱形,在△ABD中,∵BO=DO,∴AB=AD(菱形的四条边都相等)。∴AC⊥BD。求证:AC⊥BD 。 菱形的对角线互相垂直你能用两条对角线的长表示菱形的面积吗?菱形的面积等于两条对角线长的乘积的一半。S菱形= a·b (a,b为对角线长)探究一:四条边相等的四边形是菱形已知:求证:在四边形ABCD中,AB=BC=CD=DA,四边形ABCD是菱形。∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形。证明:两组对边分别相等的四边形是平行四边形又∵AB=BC,
∴□ABCD是菱形。一组邻边相等的平行四边形是菱形 菱形的判定定理1:
四条边相等的四边形是菱形几何语言:∴四边形ABCD是菱形。∵在四边形ABCD中,
AB=BC=CD=DA,探究二:对角线互相垂直的平行四边形是菱形已知:求证:在□ABCD中,AC,BD相交于点O, AC⊥BD。□ABCD是菱形。∵四边形ABCD是平行四边形,证明:垂直平分线的定义∵AC⊥BD,一组邻边相等的平行四边形是菱形∴BD垂直平分AC。∴OA=OC。∴AD=CD。∴□ABCD是菱形。 菱形的判定定理2:
对角线互相垂直的平行四边形是菱形几何语言:∴□ABCD是菱形。∵在□ABCD中,AC⊥BD,四边形菱形的判定方法及常见的判定思路四边形ABCD的对角线互相平分,要使它变为菱形,需要添加的条件是
四边形ABCD的对角线AC、BD互相垂直,则下列条件能判定四边形ABCD是菱形的条件是( )
A.BA=BC B.AC与BD互相平分
C.AC=BD D.AB∥CDBAB=BC或 AC⊥BD练 习·如图,在□ABCD中,对角线AC的垂直平分线EF交AD于点F,交BC于点E。
求证:四边形AECF是菱形。∵四边形ABCD是平行四边形, 又∵AF∥CE,
∴四边形AECF是平行四边形。
又∵ AC⊥EF,
∴四边形AECF是菱形。证明:∴AD∥BC即AF∥CE。∴∠1= ∠2。∵EF垂直平分AC,∴OA=OC。在△AOF和△COE中,∠1=∠2,OA=OC,∠AOF=∠COE,∴ △AOF≌△COE(ASA)。∴AF=CE。如图,△ABC为等腰三角形,把它沿底边BC翻折后,得△DBC.请你判断四边形ABDC的形状,并说出你的理由。 解:四边形ABDC是菱形。理由如下:
∵△ABC为等腰三角形, BC为底边,
∴AB=AC。
由折叠可知:AB=BD,AC=CD。
∴AB=BD=AC=CD。
∴四边形ABDC是菱形。四条边都相等的四边形是菱形如图,点O是矩形ABCD对角线的交点,DE∥AC,CE∥BD,DE和CE相交于E。
求证:四边形OCED是菱形。证明:∵四边形ABCD是矩形,
∴AC=BD,OC= AC,OD= BD。
∴OC=OD。
∵ DE∥AC,CE∥BD,
∴四边形OCED是平行四边形。
又∵ OC=OD,
∴四边形OCED是菱形。一组邻边相等的平行四边形叫作菱形如图,□ABCD的两条对角线AC ,BD 相交于点O,AB=5,AC=6,BD=8。
求证:四边形ABCD是菱形。证明:∵四边形ABCD是平行四边形,
∴OA=OC= AC=3,OB=OD= BD=4。
∵OA2+OB2=32+42=25,AB2=52=25,
∴OA2+OB2=AB2。
∴△AOB是直角三角形,∠AOB=90°。
∴AC⊥BD。
又∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形。小 结请同学们总结一下菱形的性质与判定定理谢谢!
2. 理解并会证明菱形的判定定理。
3.能综合利用菱形的性质和判定解决问题。
学习目标有一组邻边相等的平行四边形叫作菱形。菱形的定义是什么? 菱形的四条边都相等。
已知:如图,四边ABCD是菱形,
求证:AB=BC=CD=AD。性质定理1: 证明:∵四边形ABCD是菱形, ∴ AB=CD ,AD=BC (平行四边形的两组对边分别相等)。又∵AB=AD (菱形的定义),∴ AB=BC=CD=AD。性质定理2:已知:菱形ABCD的对角线AC和BD相交于点O,如图,证明:∵四边形ABCD是菱形,在△ABD中,∵BO=DO,∴AB=AD(菱形的四条边都相等)。∴AC⊥BD。求证:AC⊥BD 。 菱形的对角线互相垂直你能用两条对角线的长表示菱形的面积吗?菱形的面积等于两条对角线长的乘积的一半。S菱形= a·b (a,b为对角线长)探究一:四条边相等的四边形是菱形已知:求证:在四边形ABCD中,AB=BC=CD=DA,四边形ABCD是菱形。∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形。证明:两组对边分别相等的四边形是平行四边形又∵AB=BC,
∴□ABCD是菱形。一组邻边相等的平行四边形是菱形 菱形的判定定理1:
四条边相等的四边形是菱形几何语言:∴四边形ABCD是菱形。∵在四边形ABCD中,
AB=BC=CD=DA,探究二:对角线互相垂直的平行四边形是菱形已知:求证:在□ABCD中,AC,BD相交于点O, AC⊥BD。□ABCD是菱形。∵四边形ABCD是平行四边形,证明:垂直平分线的定义∵AC⊥BD,一组邻边相等的平行四边形是菱形∴BD垂直平分AC。∴OA=OC。∴AD=CD。∴□ABCD是菱形。 菱形的判定定理2:
对角线互相垂直的平行四边形是菱形几何语言:∴□ABCD是菱形。∵在□ABCD中,AC⊥BD,四边形菱形的判定方法及常见的判定思路四边形ABCD的对角线互相平分,要使它变为菱形,需要添加的条件是
四边形ABCD的对角线AC、BD互相垂直,则下列条件能判定四边形ABCD是菱形的条件是( )
A.BA=BC B.AC与BD互相平分
C.AC=BD D.AB∥CDBAB=BC或 AC⊥BD练 习·如图,在□ABCD中,对角线AC的垂直平分线EF交AD于点F,交BC于点E。
求证:四边形AECF是菱形。∵四边形ABCD是平行四边形, 又∵AF∥CE,
∴四边形AECF是平行四边形。
又∵ AC⊥EF,
∴四边形AECF是菱形。证明:∴AD∥BC即AF∥CE。∴∠1= ∠2。∵EF垂直平分AC,∴OA=OC。在△AOF和△COE中,∠1=∠2,OA=OC,∠AOF=∠COE,∴ △AOF≌△COE(ASA)。∴AF=CE。如图,△ABC为等腰三角形,把它沿底边BC翻折后,得△DBC.请你判断四边形ABDC的形状,并说出你的理由。 解:四边形ABDC是菱形。理由如下:
∵△ABC为等腰三角形, BC为底边,
∴AB=AC。
由折叠可知:AB=BD,AC=CD。
∴AB=BD=AC=CD。
∴四边形ABDC是菱形。四条边都相等的四边形是菱形如图,点O是矩形ABCD对角线的交点,DE∥AC,CE∥BD,DE和CE相交于E。
求证:四边形OCED是菱形。证明:∵四边形ABCD是矩形,
∴AC=BD,OC= AC,OD= BD。
∴OC=OD。
∵ DE∥AC,CE∥BD,
∴四边形OCED是平行四边形。
又∵ OC=OD,
∴四边形OCED是菱形。一组邻边相等的平行四边形叫作菱形如图,□ABCD的两条对角线AC ,BD 相交于点O,AB=5,AC=6,BD=8。
求证:四边形ABCD是菱形。证明:∵四边形ABCD是平行四边形,
∴OA=OC= AC=3,OB=OD= BD=4。
∵OA2+OB2=32+42=25,AB2=52=25,
∴OA2+OB2=AB2。
∴△AOB是直角三角形,∠AOB=90°。
∴AC⊥BD。
又∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形。小 结请同学们总结一下菱形的性质与判定定理谢谢!
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
