高中数学北师大版必修3第一章统计第二节抽样方法2.2分层抽样与系统抽样教学课件 (共15张PPT)
文档属性
| 名称 | 高中数学北师大版必修3第一章统计第二节抽样方法2.2分层抽样与系统抽样教学课件 (共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 22:09:05 | ||
图片预览






文档简介
(共15张PPT)
2.2.1 分层抽样
北师大版必修3
那么当总体中的个体有很大差异时,适宜采用什么抽取方法?
问题1:全国各地的人口和住户的基本情况相同吗?
不同,有很大的差异
问题2:如果用简单随机抽样或系统抽样来抽取,样本具有代表性吗?
不具有代表性
提出问题
1、若采用简单随机抽样,样本的组成会出现什么情况?
2、所抽出的样本中什么因素会对样本的平均身高产生重大影响?
3、你将如何抽取?为什么?
为了估测高二某班全体学生(共有50人,其中男生30人,女生20人)的平均身高,现想从班级学生中抽取出容量为10的样本进行调查。
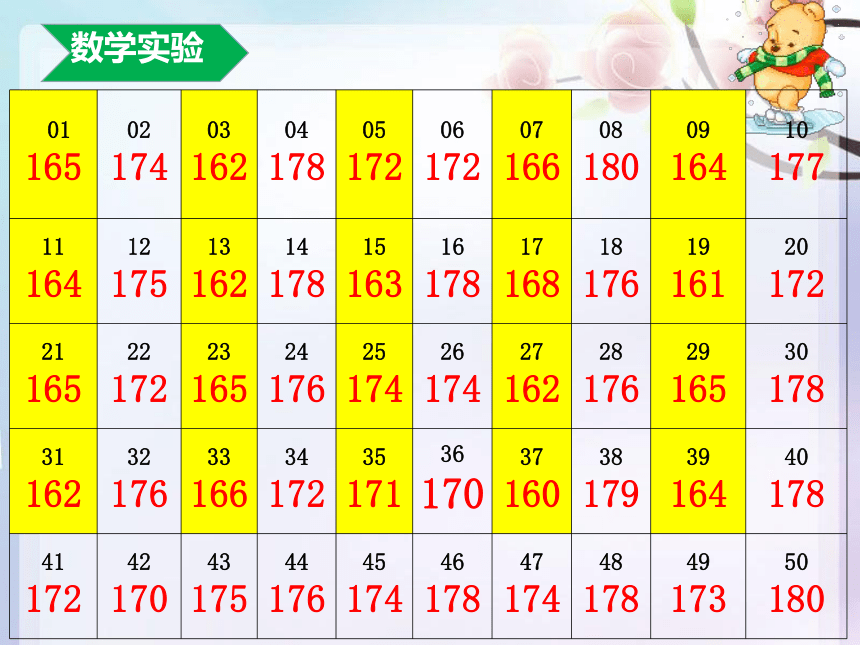
数学实验
01 165 02 174 03 162 04 178 05 172 06 172 07 166 08 180 09 164 10 177
11 164 12 175 13 162 14 178 15 163 16 178 17 168 18 176 19 161 20 172
21 165 22 172 23 165 24 176 25 174 26 174 27 162 28 176 29 165 30 178
31 162 32 176 33 166 34 172 35 171 36 170 37 160 38 179 39 164 40 178
41 172 42 170 43 175 44 176 45 174 46 178 47 174 48 178 49 173 50 180
数学实验
数学建构
分 层 抽 样 的 定 义
1
2
3
4
适用范围:总体中个体差异明显
目的:使样本能客观的反映总体情况
原则:分成”层次分明”的几个部分
特点:按各部分在总体中所占比例实施抽样
分层抽样的具体抽样的步骤:
(1) 将总体按一定的标准分层(分层)
(2)总体与样本容量确定抽取的比例(定比)
(3) 确定各层抽取的样本数(定量)
(4)在每一层进行抽样(可用简单随机抽样或系统抽样)(抽样)
数学建构
数学应用
例1、某电视台在因特网上就观众对某一节目的喜爱程度进行调查,参加调查的总人数为12000人,其中持各种态度的人数如表所示:
很喜爱 喜爱 一般 不喜欢
2435 4567 3926 1072
电视台为了进一步了解观众的具体想法和意见,打算从中抽取60人进行更为详细的调查,应怎样进行抽样?
1. 在下列问题中,各采用什么抽样方法抽取样本较为合适?
(1)从20台彩电中抽取4台进行质量检验;
(2)科学会堂有32排座位,每排有40各座位(座位号为01~40),一次报告会坐满了听众,会后为了听取意见,留下了座位号为18的所有的32名听众进行座谈;
(3)实验中学有180名教工,其中有专职教师144名,管理人员12名,后勤服务人员24人,今从中抽取一个容量15的样本。
简单随机抽样法
系统抽样法
分层抽样法
数学应用
方法
类别 共同
特点 抽样特征 相互联系 适应范围
简单随
机抽样
系统
抽样
分层
抽样
抽样过程中每个个体被抽取的可能性相等
将总体分成均衡几部分,按规则在各段抽取
将总体分成互不交叉的几层,按比例分层抽样
用简单随机抽样抽取起始号码
总体中的个体数较少
总体中的个体数较多
总体由差异明显的几部分组成
从总体中逐个不放回抽取
用简单随机抽样或系统抽样对各层抽样
数学提升
1. 某学校有职工140人,其中教师91人,教辅人员28人,总务后勤人员21人,为了解职工的某种情况,要从中抽取一个容量为20的样本,则应抽取的教师、教辅人员、总务后勤的人数分别为 、 、 。
13
4
3
2、 假设某地区有高中生2 400人,初中生10 900人,小学生11 000人.此地区教育部门为了了解本地区中小学生的近视情况及其形成原因,要从本地区的中小学生中抽取1%的学生进行调查,你认为应当怎样抽取样本?
课堂检测
1、分层抽样的概念、特征和步骤
2、三种抽样方法相互之间的区别与联系
课堂小结
课后作业
优化设计--课时训练P3 1-9题
谢谢大家
2.2.1 分层抽样
北师大版必修3
那么当总体中的个体有很大差异时,适宜采用什么抽取方法?
问题1:全国各地的人口和住户的基本情况相同吗?
不同,有很大的差异
问题2:如果用简单随机抽样或系统抽样来抽取,样本具有代表性吗?
不具有代表性
提出问题
1、若采用简单随机抽样,样本的组成会出现什么情况?
2、所抽出的样本中什么因素会对样本的平均身高产生重大影响?
3、你将如何抽取?为什么?
为了估测高二某班全体学生(共有50人,其中男生30人,女生20人)的平均身高,现想从班级学生中抽取出容量为10的样本进行调查。
数学实验
01 165 02 174 03 162 04 178 05 172 06 172 07 166 08 180 09 164 10 177
11 164 12 175 13 162 14 178 15 163 16 178 17 168 18 176 19 161 20 172
21 165 22 172 23 165 24 176 25 174 26 174 27 162 28 176 29 165 30 178
31 162 32 176 33 166 34 172 35 171 36 170 37 160 38 179 39 164 40 178
41 172 42 170 43 175 44 176 45 174 46 178 47 174 48 178 49 173 50 180
数学实验
数学建构
分 层 抽 样 的 定 义
1
2
3
4
适用范围:总体中个体差异明显
目的:使样本能客观的反映总体情况
原则:分成”层次分明”的几个部分
特点:按各部分在总体中所占比例实施抽样
分层抽样的具体抽样的步骤:
(1) 将总体按一定的标准分层(分层)
(2)总体与样本容量确定抽取的比例(定比)
(3) 确定各层抽取的样本数(定量)
(4)在每一层进行抽样(可用简单随机抽样或系统抽样)(抽样)
数学建构
数学应用
例1、某电视台在因特网上就观众对某一节目的喜爱程度进行调查,参加调查的总人数为12000人,其中持各种态度的人数如表所示:
很喜爱 喜爱 一般 不喜欢
2435 4567 3926 1072
电视台为了进一步了解观众的具体想法和意见,打算从中抽取60人进行更为详细的调查,应怎样进行抽样?
1. 在下列问题中,各采用什么抽样方法抽取样本较为合适?
(1)从20台彩电中抽取4台进行质量检验;
(2)科学会堂有32排座位,每排有40各座位(座位号为01~40),一次报告会坐满了听众,会后为了听取意见,留下了座位号为18的所有的32名听众进行座谈;
(3)实验中学有180名教工,其中有专职教师144名,管理人员12名,后勤服务人员24人,今从中抽取一个容量15的样本。
简单随机抽样法
系统抽样法
分层抽样法
数学应用
方法
类别 共同
特点 抽样特征 相互联系 适应范围
简单随
机抽样
系统
抽样
分层
抽样
抽样过程中每个个体被抽取的可能性相等
将总体分成均衡几部分,按规则在各段抽取
将总体分成互不交叉的几层,按比例分层抽样
用简单随机抽样抽取起始号码
总体中的个体数较少
总体中的个体数较多
总体由差异明显的几部分组成
从总体中逐个不放回抽取
用简单随机抽样或系统抽样对各层抽样
数学提升
1. 某学校有职工140人,其中教师91人,教辅人员28人,总务后勤人员21人,为了解职工的某种情况,要从中抽取一个容量为20的样本,则应抽取的教师、教辅人员、总务后勤的人数分别为 、 、 。
13
4
3
2、 假设某地区有高中生2 400人,初中生10 900人,小学生11 000人.此地区教育部门为了了解本地区中小学生的近视情况及其形成原因,要从本地区的中小学生中抽取1%的学生进行调查,你认为应当怎样抽取样本?
课堂检测
1、分层抽样的概念、特征和步骤
2、三种抽样方法相互之间的区别与联系
课堂小结
课后作业
优化设计--课时训练P3 1-9题
谢谢大家
