高中数学人教B版(2019)必修(第三册)7.3.4正切函数的性质与图像课件(共35张PPT)
文档属性
| 名称 | 高中数学人教B版(2019)必修(第三册)7.3.4正切函数的性质与图像课件(共35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 00:00:00 | ||
图片预览









文档简介
(共35张PPT)
数学使人聪颖
数学使人严谨??
数学使人深刻?
? ? 数学使人缜密???
数学使人坚毅?
?? 数学使人智慧???
-
-
1
-1
-
-
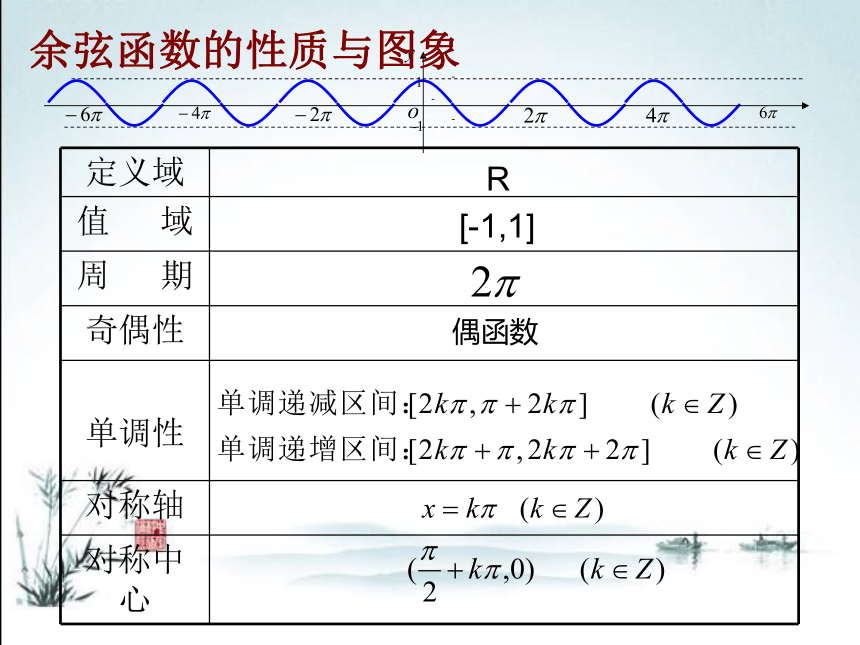
定义域
值 域
周 期
奇偶性
单调性
对称轴
对称中心
R
[-1,1]
偶函数
余弦函数的性质与图象
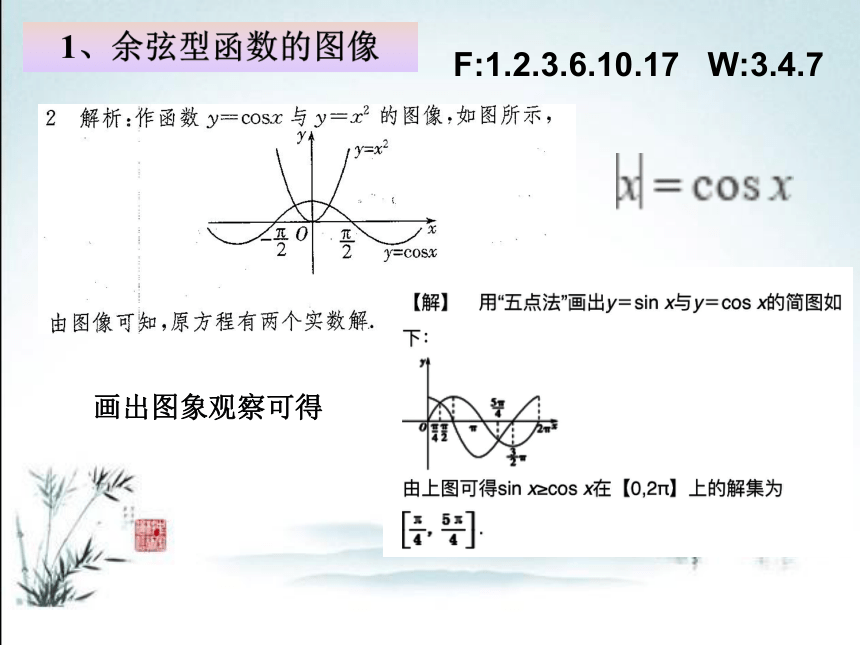
1、余弦型函数的图像
F:1.2.3.6.10.17 W:3.4.7
画出图象观察可得
2、余弦型函数的奇偶性与周期性
F:4.5.6.11.16 W:2.5.6.9
3、余弦型函数的单调性
F:6.7.10.12.15 W:6.7
4、余弦型函数的值域和最大(小)值
F:8.9 .18 W:2.5.6.9
思考:
类比正弦型函数 的性质,
你能总结出正切型函数 的性质吗?
函数
定义域
值域
周期性
奇偶性
对称性
单调性
正切函数的图象和性质
1、掌握画正切函数图象的方法
2、归纳正切函数性质并能简单应用
3、感悟思想方法,体会数学学习的快乐
我们的目标
数形结合、整体代换、类比
1.角 的正切的定义:
2.正切函数的定义:
因变量
自变量
温故知新 推陈出新
O
y
x
A
P(x,y)
2、周期性
tan(x+π)=tanx,x∈R,x≠π/2+kπ,k∈Z
正切函数是周期函数,周期T= π
1、正切函数定义域
3、奇偶性
tan(-x)=-tanx,x∈R,x≠π/2+kπ ,k∈Z
正切函数是奇函数,原点(0,0)是其对称中心
一、正切函数的性质
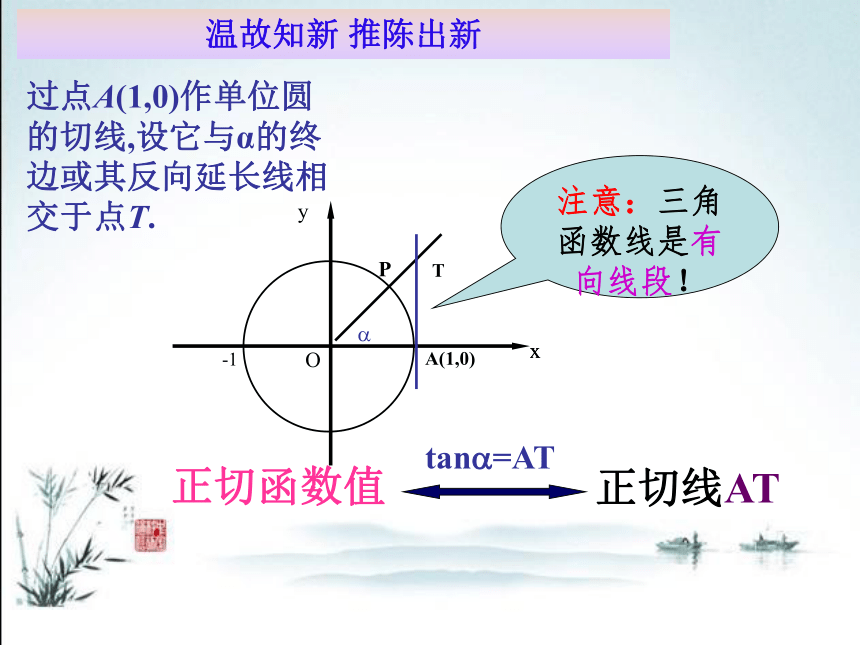
正切函数值
y
x
x
O
-1
?
P
A(1,0)
T
tan?=AT
正切线AT
注意:三角函数线是有向线段!
过点A(1,0)作单位圆的切线,设它与α的终边或其反向延长线相交于点T.
温故知新 推陈出新
M
x
y
O
P
α的终边
A(1,0)
(Ⅰ)
T
M
x
y
O
P
α的终边
A(1,0)
(Ⅳ)
T
M
x
y
O
P
α的终边
A(1,0)
(Ⅱ)
T
M
x
y
O
P
α的终边
A(1,0)
(Ⅲ)
T
正切函数在每一个开区间
内都是增函数。
5、值域
4、单调性
正切函数的值域是实数集R.
我当设计师
请你自己设计一个方案
作出正切函数y=tanx的图象
二、正切函数的图象
1、根据正切函数的定义域和周期,
取 x∈ (-π/2,π/2) ,先画函数y=tanx 在
(-π/2,π/2)一个周期上的图象 。
作法:
(1) 等分:
(2) 作正切线
(3) 平移
(4) 连线
把单位圆右半圆分成8等份。
,
,
,
,
,
利用正切线画出函数 , 的图像:
null
正切函数的图象
由无穷多支曲线组成,
由直线 隔开
0
三点两线作图:
2、 把y=tanx,x∈ (-π/2,π/2)图象向左或者
向右平移,每次平移π个单位长度就得到y=tanx
x∈R,且x≠π/2+kπ,k∈Z 的图象。
O
y
x
1
-1
正切函数的图象叫正切曲线,其特征是:
1、被相互平行的直线 x=π/2+kπ,k∈Z
所隔开的无穷多支曲线组成的。
根据函数图象,分析正切函数的性质
正弦函数y=tanx的性质
定义域
值域
周期
奇偶性
单调性
对称性
R
奇函数
在
开区间内都是增函数。
(1)正切函数是整个定义域上的增函数吗?为什么?
(2)正切函数会不会在某一区间内是减函数?为什么?
问题:
A
B
在每一个开区间
, 内都是增函数。
问 题 讨 论
正切函数值无边
图象限于直线间
飞引三个定型点
扶摇直上九重天
学以致用
例题1
整体代换
整体代换思想还可以应用于求解正切函数的那些性质,你能给大家编写几道题吗?
我来做老师
求下列函数的周期:
由上面两例,你能得到函数y=Atan(ωx+Ф)的周期吗
定义法求周期
例题2
公式法求周期
存在非零常数T,任取定义域内x,满足f(x+T)=f(x)
例题3
比较 与 的大小.
解:
且 内单调递增,
0
y
x
null
例题巩固
利用正切函数的单调性比较两个正切值的大小
解题小贴士
利用正切函数单调性比较大小的步骤:
?利用诱导公式将角转到同一单调区间内,通常是化到区间
或 内.
?运用单调性比较大小.
求x的取值集合
1.
练一练
2.
0
求函数 的定义域、周期和单调区间。
解:原函数要有意义,自变量x应满足
即
所以,原函数的定义域是
所以原函数的周期是2.
由
解得
所以原函数的单调递增区间是
例题4
(1)正切函数的图像
(2)正切函数的性质:
定义域:
值域:
周期性:
奇偶性:
单调性:
对称性:
全体实数R
正切函数是周期函数,最小正周期T=
奇函数,
正切函数在开区间
内都是增函数。
小结
0
-1
1
x
y
对称中心: 无对称轴
牛刀小试
对称中心及周期
2.
解 :
值域 : R
∵tant的对称中心( ,0),
对称中心及周期
2.
分层作业:
A:课后练基础篇+分层13
B:课后练基础篇+提升篇+分层13
Thank You !
数学使人聪颖
数学使人严谨??
数学使人深刻?
? ? 数学使人缜密???
数学使人坚毅?
?? 数学使人智慧???
-
-
1
-1
-
-
定义域
值 域
周 期
奇偶性
单调性
对称轴
对称中心
R
[-1,1]
偶函数
余弦函数的性质与图象
1、余弦型函数的图像
F:1.2.3.6.10.17 W:3.4.7
画出图象观察可得
2、余弦型函数的奇偶性与周期性
F:4.5.6.11.16 W:2.5.6.9
3、余弦型函数的单调性
F:6.7.10.12.15 W:6.7
4、余弦型函数的值域和最大(小)值
F:8.9 .18 W:2.5.6.9
思考:
类比正弦型函数 的性质,
你能总结出正切型函数 的性质吗?
函数
定义域
值域
周期性
奇偶性
对称性
单调性
正切函数的图象和性质
1、掌握画正切函数图象的方法
2、归纳正切函数性质并能简单应用
3、感悟思想方法,体会数学学习的快乐
我们的目标
数形结合、整体代换、类比
1.角 的正切的定义:
2.正切函数的定义:
因变量
自变量
温故知新 推陈出新
O
y
x
A
P(x,y)
2、周期性
tan(x+π)=tanx,x∈R,x≠π/2+kπ,k∈Z
正切函数是周期函数,周期T= π
1、正切函数定义域
3、奇偶性
tan(-x)=-tanx,x∈R,x≠π/2+kπ ,k∈Z
正切函数是奇函数,原点(0,0)是其对称中心
一、正切函数的性质
正切函数值
y
x
x
O
-1
?
P
A(1,0)
T
tan?=AT
正切线AT
注意:三角函数线是有向线段!
过点A(1,0)作单位圆的切线,设它与α的终边或其反向延长线相交于点T.
温故知新 推陈出新
M
x
y
O
P
α的终边
A(1,0)
(Ⅰ)
T
M
x
y
O
P
α的终边
A(1,0)
(Ⅳ)
T
M
x
y
O
P
α的终边
A(1,0)
(Ⅱ)
T
M
x
y
O
P
α的终边
A(1,0)
(Ⅲ)
T
正切函数在每一个开区间
内都是增函数。
5、值域
4、单调性
正切函数的值域是实数集R.
我当设计师
请你自己设计一个方案
作出正切函数y=tanx的图象
二、正切函数的图象
1、根据正切函数的定义域和周期,
取 x∈ (-π/2,π/2) ,先画函数y=tanx 在
(-π/2,π/2)一个周期上的图象 。
作法:
(1) 等分:
(2) 作正切线
(3) 平移
(4) 连线
把单位圆右半圆分成8等份。
,
,
,
,
,
利用正切线画出函数 , 的图像:
null
正切函数的图象
由无穷多支曲线组成,
由直线 隔开
0
三点两线作图:
2、 把y=tanx,x∈ (-π/2,π/2)图象向左或者
向右平移,每次平移π个单位长度就得到y=tanx
x∈R,且x≠π/2+kπ,k∈Z 的图象。
O
y
x
1
-1
正切函数的图象叫正切曲线,其特征是:
1、被相互平行的直线 x=π/2+kπ,k∈Z
所隔开的无穷多支曲线组成的。
根据函数图象,分析正切函数的性质
正弦函数y=tanx的性质
定义域
值域
周期
奇偶性
单调性
对称性
R
奇函数
在
开区间内都是增函数。
(1)正切函数是整个定义域上的增函数吗?为什么?
(2)正切函数会不会在某一区间内是减函数?为什么?
问题:
A
B
在每一个开区间
, 内都是增函数。
问 题 讨 论
正切函数值无边
图象限于直线间
飞引三个定型点
扶摇直上九重天
学以致用
例题1
整体代换
整体代换思想还可以应用于求解正切函数的那些性质,你能给大家编写几道题吗?
我来做老师
求下列函数的周期:
由上面两例,你能得到函数y=Atan(ωx+Ф)的周期吗
定义法求周期
例题2
公式法求周期
存在非零常数T,任取定义域内x,满足f(x+T)=f(x)
例题3
比较 与 的大小.
解:
且 内单调递增,
0
y
x
null
例题巩固
利用正切函数的单调性比较两个正切值的大小
解题小贴士
利用正切函数单调性比较大小的步骤:
?利用诱导公式将角转到同一单调区间内,通常是化到区间
或 内.
?运用单调性比较大小.
求x的取值集合
1.
练一练
2.
0
求函数 的定义域、周期和单调区间。
解:原函数要有意义,自变量x应满足
即
所以,原函数的定义域是
所以原函数的周期是2.
由
解得
所以原函数的单调递增区间是
例题4
(1)正切函数的图像
(2)正切函数的性质:
定义域:
值域:
周期性:
奇偶性:
单调性:
对称性:
全体实数R
正切函数是周期函数,最小正周期T=
奇函数,
正切函数在开区间
内都是增函数。
小结
0
-1
1
x
y
对称中心: 无对称轴
牛刀小试
对称中心及周期
2.
解 :
值域 : R
∵tant的对称中心( ,0),
对称中心及周期
2.
分层作业:
A:课后练基础篇+分层13
B:课后练基础篇+提升篇+分层13
Thank You !
