人教版九年级数学下册28.2.1 解直角三角形课件(共24张PPT)
文档属性
| 名称 | 人教版九年级数学下册28.2.1 解直角三角形课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 187.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 08:29:02 | ||
图片预览




文档简介
课件24张PPT。
人教版 九年级数学下册
第28章 锐角三角函数
28.2.1 解直角三角形
学习目标1. 了解并掌握解直角三角形的概念;
2. 理解直角三角形中的五个元素之间的联系. (重点)
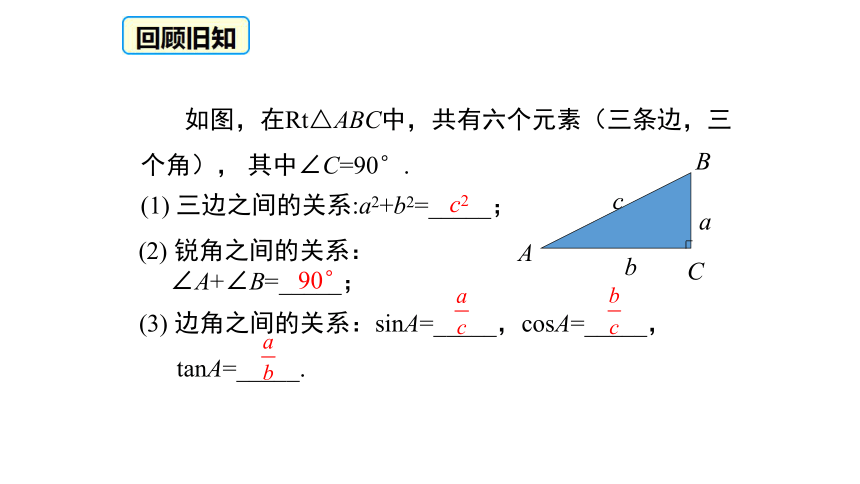
3. 学会解直角三角形. (难点)(1) 三边之间的关系:a2+b2=_____;(2) 锐角之间的关系:
∠A+∠B=_____;(3) 边角之间的关系:sinA=_____,cosA=_____,
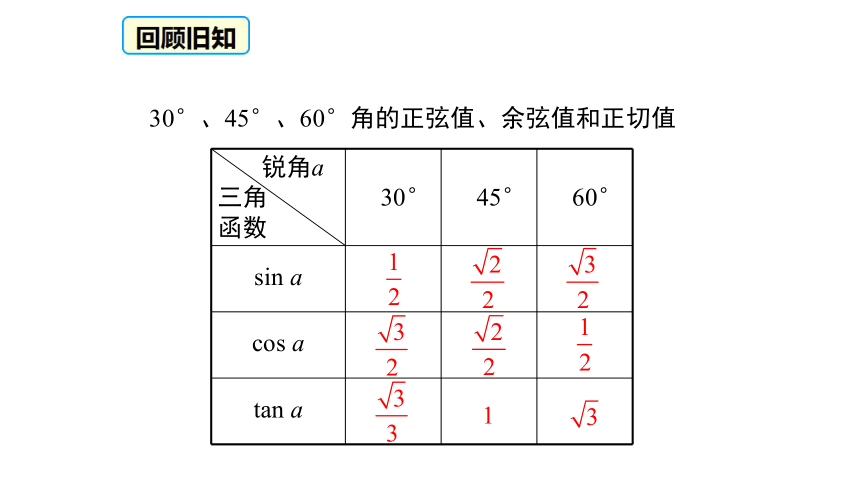
tanA=_____. 如图,在Rt△ABC中,共有六个元素(三条边,三个角), 其中∠C=90°.c290°30°、45°、60°角的正弦值、余弦值和正切值1新知探究 在直角三角形中,除直角外,共有五个元素,即三条边和两个锐角。
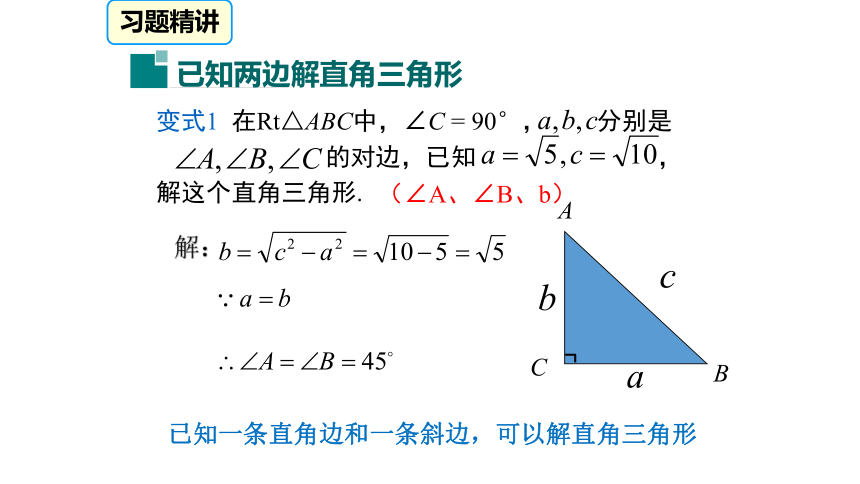
由直角三角形中的已知元素,求出其余未知元素的过程,叫作解直角三角形.新知探究(∠A、∠B、AB)已知两条直角边,可以解直角三角形习题精讲变式1 在Rt△ABC中,∠C = 90°, 分别是
的对边,已知 ,
解这个直角三角形.解:(∠A、∠B、b)已知一条直角边和一条斜边,可以解直角三角形习题精讲变式2 在Rt△ABC中,∠C = 90°, 分别是
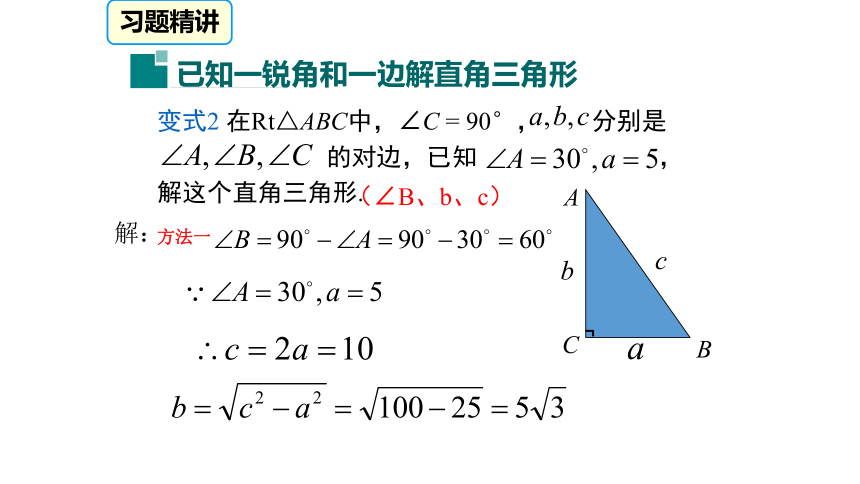
的对边,已知 ,
解这个直角三角形.
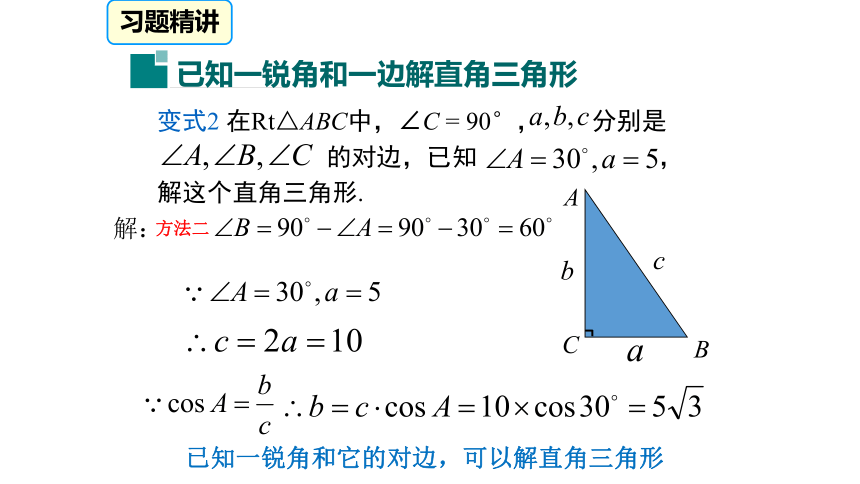
解:方法一(∠B、b、c)习题精讲变式2 在Rt△ABC中,∠C = 90°, 分别是
的对边,已知 ,
解这个直角三角形.
解:方法二已知一锐角和它的对边,可以解直角三角形习题精讲变式3 在Rt△ABC中,∠C = 90°, 分别是
的对边,已知 ,
解这个直角三角形.解:方法一(∠A、b、c)习题精讲变式3 在Rt△ABC中,∠C = 90°, 分别是
的对边,已知 ,
解这个直角三角形.解:方法二习题精讲变式3 在Rt△ABC中,∠C = 90°, 分别是
的对边,已知 ,
解这个直角三角形.解:方法三已知一锐角和它的邻边,可以解直角三角形习题精讲变式4 在Rt△ABC中, , 分别是
的对边,已知 ,
解这个直角三角形.解:方法一方法二(∠A、a、b)已知一锐角和斜边,可以解直角三角形新知探究已知两角能否解直角三角形? 归纳总结解直角三角形必备条件已知两边解直角三角形已知一个锐角和一边解直角三角形只要知道五个元素中的两个元素 就可以求出余下的三个未知元素(至少有一个是边)针对训练 在Rt△ABC中,有下列情况,则直角三角形可解的是( )
A.已知
B.已知
C.已知
D.已知D生活中的数学设塔顶中心点为B,塔身中心线与垂直中心线的夹角为∠ A,过B点向垂直中心线引垂线,垂足为点C(如图),在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m.问:倾斜角∠A是多少?所以∠A≈5.48°ABC解:新知探究例2 如图,在Rt△ABC中,∠C=90°,∠B=35°,b=20,解这个直角三角形 (结果保留小数点后一位).跟踪训练 在 Rt△ABC 中,∠C=90°,∠B=72°,c = 14.
根据条件解直角三角形.
( 参考数据: )解:课堂小结解直角三角形依据只要知道五个元素中的两个元素(至少有一个是边),就可以求出余下的三个未知元素勾股定理两锐角互余锐角三角函数已知斜边求直边,正弦余弦很方便;
已知直边求直边,正切余切理当然;
已知两边求一角,函数关系要选好;
已知两边求一边,勾股定理最方便;
已知锐角求锐角,互余关系要记好;
已知直边求斜边,用除还需正余弦;
计算方法要选择,能用乘法不用除.优选关系式家庭作业1. 如图,在Rt△ABC中,∠C=90°,∠B=30°,
AB=8,则BC的长是 ( )2. 在Rt△ABC中,∠C=90°,∠B=37°,BC=32,则
AC = (参考数据:sin37°≈0.60,cos37°≈0.80,
tan37°≈0.75).家庭作业3. 在Rt△ABC 中, ,
,根据下列条件解直角三角形:
(1)
(2)
(3) 家庭作业【选做】 如图,在Rt△ABC 中,∠C=90°,cosA = ,
BC = 5, 试求AB的长.
人教版 九年级数学下册
第28章 锐角三角函数
28.2.1 解直角三角形
学习目标1. 了解并掌握解直角三角形的概念;
2. 理解直角三角形中的五个元素之间的联系. (重点)
3. 学会解直角三角形. (难点)(1) 三边之间的关系:a2+b2=_____;(2) 锐角之间的关系:
∠A+∠B=_____;(3) 边角之间的关系:sinA=_____,cosA=_____,
tanA=_____. 如图,在Rt△ABC中,共有六个元素(三条边,三个角), 其中∠C=90°.c290°30°、45°、60°角的正弦值、余弦值和正切值1新知探究 在直角三角形中,除直角外,共有五个元素,即三条边和两个锐角。
由直角三角形中的已知元素,求出其余未知元素的过程,叫作解直角三角形.新知探究(∠A、∠B、AB)已知两条直角边,可以解直角三角形习题精讲变式1 在Rt△ABC中,∠C = 90°, 分别是
的对边,已知 ,
解这个直角三角形.解:(∠A、∠B、b)已知一条直角边和一条斜边,可以解直角三角形习题精讲变式2 在Rt△ABC中,∠C = 90°, 分别是
的对边,已知 ,
解这个直角三角形.
解:方法一(∠B、b、c)习题精讲变式2 在Rt△ABC中,∠C = 90°, 分别是
的对边,已知 ,
解这个直角三角形.
解:方法二已知一锐角和它的对边,可以解直角三角形习题精讲变式3 在Rt△ABC中,∠C = 90°, 分别是
的对边,已知 ,
解这个直角三角形.解:方法一(∠A、b、c)习题精讲变式3 在Rt△ABC中,∠C = 90°, 分别是
的对边,已知 ,
解这个直角三角形.解:方法二习题精讲变式3 在Rt△ABC中,∠C = 90°, 分别是
的对边,已知 ,
解这个直角三角形.解:方法三已知一锐角和它的邻边,可以解直角三角形习题精讲变式4 在Rt△ABC中, , 分别是
的对边,已知 ,
解这个直角三角形.解:方法一方法二(∠A、a、b)已知一锐角和斜边,可以解直角三角形新知探究已知两角能否解直角三角形? 归纳总结解直角三角形必备条件已知两边解直角三角形已知一个锐角和一边解直角三角形只要知道五个元素中的两个元素 就可以求出余下的三个未知元素(至少有一个是边)针对训练 在Rt△ABC中,有下列情况,则直角三角形可解的是( )
A.已知
B.已知
C.已知
D.已知D生活中的数学设塔顶中心点为B,塔身中心线与垂直中心线的夹角为∠ A,过B点向垂直中心线引垂线,垂足为点C(如图),在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m.问:倾斜角∠A是多少?所以∠A≈5.48°ABC解:新知探究例2 如图,在Rt△ABC中,∠C=90°,∠B=35°,b=20,解这个直角三角形 (结果保留小数点后一位).跟踪训练 在 Rt△ABC 中,∠C=90°,∠B=72°,c = 14.
根据条件解直角三角形.
( 参考数据: )解:课堂小结解直角三角形依据只要知道五个元素中的两个元素(至少有一个是边),就可以求出余下的三个未知元素勾股定理两锐角互余锐角三角函数已知斜边求直边,正弦余弦很方便;
已知直边求直边,正切余切理当然;
已知两边求一角,函数关系要选好;
已知两边求一边,勾股定理最方便;
已知锐角求锐角,互余关系要记好;
已知直边求斜边,用除还需正余弦;
计算方法要选择,能用乘法不用除.优选关系式家庭作业1. 如图,在Rt△ABC中,∠C=90°,∠B=30°,
AB=8,则BC的长是 ( )2. 在Rt△ABC中,∠C=90°,∠B=37°,BC=32,则
AC = (参考数据:sin37°≈0.60,cos37°≈0.80,
tan37°≈0.75).家庭作业3. 在Rt△ABC 中, ,
,根据下列条件解直角三角形:
(1)
(2)
(3) 家庭作业【选做】 如图,在Rt△ABC 中,∠C=90°,cosA = ,
BC = 5, 试求AB的长.
