28.2.2 解直角三角形及其 应用举例仰角、俯角问题(第1课时 共24张PPT)
文档属性
| 名称 | 28.2.2 解直角三角形及其 应用举例仰角、俯角问题(第1课时 共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 00:00:00 | ||
图片预览








文档简介
课件24张PPT。
人教版 九年级数学下册
第28章 锐角三角函数
28.2.2 解直角三角形应用举例(第1课时)
仰角、俯角问题
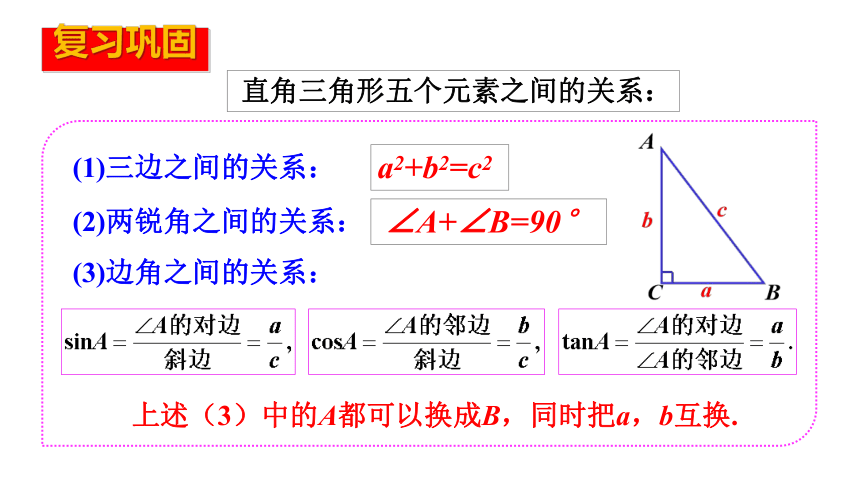
复习巩固(2)两锐角之间的关系:∠A+∠B=90°(3)边角之间的关系:(1)三边之间的关系: a2+b2=c2 上述(3)中的A都可以换成B,同时把a,b互换. 直角三角形五个元素之间的关系:情景引入“神州”九号载人航天飞船与“天宫”一号成功对接 “神州”九号与“天宫”一号的组合体在离地球表面343km的圆形轨道上运行,如图,当组合体运行到地球表面P点的正上方时,从中能看到的地球表面最远点在什么位置?最远点与P点的距离是多少(地球半径约为6400km,π取3.142,结果取整数)?情景引入1.知道仰角、俯角的概念.
2.会根据切线的性质及仰角、俯角的概念结合直角三角形的知识解决实际问题.重点:应用解直角三角形的知识解决实际问题.
难点:将实际问题抽象为数学问题.学习目标重点难点知识点一:利用圆的有关知识解直角三角形知识储备1.如图所示,PA切⊙O于点A,PO交⊙O于点B,⊙O的半径为1cm,PB=1cm,则∠AOB=_____,AB=______(1)圆的切线有什么性质?
(2)在△PAO中,怎样求锐角∠AOB的度数?
(3)弧长公式是什么??60°??切线的性质定理:圆的切线垂直于过切点的半径在直角三角形中,已知一锐角,可以求另一锐角度数;
已知任意两边,通过边与角的关系,利用锐角三角函数求出一锐角度数。知识点一:利用圆的有关知识解直角三角形典例讲评例3:2012年6月18日,“神舟”九号载人航天飞船与“天宫”一号目标 飞行器成功实现交会对接.“神舟”九号与“天宫”一号的组合体在离地球表 面343 km的圆形轨道上运行,如图,当组合体运行到地球表面P点的正上方时,从中能看到的地球表面最远点在什么位置?最远点与P点的距离是多少(地球半径约为6400km,π取3.142,结果取整数)?知识点一:利用圆的有关知识解直角三角形典例讲评分析:
组合体 地球看视线是切线最远点是切点?知识点一:利用圆的有关知识解直角三角形典例讲评解:设∠POQ =α,在图中,FQ是⊙O的切线,△FOQ是直角三角形.∴弧 PQ的长为 当飞船在P点正上方时,最远点距离P点约2051km?????学以致用1.如图是一个匀速旋转的摩天轮示意图,O为圆心,AB为水平地面,假设摩天轮的直径为80m,最低点C离地面6m,旋转一周所用的时间为6min,小明从点C乘坐摩天轮(身高忽略不计),请问:经过2min后,小明离
地面的高度是多少米?知识点一:利用圆的有关知识解直角三角形?∴OG=OE·cos∠GOE=20(m)∴小明离地面的高度是:OG+OC+CD=20+40+6=66(m).归纳总结利用解直角三角形解决实物模型问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形问题);
(2)根据问题中的条件,适当选用锐角三角函数等解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案。新知探究知识点二:利用仰角、俯角解直角三角形 平时我们观察物体时,我们的视线相对于水平线来说可有几种情况?三种:
重叠、向上和向下新知归纳知识点二:利用仰角、俯角解直角三角形 如图,在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.仰角﹙俯角﹙典例讲评例4:热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120 m,这栋楼有多高(结果取整数)?知识点二:利用仰角、俯角解直角三角形仰角俯角典例讲评知识点二:利用仰角、俯角解直角三角形?答:这栋楼高约为277 m.∴BC=BD+CD=??????学以致用知识点二:利用仰角、俯角解直角三角形?C学以致用知识点二:利用仰角、俯角解直角三角形?D学以致用知识点二:利用仰角、俯角解直角三角形3.如图,在高度为10米的平台CD上测得一高层建筑物AB的顶端A的仰角为60°,底端B的俯角为30°,则高层建筑物的高AB= 米.40归纳总结?解含有仰角、俯角问题的方法
(1)仰角和俯角是指视线相对于水平线而言的,不同位置的仰角和俯角是不同的,可巧记为“上仰下俯”;
(2)视线、水平线、物体的高构成直角三角形,已知仰角(俯角)和另一边,利用解直角三角形的知识就可以求出物体的高度;
(3)弄清仰角、俯角的定义,根据题意画出几何图形,将实际问题中的数量关系归结到直角三角形中来求解.课后练习知识点二:利用仰角、俯角解直角三角形?解:课堂小结 1. 学习了仰角、俯角的概念。如图,在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.
仰角﹙俯角﹙2.会根据切线的性质及仰角、俯角的概念结合直角三角形的知识解决实际问题.课堂小结利用解直角三角形解决实物模型问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形问题);
(2)根据问题中的条件,适当选用锐角三角函数等解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案。1.如图,某高速公路建设中需要确定隧道AB的长度.已知在离地面1500m高度C处的飞机上,测量人员测得正前方A、B两点处的俯角分别为60°和45° 求隧道AB的长( ≈1.73).课后作业?2. 为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置个平面镜E,使得B,E,D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED).在F处测得旗杆
顶A的仰角为39.3°,平面镜E的俯角
为45°,FD=1.8米,问旗杆AB的高度约
为多少米? (结果保留整数)(参考数据:tan39.3°≈0.82,tan84.3°≈10.02)课后作业
人教版 九年级数学下册
第28章 锐角三角函数
28.2.2 解直角三角形应用举例(第1课时)
仰角、俯角问题
复习巩固(2)两锐角之间的关系:∠A+∠B=90°(3)边角之间的关系:(1)三边之间的关系: a2+b2=c2 上述(3)中的A都可以换成B,同时把a,b互换. 直角三角形五个元素之间的关系:情景引入“神州”九号载人航天飞船与“天宫”一号成功对接 “神州”九号与“天宫”一号的组合体在离地球表面343km的圆形轨道上运行,如图,当组合体运行到地球表面P点的正上方时,从中能看到的地球表面最远点在什么位置?最远点与P点的距离是多少(地球半径约为6400km,π取3.142,结果取整数)?情景引入1.知道仰角、俯角的概念.
2.会根据切线的性质及仰角、俯角的概念结合直角三角形的知识解决实际问题.重点:应用解直角三角形的知识解决实际问题.
难点:将实际问题抽象为数学问题.学习目标重点难点知识点一:利用圆的有关知识解直角三角形知识储备1.如图所示,PA切⊙O于点A,PO交⊙O于点B,⊙O的半径为1cm,PB=1cm,则∠AOB=_____,AB=______(1)圆的切线有什么性质?
(2)在△PAO中,怎样求锐角∠AOB的度数?
(3)弧长公式是什么??60°??切线的性质定理:圆的切线垂直于过切点的半径在直角三角形中,已知一锐角,可以求另一锐角度数;
已知任意两边,通过边与角的关系,利用锐角三角函数求出一锐角度数。知识点一:利用圆的有关知识解直角三角形典例讲评例3:2012年6月18日,“神舟”九号载人航天飞船与“天宫”一号目标 飞行器成功实现交会对接.“神舟”九号与“天宫”一号的组合体在离地球表 面343 km的圆形轨道上运行,如图,当组合体运行到地球表面P点的正上方时,从中能看到的地球表面最远点在什么位置?最远点与P点的距离是多少(地球半径约为6400km,π取3.142,结果取整数)?知识点一:利用圆的有关知识解直角三角形典例讲评分析:
组合体 地球看视线是切线最远点是切点?知识点一:利用圆的有关知识解直角三角形典例讲评解:设∠POQ =α,在图中,FQ是⊙O的切线,△FOQ是直角三角形.∴弧 PQ的长为 当飞船在P点正上方时,最远点距离P点约2051km?????学以致用1.如图是一个匀速旋转的摩天轮示意图,O为圆心,AB为水平地面,假设摩天轮的直径为80m,最低点C离地面6m,旋转一周所用的时间为6min,小明从点C乘坐摩天轮(身高忽略不计),请问:经过2min后,小明离
地面的高度是多少米?知识点一:利用圆的有关知识解直角三角形?∴OG=OE·cos∠GOE=20(m)∴小明离地面的高度是:OG+OC+CD=20+40+6=66(m).归纳总结利用解直角三角形解决实物模型问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形问题);
(2)根据问题中的条件,适当选用锐角三角函数等解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案。新知探究知识点二:利用仰角、俯角解直角三角形 平时我们观察物体时,我们的视线相对于水平线来说可有几种情况?三种:
重叠、向上和向下新知归纳知识点二:利用仰角、俯角解直角三角形 如图,在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.仰角﹙俯角﹙典例讲评例4:热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120 m,这栋楼有多高(结果取整数)?知识点二:利用仰角、俯角解直角三角形仰角俯角典例讲评知识点二:利用仰角、俯角解直角三角形?答:这栋楼高约为277 m.∴BC=BD+CD=??????学以致用知识点二:利用仰角、俯角解直角三角形?C学以致用知识点二:利用仰角、俯角解直角三角形?D学以致用知识点二:利用仰角、俯角解直角三角形3.如图,在高度为10米的平台CD上测得一高层建筑物AB的顶端A的仰角为60°,底端B的俯角为30°,则高层建筑物的高AB= 米.40归纳总结?解含有仰角、俯角问题的方法
(1)仰角和俯角是指视线相对于水平线而言的,不同位置的仰角和俯角是不同的,可巧记为“上仰下俯”;
(2)视线、水平线、物体的高构成直角三角形,已知仰角(俯角)和另一边,利用解直角三角形的知识就可以求出物体的高度;
(3)弄清仰角、俯角的定义,根据题意画出几何图形,将实际问题中的数量关系归结到直角三角形中来求解.课后练习知识点二:利用仰角、俯角解直角三角形?解:课堂小结 1. 学习了仰角、俯角的概念。如图,在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.
仰角﹙俯角﹙2.会根据切线的性质及仰角、俯角的概念结合直角三角形的知识解决实际问题.课堂小结利用解直角三角形解决实物模型问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形问题);
(2)根据问题中的条件,适当选用锐角三角函数等解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案。1.如图,某高速公路建设中需要确定隧道AB的长度.已知在离地面1500m高度C处的飞机上,测量人员测得正前方A、B两点处的俯角分别为60°和45° 求隧道AB的长( ≈1.73).课后作业?2. 为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置个平面镜E,使得B,E,D在同一水平线上,如图所示.该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED).在F处测得旗杆
顶A的仰角为39.3°,平面镜E的俯角
为45°,FD=1.8米,问旗杆AB的高度约
为多少米? (结果保留整数)(参考数据:tan39.3°≈0.82,tan84.3°≈10.02)课后作业
