28.2.2 解直角三角形应用举例坡度、坡角问题(第2课时 共21张PPT)
文档属性
| 名称 | 28.2.2 解直角三角形应用举例坡度、坡角问题(第2课时 共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 703.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 00:00:00 | ||
图片预览




文档简介
课件21张PPT。
人教版 九年级数学下册
第28章 锐角三角函数
28.2.2 解直角三角形应用举例(第2课时)
坡度、坡角问题问题
情景引入水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1:3,斜坡CD的坡度i' =1:2.5,求斜坡AB的坡角? ,坝底宽AD和斜坡AB的长.1.知道坡度、坡角的概念
2.解关于坡度坡角的实际应用问题.重点:用解直角三角形的知识解决与坡度、坡角有关的实际问题.
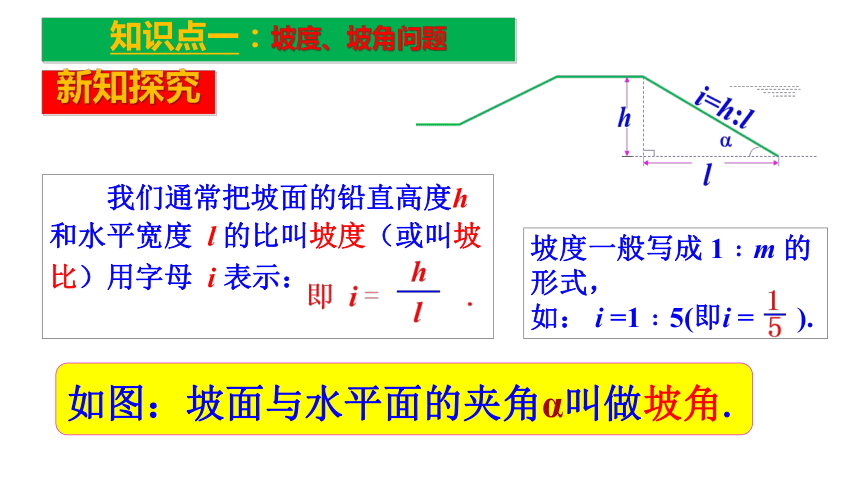
难点:将实际问题抽象为数学问题.学习目标重点难点知识点一:坡度、坡角问题新知探究 我们通常把坡面的铅直高度h和水平宽度 l 的比叫坡度(或叫坡比)用字母 i 表示:
如图:坡面与水平面的夹角α叫做坡角.坡度一般写成 1﹕m 的形式,
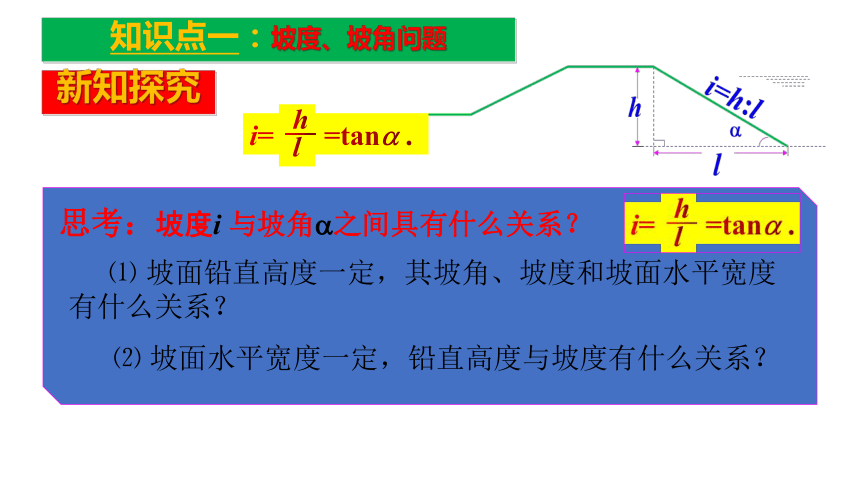
如: i =1﹕5(即i = ).知识点一:坡度、坡角问题新知探究思考:坡度i 与坡角?之间具有什么关系?
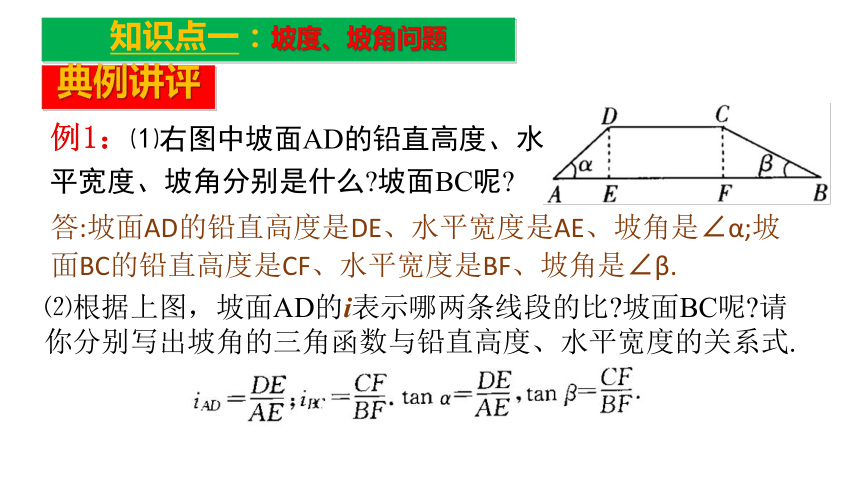
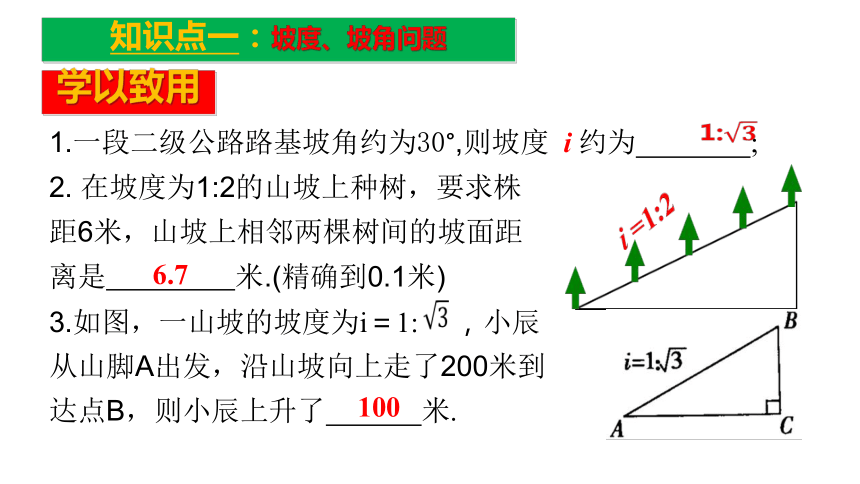
⑴ 坡面铅直高度一定,其坡角、坡度和坡面水平宽度有什么关系?⑵ 坡面水平宽度一定,铅直高度与坡度有什么关系?典例讲评例1:⑴右图中坡面AD的铅直高度、水平宽度、坡角分别是什么?坡面BC呢?知识点一:坡度、坡角问题⑵根据上图,坡面AD的i表示哪两条线段的比?坡面BC呢?请你分别写出坡角的三角函数与铅直高度、水平宽度的关系式.答:坡面AD的铅直高度是DE、水平宽度是AE、坡角是∠α;坡面BC的铅直高度是CF、水平宽度是BF、坡角是∠β.学以致用1.一段二级公路路基坡角约为30°,则坡度 i 约为 ;
2. 在坡度为1:2的山坡上种树,要求株
距6米,山坡上相邻两棵树间的坡面距
离是 米.(精确到0.1米)
3.如图,一山坡的坡度为i=1: ,小辰
从山脚A出发,沿山坡向上走了200米到
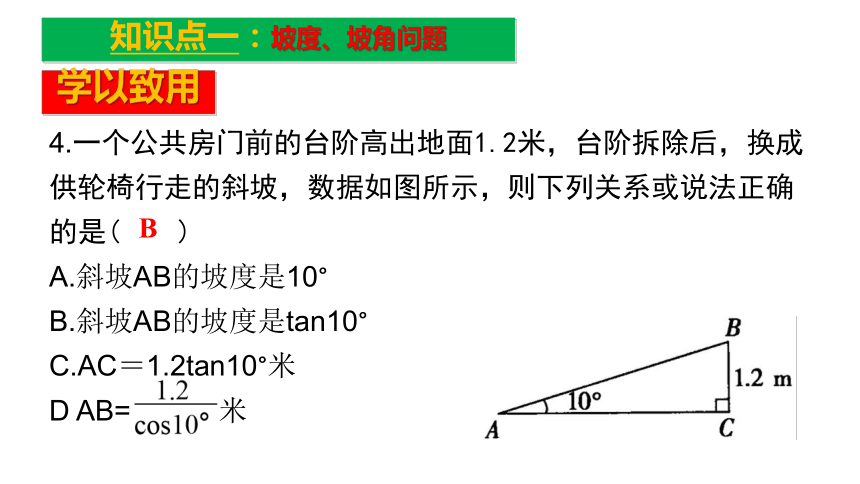
达点B,则小辰上升了 米.知识点一:坡度、坡角问题?6.7100?学以致用4.一个公共房门前的台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说法正确的是( )
A.斜坡AB的坡度是10°
B.斜坡AB的坡度是tan10°
C.AC=1.2tan10°米
D AB= 米知识点一:坡度、坡角问题B新知归纳注意:
⑴坡度的结果不是一个度数,而是一个比值,不要与坡角相混淆;
⑵坡度通常写成“ h:l ”的形式
⑶坡度i 和坡角α的关系为i=tanα.知识点一:坡度、坡角问题典例讲评例2:水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1:3,斜坡CD的坡度i' =1:2.5,求坝底宽AD和斜坡AB的长.
(精确到0.1m,tan18°26′ ≈0.3333,sin18°26′≈0.3162)知识点二:坡度、坡角的实际应用典例讲评知识点二:坡度、坡角的实际应用解:作BE⊥AD,CF⊥AD.∴ AE=3BE=3×23=69(m) ,
FD=2.5CF=2.5×23=57.5(m).∴AD=AE+EF+FD=69+6+57.5
=132.5(m) .在Rt△ABE和Rt△CDF中,因为斜坡AB的坡度 ≈ 72.7(m) . 答:AD的宽度为132.5m,
AB的长为72.7m.学以致用知识点二:坡度、坡角的实际应用??归纳总结知识点二:坡度、坡角的实际应用 解决坡度问题时,可适当添加辅助线,将梯形分割为直角三角形和矩形来解决问题.学以致用1.如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了____米.(参考数据:sin 34°≈0.56,cos 34°≈0.83,tan 34°≈0.67)280知识点二:坡度、坡角的实际应用学以致用2.如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1∶0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin 40°≈0.64,
cos 40°≈0.77,tan 40°≈0.84)
A.5.1米 B.6.3米
C.7.1米 D.9.2米知识点二:坡度、坡角的实际应用A?学以致用知识点二:坡度、坡角的实际应用8归纳总结知识点二:坡度、坡角的实际应用利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.课堂小结1.坡度:我们通常把坡面的铅直高度h和水平宽度 l 的比叫坡度(或叫坡比)用字母 i 表示:
2.坡角:坡面与水平面的夹角α叫做坡角
注意:
⑴坡度的结果不是一个度数,而是一个比值,不要与坡角相混淆;
⑵坡度通常写成“ h:l ”的形式
⑶坡度i 和坡角α的关系为i=tanα.课堂小结 在解决坡度的实际问题时,可适当添加辅助线,将梯形分割为直角三角形和矩形来解决问题.?课后作业2.如图,河的两岸l1与l2相互平行,A,B是l1上的两点,C,D是l2上的两点.某人在点A处测得∠CAB=90°,
∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C,D两点间的距离.
课后作业
人教版 九年级数学下册
第28章 锐角三角函数
28.2.2 解直角三角形应用举例(第2课时)
坡度、坡角问题问题
情景引入水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1:3,斜坡CD的坡度i' =1:2.5,求斜坡AB的坡角? ,坝底宽AD和斜坡AB的长.1.知道坡度、坡角的概念
2.解关于坡度坡角的实际应用问题.重点:用解直角三角形的知识解决与坡度、坡角有关的实际问题.
难点:将实际问题抽象为数学问题.学习目标重点难点知识点一:坡度、坡角问题新知探究 我们通常把坡面的铅直高度h和水平宽度 l 的比叫坡度(或叫坡比)用字母 i 表示:
如图:坡面与水平面的夹角α叫做坡角.坡度一般写成 1﹕m 的形式,
如: i =1﹕5(即i = ).知识点一:坡度、坡角问题新知探究思考:坡度i 与坡角?之间具有什么关系?
⑴ 坡面铅直高度一定,其坡角、坡度和坡面水平宽度有什么关系?⑵ 坡面水平宽度一定,铅直高度与坡度有什么关系?典例讲评例1:⑴右图中坡面AD的铅直高度、水平宽度、坡角分别是什么?坡面BC呢?知识点一:坡度、坡角问题⑵根据上图,坡面AD的i表示哪两条线段的比?坡面BC呢?请你分别写出坡角的三角函数与铅直高度、水平宽度的关系式.答:坡面AD的铅直高度是DE、水平宽度是AE、坡角是∠α;坡面BC的铅直高度是CF、水平宽度是BF、坡角是∠β.学以致用1.一段二级公路路基坡角约为30°,则坡度 i 约为 ;
2. 在坡度为1:2的山坡上种树,要求株
距6米,山坡上相邻两棵树间的坡面距
离是 米.(精确到0.1米)
3.如图,一山坡的坡度为i=1: ,小辰
从山脚A出发,沿山坡向上走了200米到
达点B,则小辰上升了 米.知识点一:坡度、坡角问题?6.7100?学以致用4.一个公共房门前的台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或说法正确的是( )
A.斜坡AB的坡度是10°
B.斜坡AB的坡度是tan10°
C.AC=1.2tan10°米
D AB= 米知识点一:坡度、坡角问题B新知归纳注意:
⑴坡度的结果不是一个度数,而是一个比值,不要与坡角相混淆;
⑵坡度通常写成“ h:l ”的形式
⑶坡度i 和坡角α的关系为i=tanα.知识点一:坡度、坡角问题典例讲评例2:水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1:3,斜坡CD的坡度i' =1:2.5,求坝底宽AD和斜坡AB的长.
(精确到0.1m,tan18°26′ ≈0.3333,sin18°26′≈0.3162)知识点二:坡度、坡角的实际应用典例讲评知识点二:坡度、坡角的实际应用解:作BE⊥AD,CF⊥AD.∴ AE=3BE=3×23=69(m) ,
FD=2.5CF=2.5×23=57.5(m).∴AD=AE+EF+FD=69+6+57.5
=132.5(m) .在Rt△ABE和Rt△CDF中,因为斜坡AB的坡度 ≈ 72.7(m) . 答:AD的宽度为132.5m,
AB的长为72.7m.学以致用知识点二:坡度、坡角的实际应用??归纳总结知识点二:坡度、坡角的实际应用 解决坡度问题时,可适当添加辅助线,将梯形分割为直角三角形和矩形来解决问题.学以致用1.如图,一名滑雪运动员沿着倾斜角为34°的斜坡,从A滑行至B,已知AB=500米,则这名滑雪运动员的高度下降了____米.(参考数据:sin 34°≈0.56,cos 34°≈0.83,tan 34°≈0.67)280知识点二:坡度、坡角的实际应用学以致用2.如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1∶0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin 40°≈0.64,
cos 40°≈0.77,tan 40°≈0.84)
A.5.1米 B.6.3米
C.7.1米 D.9.2米知识点二:坡度、坡角的实际应用A?学以致用知识点二:坡度、坡角的实际应用8归纳总结知识点二:坡度、坡角的实际应用利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.课堂小结1.坡度:我们通常把坡面的铅直高度h和水平宽度 l 的比叫坡度(或叫坡比)用字母 i 表示:
2.坡角:坡面与水平面的夹角α叫做坡角
注意:
⑴坡度的结果不是一个度数,而是一个比值,不要与坡角相混淆;
⑵坡度通常写成“ h:l ”的形式
⑶坡度i 和坡角α的关系为i=tanα.课堂小结 在解决坡度的实际问题时,可适当添加辅助线,将梯形分割为直角三角形和矩形来解决问题.?课后作业2.如图,河的两岸l1与l2相互平行,A,B是l1上的两点,C,D是l2上的两点.某人在点A处测得∠CAB=90°,
∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C,D两点间的距离.
课后作业
