人教版数学八年级下册:18.1.1 平行四边形的性质(第1课时 共30张PPT)
文档属性
| 名称 | 人教版数学八年级下册:18.1.1 平行四边形的性质(第1课时 共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-16 23:29:03 | ||
图片预览





文档简介
课件30张PPT。
人教版 八年级数学下册
第18章 平行四边形
18.1.1 平行四边形的性质(第1课时)
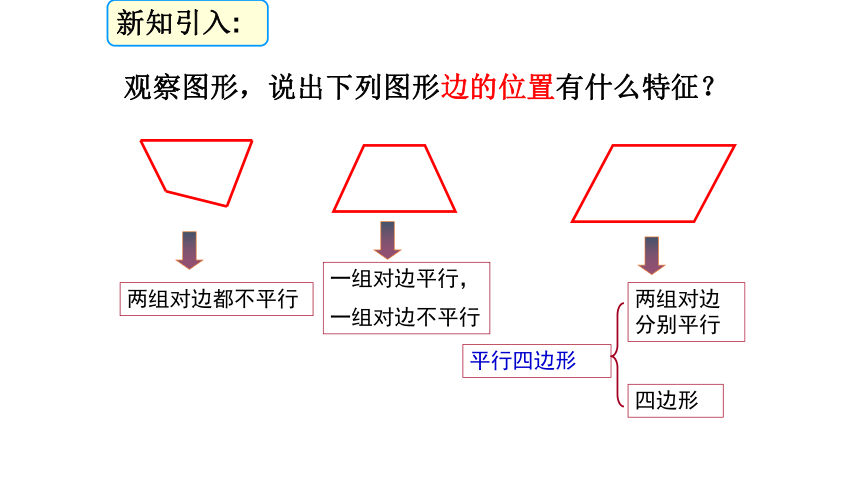
寻找生活中的平行四边形两组对边都不平行一组对边平行,
一组对边不平行两组对边分别平行四边形平行四边形观察图形,说出下列图形边的位置有什么特征?新知引入:两组对边分别平行的四边形叫做平行四边形DCAB注意:平行四边形的各顶点字母按顺时针或逆时针
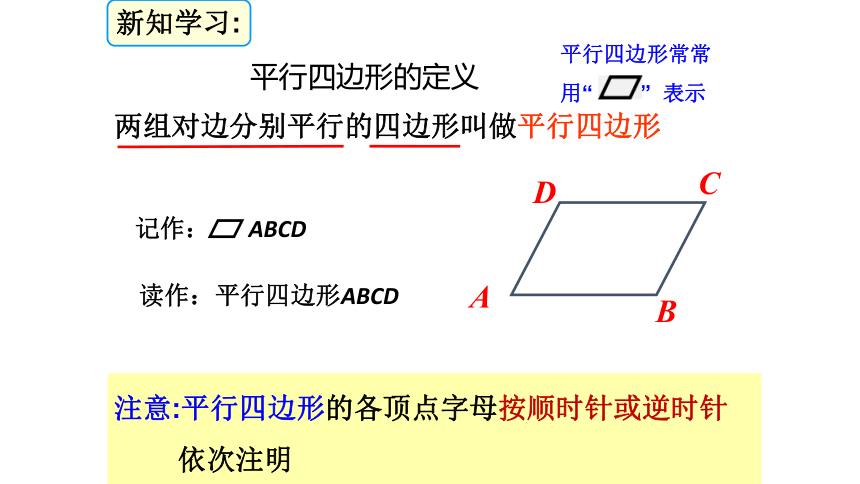
依次注明新知学习:平行四边形的定义平行四边形常常
用“ ” 表示记作: ABCD读作:平行四边形ABCD
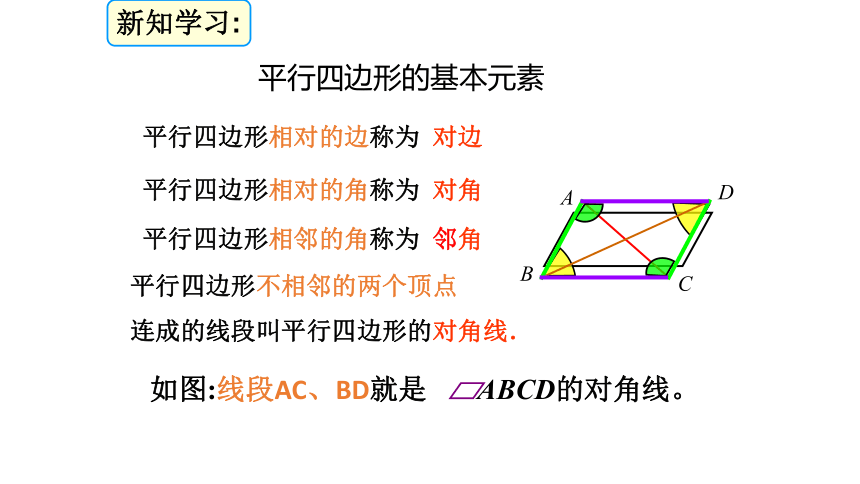
平行四边形相对的边称为 对边
新知学习:平行四边形的基本元素平行四边形相对的角称为 对角
平行四边形相邻的角称为 邻角
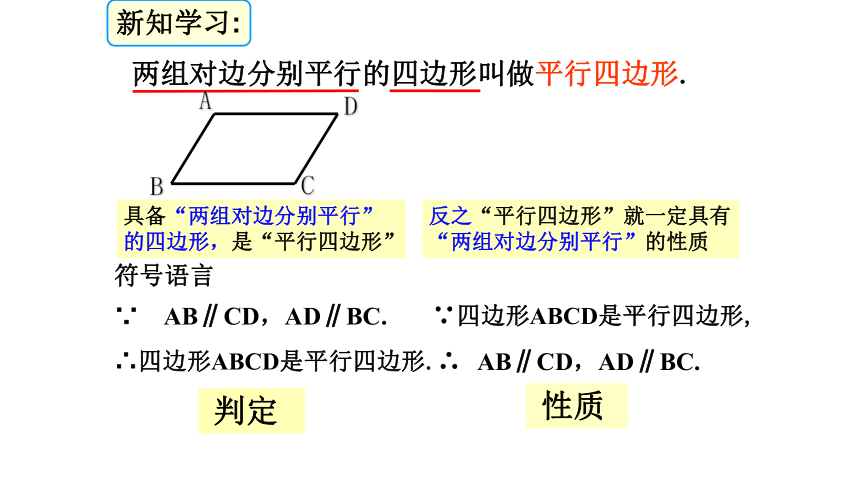
两组对边分别平行的四边形叫做平行四边形.∴四边形ABCD是平行四边形.∵四边形ABCD是平行四边形,具备“两组对边分别平行”
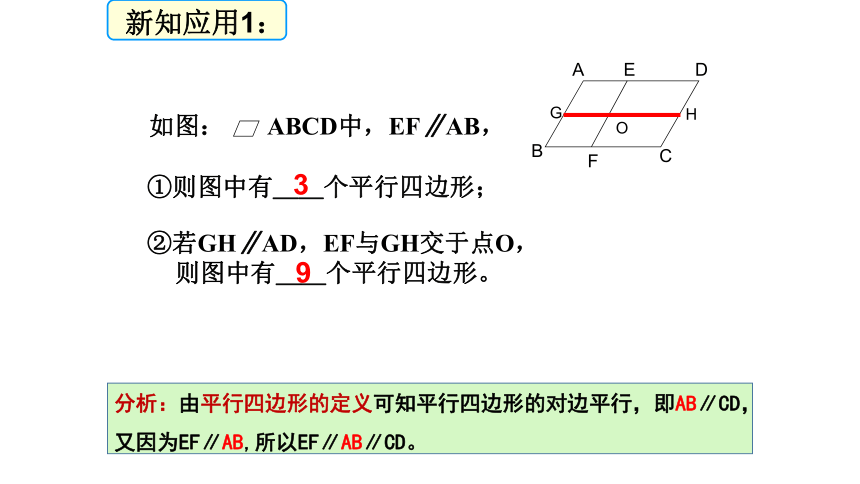
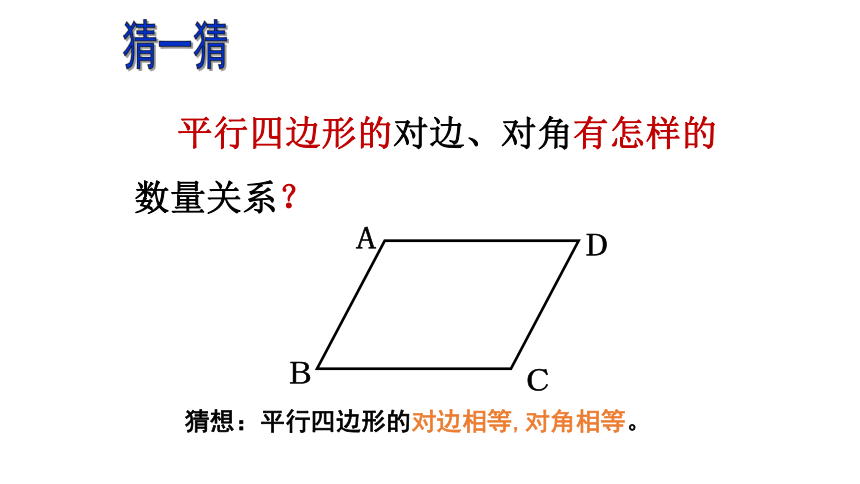
的四边形,是“平行四边形”反之“平行四边形”就一定具有“两组对边分别平行”的性质符号语言 判定 性质新知学习:①则图中有__个平行四边形;39 新知应用1:分析:由平行四边形的定义可知平行四边形的对边平行,即AB∥CD,又因为EF∥AB,所以EF∥AB∥CD。 根据定义画出一个平行四边形。画一画 平行四边形的对边、对角有怎样的数量关系?猜一猜猜想:平行四边形的对边相等,对角相等。ABCD 请用尺子等工具度量你手中平行四边形的四条边,并记录下数据,你能发现AB与DC,AD与BC之间的数量关系吗?测得AB=DC,AD=BC.新知探究1AB=8.4cmDC=8.4cmAD=4.3cmBC=4.3cm平行四边形的对边相等.ABCD测得∠A =∠C,∠B =∠D. 请用量角器等工具度量你手中平行四边形的四个角,并记录下数据,你能发现∠A与∠C,∠B与 ∠D之间的数量关系吗?怎样用以前所学的知识和方法证明这两个猜想呢?新知探究1∠A=60°∠B=120°∠c=60°∠D=120°平行四边形的对角相等.已知:如图,在 ABCD中,
求证:AB=CD,BC=DA,
∠A=∠C,∠B=∠D.
分析:我们先来看边验证猜想:?利用三角形全等要证明: AB=CD,BC=DA,
到目前为止,我们有哪些方法可以证明两条线段相等??等角对等边图中没有现成的三角形,该怎么办?添加辅助线构造三角形平行四边形的对边相等,对角相等。证明: 已知:如图,在 ABCD中
求证:AB=CD,BC=DA,
∠BAD=∠DCB,∠B=∠D.
证明:连接验证猜想:新知归纳: ∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD.∴∠1=∠2,∠3=∠4.在△ABC和△CDA中∠1=∠2
AC=CA
∠3=∠4∴ △ABC≌△CDA.(ASA)∴AB=CD,BC=DA,
∠B=∠D,又∵∠1=∠2,∠3=∠4.∴∠1+∠3=∠2+∠4.即∠BAD=∠DCB.AC.证明:平行四边形的对边相等,对角相等。性质:平行四边形的对边相等。 ABCD平行四边形的性质新知归纳2:∵ 四边形ABCD是平行四边形, ∴ AB=CD,AD=BC,AB∥CD,AD∥BC. ∠ A=∠C ,∠B=∠D. 思考:平行四边形的邻角有什么关系呢?平行四边形的邻角互补。 相等且平行。性质1性质2 平行四边形的对角可证明线段平行或相等、
角相等。符号语言:四边形问题三角形问题转化连接对角线 思考 : 不添加辅助线,你能否直接运用平行四边形
的定义,证明其对角相等?小结归纳构造两个全等的三角形例1 如图,在 ABCD中。
∵四边形ABCD是平行四边形,∠A =32。解: ∴ ∠C = ∠A=32。, ∠B= ∠D. (平行四边形的对角相等). 又∵AD∥BC , (平行四边形的对边平行),∴ ∠A + ∠B =180。(两直线平行,同旁内角互补),∴ ∠B= ∠D= 180。- ∠A = 180。- 32。=148。例题讲解:变式:若∠A:∠B=2:3,求各角的度数。(1)若∠A =32。,求其余三个角的度数。32° 例1 如图,在 ABCD中,
若∠A:∠B=2:3,求各角的度数。
例题讲解:∵四边形ABCD是平行四边形,
∴AD∥ BC .
∴∠A+∠B=180°.∴2x+3x= 180°,
∴ x= 36°. 解:设∠A=2x°,∴ ∠A = ∠C=72°, ∠B= ∠D=108°则∠B=3x° 已知平行四边形的边角的比例关系求其他边角时,常会用到方程思想,结合平行四边形的性质列方程.(2)连接AC,已知 ABCD的周长等于28 cm,AC=7cm,求△ABC的周长。
例题讲解:解: (2) ∵四边形ABCD是平行四边形
∴AB=CD,BC=AD.
又∵AB+BC+CD+AD=28cm,
∴AB+BC=14cm,
∵AC=7cm,
∴△ABC的周长为AB+BC+AC= 21cm。 分析:平行四边形ABCD 的周长 =AB+BC+CD+DA,根据平行四边形的对边相等,平行四边形的两条邻边之和等于平行四边形周长的一半。平行四边形ABCD 的 周长 =2(AB+BC)。 如图,在1.若∠A=130°,则∠B=______ ,∠C=______,∠D=______。A:基础知识:B:变式训练:2.若∠A+ ∠C= 200°,则∠A=______ ,∠B=______。50°130°50°100°80° 新知应用2:C:拓展延伸:120°60°数形结合60°?? 如图在A基础知识:1.若AB=1㎝,BC=2 ㎝。B变式训练:2.若AB:BC=3:4,周长为14㎝,则CD= ,DA=______。
3.若AB=x-4,BC=x+3,CD=6㎝,则AD=______6cm 3cm4cm13cm。 新知应用2:x-4x+36如图,在 ABCD中,∠ABC的平分线BE交AD于E,BC=5,
AB=3,则ED的长为 .
2 16或14C拓展延伸: 新知应用2:3532322数形结合,
分类讨论。213证明: ∵四边形ABCD是平行四边形,
∴ ∠A= ∠C,AD=CB.
又∠AED= ∠CFB=90°,
∴ △ADE≌△CBF(AAS).
∴AE=CF. DE和BF相等吗?例题讲解:DE=BF
分析:要证AE=CF,可证ADE≌△CBF。由平行四边形的对角相等,对边相等,和垂直条件证全等。
A B C D E F abAD与BC对边相等N1 M1 Q1 P1 N2M2 Q2 P2M1N1//P1Q1
M2N2//P2Q2
AD//BC
M1N1=P1Q1M2N2=P2Q2若a // b,作 M1N1//P1Q1,分别交a于M1,P1,交 b 于N1,Q1。则线段 M1N1与P1Q1有什么关系?新知探究2 结论 :两条平行线之间的任何两条 ________
都相等。平行线段 新知归纳2:abN2M2Q2 P2 A B 直线a上所有点到直线b上的距离都相等。新知探究2点到直线的距离可得M2N2=P2Q2=AB结论: 两条平行线中,______________________
————————————————————,叫做这两条
平行线之间的距离。 一条直线上的任意一点到另一条直线的距离 两条平行线间的距离相等。新知归纳2:若a//b,点A是直线a上任意一点,且AB⊥b,B是垂足,线段AB的长就是直线a,b之间的距离。BDDCABDC 新知应用3:18.1.1 平行四边形的性质课堂小结分类讨论思想数形结合思想选做 1.数学书第43页练习第1,2题;
2.不添加辅助线,直接运用平行四边形的定义, 证明其对角相等。
作业必做 △ABC是等腰三角形,AB=AC, P是底边BC
上一动点,PE∥AB,PF∥AC,点E,F分别在AC,AB
上.求证:PE+PF=AB.
人教版 八年级数学下册
第18章 平行四边形
18.1.1 平行四边形的性质(第1课时)
寻找生活中的平行四边形两组对边都不平行一组对边平行,
一组对边不平行两组对边分别平行四边形平行四边形观察图形,说出下列图形边的位置有什么特征?新知引入:两组对边分别平行的四边形叫做平行四边形DCAB注意:平行四边形的各顶点字母按顺时针或逆时针
依次注明新知学习:平行四边形的定义平行四边形常常
用“ ” 表示记作: ABCD读作:平行四边形ABCD
平行四边形相对的边称为 对边
新知学习:平行四边形的基本元素平行四边形相对的角称为 对角
平行四边形相邻的角称为 邻角
两组对边分别平行的四边形叫做平行四边形.∴四边形ABCD是平行四边形.∵四边形ABCD是平行四边形,具备“两组对边分别平行”
的四边形,是“平行四边形”反之“平行四边形”就一定具有“两组对边分别平行”的性质符号语言 判定 性质新知学习:①则图中有__个平行四边形;39 新知应用1:分析:由平行四边形的定义可知平行四边形的对边平行,即AB∥CD,又因为EF∥AB,所以EF∥AB∥CD。 根据定义画出一个平行四边形。画一画 平行四边形的对边、对角有怎样的数量关系?猜一猜猜想:平行四边形的对边相等,对角相等。ABCD 请用尺子等工具度量你手中平行四边形的四条边,并记录下数据,你能发现AB与DC,AD与BC之间的数量关系吗?测得AB=DC,AD=BC.新知探究1AB=8.4cmDC=8.4cmAD=4.3cmBC=4.3cm平行四边形的对边相等.ABCD测得∠A =∠C,∠B =∠D. 请用量角器等工具度量你手中平行四边形的四个角,并记录下数据,你能发现∠A与∠C,∠B与 ∠D之间的数量关系吗?怎样用以前所学的知识和方法证明这两个猜想呢?新知探究1∠A=60°∠B=120°∠c=60°∠D=120°平行四边形的对角相等.已知:如图,在 ABCD中,
求证:AB=CD,BC=DA,
∠A=∠C,∠B=∠D.
分析:我们先来看边验证猜想:?利用三角形全等要证明: AB=CD,BC=DA,
到目前为止,我们有哪些方法可以证明两条线段相等??等角对等边图中没有现成的三角形,该怎么办?添加辅助线构造三角形平行四边形的对边相等,对角相等。证明: 已知:如图,在 ABCD中
求证:AB=CD,BC=DA,
∠BAD=∠DCB,∠B=∠D.
证明:连接验证猜想:新知归纳: ∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD.∴∠1=∠2,∠3=∠4.在△ABC和△CDA中∠1=∠2
AC=CA
∠3=∠4∴ △ABC≌△CDA.(ASA)∴AB=CD,BC=DA,
∠B=∠D,又∵∠1=∠2,∠3=∠4.∴∠1+∠3=∠2+∠4.即∠BAD=∠DCB.AC.证明:平行四边形的对边相等,对角相等。性质:平行四边形的对边相等。 ABCD平行四边形的性质新知归纳2:∵ 四边形ABCD是平行四边形, ∴ AB=CD,AD=BC,AB∥CD,AD∥BC. ∠ A=∠C ,∠B=∠D. 思考:平行四边形的邻角有什么关系呢?平行四边形的邻角互补。 相等且平行。性质1性质2 平行四边形的对角可证明线段平行或相等、
角相等。符号语言:四边形问题三角形问题转化连接对角线 思考 : 不添加辅助线,你能否直接运用平行四边形
的定义,证明其对角相等?小结归纳构造两个全等的三角形例1 如图,在 ABCD中。
∵四边形ABCD是平行四边形,∠A =32。解: ∴ ∠C = ∠A=32。, ∠B= ∠D. (平行四边形的对角相等). 又∵AD∥BC , (平行四边形的对边平行),∴ ∠A + ∠B =180。(两直线平行,同旁内角互补),∴ ∠B= ∠D= 180。- ∠A = 180。- 32。=148。例题讲解:变式:若∠A:∠B=2:3,求各角的度数。(1)若∠A =32。,求其余三个角的度数。32° 例1 如图,在 ABCD中,
若∠A:∠B=2:3,求各角的度数。
例题讲解:∵四边形ABCD是平行四边形,
∴AD∥ BC .
∴∠A+∠B=180°.∴2x+3x= 180°,
∴ x= 36°. 解:设∠A=2x°,∴ ∠A = ∠C=72°, ∠B= ∠D=108°则∠B=3x° 已知平行四边形的边角的比例关系求其他边角时,常会用到方程思想,结合平行四边形的性质列方程.(2)连接AC,已知 ABCD的周长等于28 cm,AC=7cm,求△ABC的周长。
例题讲解:解: (2) ∵四边形ABCD是平行四边形
∴AB=CD,BC=AD.
又∵AB+BC+CD+AD=28cm,
∴AB+BC=14cm,
∵AC=7cm,
∴△ABC的周长为AB+BC+AC= 21cm。 分析:平行四边形ABCD 的周长 =AB+BC+CD+DA,根据平行四边形的对边相等,平行四边形的两条邻边之和等于平行四边形周长的一半。平行四边形ABCD 的 周长 =2(AB+BC)。 如图,在1.若∠A=130°,则∠B=______ ,∠C=______,∠D=______。A:基础知识:B:变式训练:2.若∠A+ ∠C= 200°,则∠A=______ ,∠B=______。50°130°50°100°80° 新知应用2:C:拓展延伸:120°60°数形结合60°?? 如图在A基础知识:1.若AB=1㎝,BC=2 ㎝。B变式训练:2.若AB:BC=3:4,周长为14㎝,则CD= ,DA=______。
3.若AB=x-4,BC=x+3,CD=6㎝,则AD=______6cm 3cm4cm13cm。 新知应用2:x-4x+36如图,在 ABCD中,∠ABC的平分线BE交AD于E,BC=5,
AB=3,则ED的长为 .
2 16或14C拓展延伸: 新知应用2:3532322数形结合,
分类讨论。213证明: ∵四边形ABCD是平行四边形,
∴ ∠A= ∠C,AD=CB.
又∠AED= ∠CFB=90°,
∴ △ADE≌△CBF(AAS).
∴AE=CF. DE和BF相等吗?例题讲解:DE=BF
分析:要证AE=CF,可证ADE≌△CBF。由平行四边形的对角相等,对边相等,和垂直条件证全等。
A B C D E F abAD与BC对边相等N1 M1 Q1 P1 N2M2 Q2 P2M1N1//P1Q1
M2N2//P2Q2
AD//BC
M1N1=P1Q1M2N2=P2Q2若a // b,作 M1N1//P1Q1,分别交a于M1,P1,交 b 于N1,Q1。则线段 M1N1与P1Q1有什么关系?新知探究2 结论 :两条平行线之间的任何两条 ________
都相等。平行线段 新知归纳2:abN2M2Q2 P2 A B 直线a上所有点到直线b上的距离都相等。新知探究2点到直线的距离可得M2N2=P2Q2=AB结论: 两条平行线中,______________________
————————————————————,叫做这两条
平行线之间的距离。 一条直线上的任意一点到另一条直线的距离 两条平行线间的距离相等。新知归纳2:若a//b,点A是直线a上任意一点,且AB⊥b,B是垂足,线段AB的长就是直线a,b之间的距离。BDDCABDC 新知应用3:18.1.1 平行四边形的性质课堂小结分类讨论思想数形结合思想选做 1.数学书第43页练习第1,2题;
2.不添加辅助线,直接运用平行四边形的定义, 证明其对角相等。
作业必做 △ABC是等腰三角形,AB=AC, P是底边BC
上一动点,PE∥AB,PF∥AC,点E,F分别在AC,AB
上.求证:PE+PF=AB.
