人教版六年级数学下册 6.4 数学思考(1)上课课件(共21张PPT)
文档属性
| 名称 | 人教版六年级数学下册 6.4 数学思考(1)上课课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 708.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-16 22:06:12 | ||
图片预览





文档简介
(共21张PPT)
专题4 数学思考
6.4 数学思考(1)
学习目标
掌握根据图形或数列找规律的方法。
学习重点
学习难点
根据图形或数列找规律。
能够用找规律方法解决问题。
一、引入新课
该怎么办呢?
请同学们在纸上任意画8个不在同一直线上的点。
这8个点一共可以连成多少条线段?
别着急,现在我们就来解决这个问题。
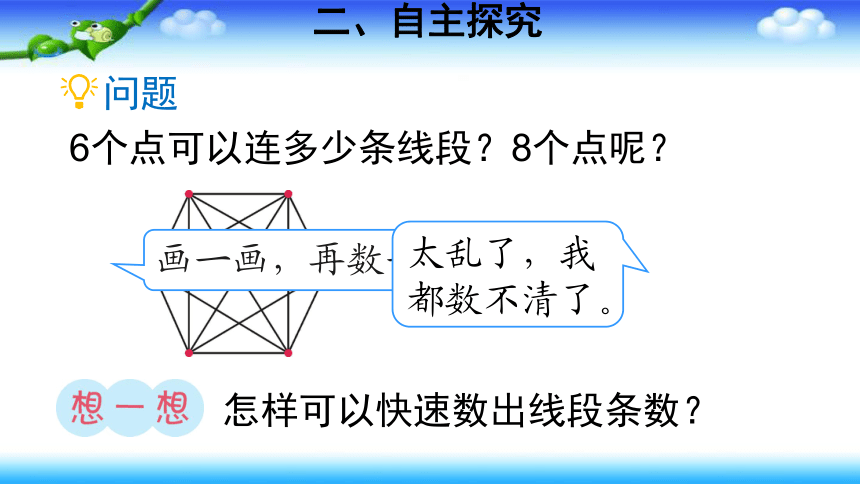
二、自主探究
6个点可以连多少条线段?8个点呢?
问题
画一画,再数一数。
太乱了,我都数不清了。
怎样可以快速数出线段条数?
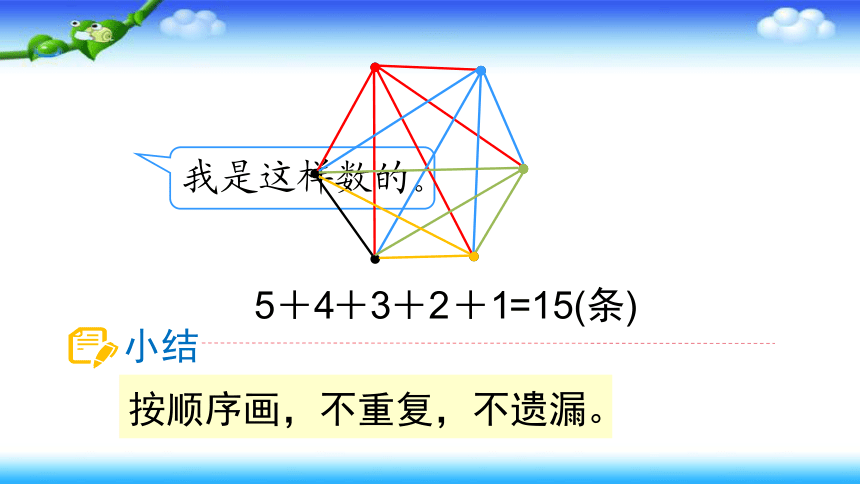
我是这样数的。
5
+4
+3
+2
+1
=15(条)
小结
按顺序画,不重复,不遗漏。
8个点连成的线段怎么数呢?有没有什么规律?
我们可以从2个点开始,逐步增加点数来研究。
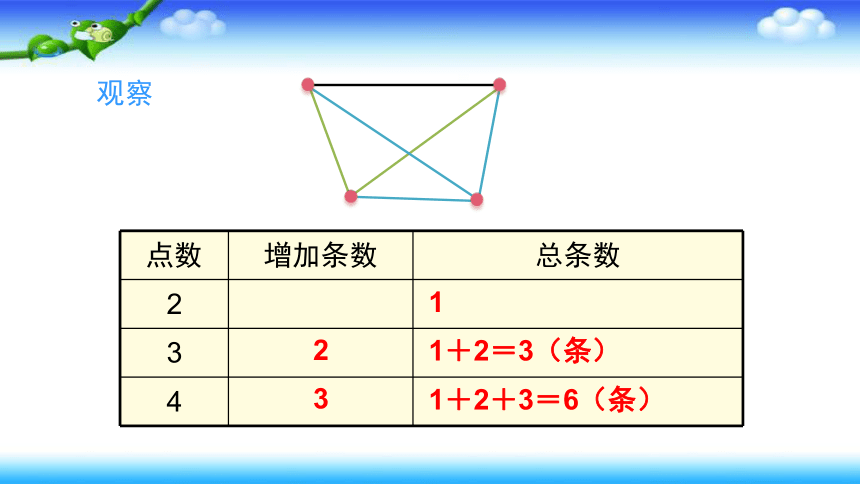
点数 增加条数 总条数
2
3
4
观察
1
2
1+2=3(条)
3
1+2+3=6(条)
发现
每次增加的线段条数比点数少1。
观察“点数”和“增加条数”,你发现了什么规律?
点数 2 3 4 …
增加条数 2 3 …
总条数 1 3 6 …
如果是5个点、6个点时,分别比上一次增加几条线段?
点数 增加条数 总条数
5
6
4
1+2+3+4=10(条)
5
1+2+3+4+5=15(条)
根据规律,8个点能连几条线段?
问题
1+2+3+4+5+6+7
能用简单方法计算吗?
= 28(条)
= 8×3+4
= (1+7)+(2+6)+(3+5)+4
为什么有8个点,列式却只加到7呢?
因为第8个点只能和前面的7个点分别连成线段,只能增加7条线段。
根据规律,你知道12个点、20个点能连多少条线段吗?
问题
1+2+3+4+5+6+7+8+9+10+11
= (1+11)+(2+10)+(3+9)+(4+8)
+(5+7)+6
= 66(条) ——12个点
= 12×5+6
=(1+19)+(2+18)+(3+17)+……
+(8+12)+(9+11)+10
=20×9+10
=190(条) ——20个点
1+2+3+4+5+6+……+19
按照简单的方法计算,你发现了什么,试着归纳一下。
n个点共连成线段:
1+2+3+4+5+6+…+(n-1)= n(n-1)
1
2
三、巩固深化
1.观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
每幅图各有多少个棋子?
1 4 9 16
在数的过程中,你发现了什么?
问题
1 4 9 16
1×1 2×2 3×3 4×4
每行的棋子数×行数=棋子总数
问题
1. 第7幅图有多少个棋子?第15幅图呢?
7×7=49(个)
15×15=225(个)
2. 每边的棋子数与图形的序号有什么关系?
相等
第n幅图每边有多少个棋子?一共有多少个棋子?
每行的棋子数×行数=棋子总数
n × n =棋子总数
n2 =棋子总数
四、课堂小结
2个点连成线段的条数:1(条)?
3个点连成线段的条数:1+2=3(条)?
4个点连成线段的条数:1+2+3=6(条)?
5个点连成线段的条数:1+2+3+4=10(条)?
n个点共连成线段:
1+2+3+4+5+6+…+(n-1)= n(n-1)
1
2
五、课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
六、教学反思
教学过程不是单纯地传授和学习知识的过程,而是促进学生全面发展的过程。本节课教学让学生在理解和掌握数学知识的过程中,不断运用各种思维方法和形式,如比较、分析、综合、推理、概括等,整个过程都在逐步地让学生学会“化难为易”的数学思想,采用合适的方法解决较复杂的数学问题。
专题4 数学思考
6.4 数学思考(1)
学习目标
掌握根据图形或数列找规律的方法。
学习重点
学习难点
根据图形或数列找规律。
能够用找规律方法解决问题。
一、引入新课
该怎么办呢?
请同学们在纸上任意画8个不在同一直线上的点。
这8个点一共可以连成多少条线段?
别着急,现在我们就来解决这个问题。
二、自主探究
6个点可以连多少条线段?8个点呢?
问题
画一画,再数一数。
太乱了,我都数不清了。
怎样可以快速数出线段条数?
我是这样数的。
5
+4
+3
+2
+1
=15(条)
小结
按顺序画,不重复,不遗漏。
8个点连成的线段怎么数呢?有没有什么规律?
我们可以从2个点开始,逐步增加点数来研究。
点数 增加条数 总条数
2
3
4
观察
1
2
1+2=3(条)
3
1+2+3=6(条)
发现
每次增加的线段条数比点数少1。
观察“点数”和“增加条数”,你发现了什么规律?
点数 2 3 4 …
增加条数 2 3 …
总条数 1 3 6 …
如果是5个点、6个点时,分别比上一次增加几条线段?
点数 增加条数 总条数
5
6
4
1+2+3+4=10(条)
5
1+2+3+4+5=15(条)
根据规律,8个点能连几条线段?
问题
1+2+3+4+5+6+7
能用简单方法计算吗?
= 28(条)
= 8×3+4
= (1+7)+(2+6)+(3+5)+4
为什么有8个点,列式却只加到7呢?
因为第8个点只能和前面的7个点分别连成线段,只能增加7条线段。
根据规律,你知道12个点、20个点能连多少条线段吗?
问题
1+2+3+4+5+6+7+8+9+10+11
= (1+11)+(2+10)+(3+9)+(4+8)
+(5+7)+6
= 66(条) ——12个点
= 12×5+6
=(1+19)+(2+18)+(3+17)+……
+(8+12)+(9+11)+10
=20×9+10
=190(条) ——20个点
1+2+3+4+5+6+……+19
按照简单的方法计算,你发现了什么,试着归纳一下。
n个点共连成线段:
1+2+3+4+5+6+…+(n-1)= n(n-1)
1
2
三、巩固深化
1.观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
每幅图各有多少个棋子?
1 4 9 16
在数的过程中,你发现了什么?
问题
1 4 9 16
1×1 2×2 3×3 4×4
每行的棋子数×行数=棋子总数
问题
1. 第7幅图有多少个棋子?第15幅图呢?
7×7=49(个)
15×15=225(个)
2. 每边的棋子数与图形的序号有什么关系?
相等
第n幅图每边有多少个棋子?一共有多少个棋子?
每行的棋子数×行数=棋子总数
n × n =棋子总数
n2 =棋子总数
四、课堂小结
2个点连成线段的条数:1(条)?
3个点连成线段的条数:1+2=3(条)?
4个点连成线段的条数:1+2+3=6(条)?
5个点连成线段的条数:1+2+3+4=10(条)?
n个点共连成线段:
1+2+3+4+5+6+…+(n-1)= n(n-1)
1
2
五、课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
六、教学反思
教学过程不是单纯地传授和学习知识的过程,而是促进学生全面发展的过程。本节课教学让学生在理解和掌握数学知识的过程中,不断运用各种思维方法和形式,如比较、分析、综合、推理、概括等,整个过程都在逐步地让学生学会“化难为易”的数学思想,采用合适的方法解决较复杂的数学问题。
