苏教版高中数学必修四教学讲义,复习补习资料(含典例分析,巩固练习):18《三角函数》全章复习与巩固(提高)word版含答案解析
文档属性
| 名称 | 苏教版高中数学必修四教学讲义,复习补习资料(含典例分析,巩固练习):18《三角函数》全章复习与巩固(提高)word版含答案解析 | 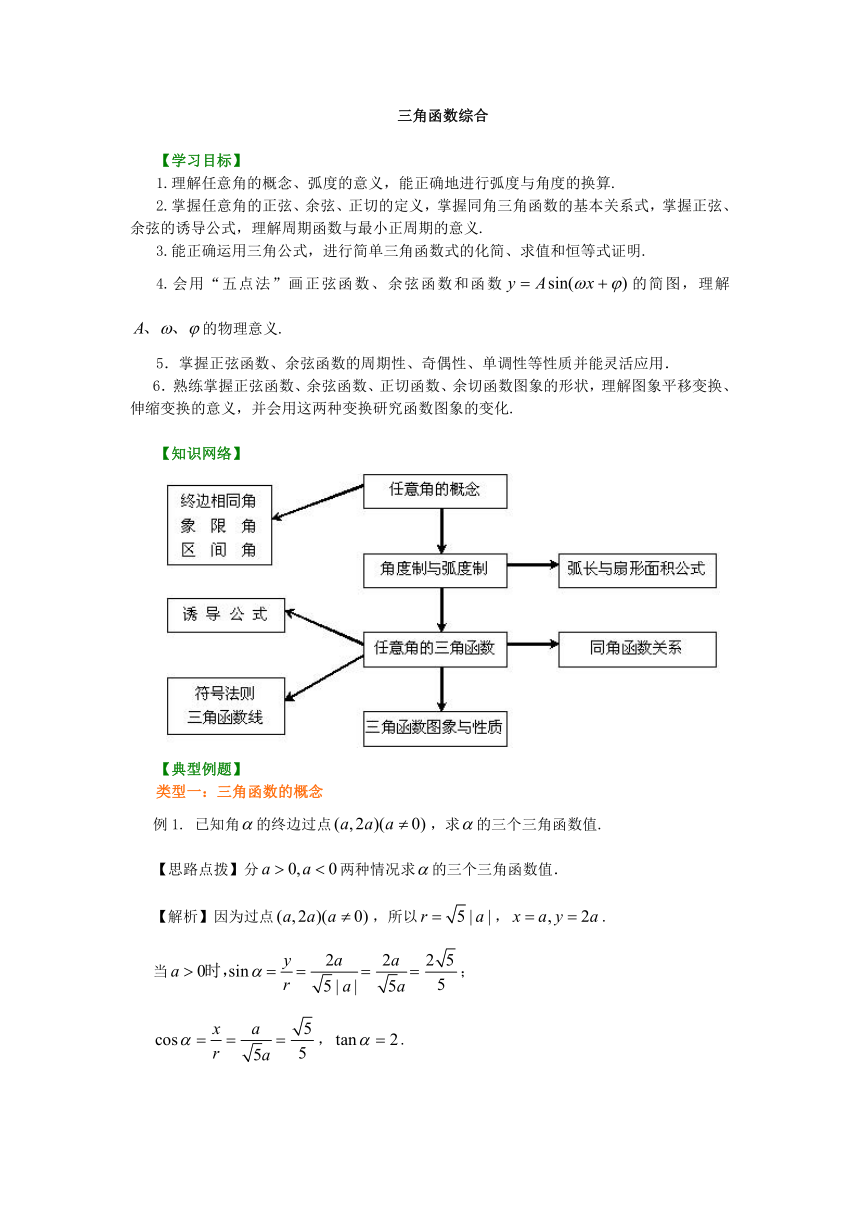 | |
| 格式 | zip | ||
| 文件大小 | 404.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 23:24:00 | ||
图片预览





文档简介
三角函数综合
【学习目标】
1.理解任意角的概念、弧度的意义,能正确地进行弧度与角度的换算.
2.掌握任意角的正弦、余弦、正切的定义,掌握同角三角函数的基本关系式,掌握正弦、余弦的诱导公式,理解周期函数与最小正周期的意义.
3.能正确运用三角公式,进行简单三角函数式的化简、求值和恒等式证明.
4.会用“五点法”画正弦函数、余弦函数和函数的简图,理解的物理意义.
5.掌握正弦函数、余弦函数的周期性、奇偶性、单调性等性质并能灵活应用.
6.熟练掌握正弦函数、余弦函数、正切函数、余切函数图象的形状,理解图象平移变换、伸缩变换的意义,并会用这两种变换研究函数图象的变化.
【知识网络】
【典型例题】
类型一:三角函数的概念
例1. 已知角的终边过点,求的三个三角函数值.
【思路点拨】分两种情况求的三个三角函数值.
【解析】因为过点,所以,.
当;
,.
当,;.
【总结升华】(1)当角的终边上点的坐标以参数形式给出时,要根据问题的实际及解题的需要对参数进行分类讨论;
(2)若角已经给定,不论点选在的终边上的什么位置,角的三角函数值都是确定的;另一方面,如果角终边上点坐标已经确定,那么根据三角函数定义,角的三角函数值也是确定的.
举一反三:
【变式1】已知角的终边上一点,且,求的值.
【解析】由题设知,,所以,得,
从而,
解得或.
当时,, ;
当时,, ;
当时,, .
类型二:扇形的弧长与面积的计算
例2.已知一半径为r的扇形,它的周长等于所在圆的周长的一半,那么扇形的中心角是多少弧度?合多少度?扇形的面积是多少?
【答案】
【解析】设扇形的圆心角是,因为扇形的弧长是,所以扇形的周长是
依题意,得
≈≈
【总结升华】弧长和扇形面积的核心公式是圆周长公式和圆面积公式,当用圆心角的弧度数代替时,即得到一般的弧长公式和扇形面积公式:
举一反三:
类型三:同角三角函数的基本关系式
例3.已知,求的值.
【思路点拨】由题意知,所以A为钝角,然后求出即可求得.
【解析】
方法一:由,得
又
由 得
方法二:由可得
即整理得
即
或,由已知知不合题意,舍去.
,两边平方得:,所以
【总结升华】同角三角函数基本关系是反映了各种三角函数之间的内在联系,为三角函数式的恒等变形提供了工具与方法.
举一反三:
【变式1】已知cosθ-sinθ= -, 求sinθcosθ,sinθ+cosθ的值.
【答案】
【解析】
,,
,
【变式2】证明:.
【证明】 [法1]——右到左,切化弦,由繁到简.
右左.
[法2](证与原式等价的式子)即证:.
左右.
类型四:三角函数的诱导公式
例4.已知sin(3π+θ)=,求的值.
【思路点拨】利用诱导公式,求出sin θ=-.然后化简要求的式子,即可求得结果.
【答案】18
【解析】 ∵sin(3π+θ)=-sin θ=,∴sin θ=-,
∴原式=
=
=+=
===18.
【总结升华】 诱导公式用角度和弧度制表示都成立,记忆方法可以概括为“奇变偶不变,符号看象限”,“变”与“不变”是相对于对偶关系的函数而言的,sin与cos对偶,“奇”、“偶”是对诱导公式中的整数k来讲的,象限指中,将看作锐角时,所在象限,如将写成,因为3是奇数,则“cos”变为对偶函数符号“sin”,又看作第四象限角,为“+”,所以有.
举一反三:
【变式1】已知函数f(x)=asin(πx+α)+bcos(πx+β),且f(2 009)=3,则f(2 010)的值是 ( )
A.-1 B.-2 C.-3 D.1
【答案】C
【解析】
f(2 009)=asin(2 009π+α)+bcos(2 009π+β)
=asin(π+α)+bcos(π+β)
=-asin α-bcos β=3.
∴asin α+bcos β=-3.
∴f(2 010)=asin(2 010π+α)+bcos(2 010π+β)
=asin α+bcos β=-3.
【变式2】化简(1)
(2).
【解析】(1)当n=4k(k∈Z)时,
当n=4k+1(k∈Z)时,
当n=4k+2(k∈Z)时,
当n=4k+3(k∈Z)时,
(2)①当时,
原式.
②当时,
原式.
【总结升华】关键抓住题中的整数是表示的整数倍与公式中的整数有区别,所以必须把分成奇数和偶数两种类型,分别加以讨论.
类型五:三角函数的图象和性质
例5. 函数的图象是( )
【答案】A
【解析】是偶函数,可排除B、D,由的值域可以确定.因此本题应选A.
举一反三:
【变式1】函数在内 ( )
A.没有零点 B.有且仅有一个零点
C.有且仅有两个零点 D.有无穷多个零点
【答案】B
例6.把函数y=cos2x+1的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图像是( )
【思路点拨】首先根据函数图象变换的公式,可得最终得到的图象对应的解析式为:y=cos(x+1),然后将曲线y=cos(x+1)的图象和余弦曲线y=cosx进行对照,可得正确答案.
【答案】A
【解析】将函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到的图象对应的解析式为:y=cosx+1,再将y=cosx+1图象向左平移1个单位长度,再向下平移?1个单位长度,得到的图象对应的解析式为:y=cos(x+1),∵曲线y=cos(x+1)由余弦曲线y=cosx左移一个单位而得,∴曲线y=cos(x+1)经过点和,且在区间上函数值小于0,由此可得,选项A正确,故选A.
举一反三:
【变式1】已知函数的最小正周期为,为了得到函数 的图象,只要将的图象( )
A. 向左平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向右平移个单位长度
【思路点拨】对于不同三角函数图象之间的平移变换,一定要根据诱导公式将二者之间变换清楚.
【答案】A
【解析】
由题知又,所以所以
=
=
显然将的图象向左平移个单位长度便可得到的图象.故选A.
例7.已知函数其中,
(I)若求的值;
(Ⅱ)在(I)的条件下,若函数的图像的相邻两条对称轴之间的距离等于,求函数的解析式;并求最小正实数,使得函数的图像象左平移个单位所对应的函数是偶函数.
【思路点拨】(1)把所给的式子化简,然后结合平方关系式得出,由,
,求出的值.(Ⅱ)由题意求得,,故,进一步求出的解析式.
【答案】(I)(Ⅱ)
【解析】
(I)由,得,得
又.
(Ⅱ)由(I)得,
依题意,
又故
函数的图像向左平移个单位后所对应的函数为
是偶函数当且仅当
即
从而,最小正实数
【总结升华】本题考查了同角三角函数的基本关系式及函数的性质,属中等难度题.
举一反三:
【变式1】已知函数(其中)的周期为,且图象上一个最低点为. w.w.w.k.s.5.u.c.o.m
(Ⅰ)求的解析式;(Ⅱ)当,求的最值.
【答案】(Ⅰ) (Ⅱ)最小值为1,最大值为.
【解析】(1)由最低点为
由
由点在图像上得即
又,
(Ⅱ)
.
【巩固练习】
1.函数的最小正周期是( )
A. B. C. D.
2.函数的零点个数是( )
A. B. C. D.
3.已知函数,那么下列命题中正确的是( )
A.是周期函数为的奇函数 B. 是周期为2的偶函数
C. 是周期为1的非奇非偶函数 D. 是周期为2的非奇非偶函数
4.已知函数的图象关于直线对称,则可能是( )
A. B. C. D.
5.函数在区间上的简图是( ) .
6.设是定义域为,最小正周期为的函数,若
则等于( )
A. B. C. D.
7.函数的最小值为( )
A. B. C. D.
8.设0A.sin(sinx)C.sin(tanx)9.函数的定义域为,则函数的定义域为__________________.
10.设,若函数在上单调递增,则的取值范围是________.
11.函数的定义域为________________.
12.如图所示,一个半径为3m的圆形水轮,水轮圆心O距水面2m,已知水轮每分钟绕圆心O逆时针旋转3圈.若点P从如图位置开始旋转(OP平行于水面),那么5s后点P到水面的距离为 m,试进一步写出点P到水面的距离与时间满足的函数关系式 .
13.已知,求下列各式的值:
(1);
(2)
14.已知函数f(x)=Asin(ωx+φ)+b (ω>0,|φ|<)的图象的一部分如图所示:
(1)求f(x)的表达式;
(2)试写出f(x)的对称轴方程.
15.是否存在角,其中,,使得等式
同时成立.若存在,求出的值;若不存在,请说明理由.
16.已知函数,的图象关于点对称,且在区间上是单调函数,求的值.
【答案与解析】
1.【答案】D
【解析】
2. 【答案】C
【解析】 在同一坐标系中分别作出函数的图象,左边三个交点,右边三个交点,再加上原点,共计个.
3.【答案】B
4. 【答案】C
【解析】对称轴经过最高点或最低点,
5.【答案】A
6. 【答案】B
【解析】
7.【答案】 B
【解析】令,则,对称轴,
是函数的递增区间,当时;
8. 【答案】A
【解析】当09. 【答案】
【解析】
10. 【答案】
【解析】令则是函数的关于
原点对称的递增区间中范围最大的,即,
则
11.【答案】
【解析】
12. 【答案】
【解析】每秒点P转过的角度为;秒后,P转过的角度为.
以水轮中心为原点,以水平方向为轴建立坐标系,所以水轮上任意一点P,其中为从水平位置逆时针转过的角度,即P,所以P到水面的距离.
13.【解析】由已知得
(1)=
(2)原式=
=
=
=.
14.【解析】 (1)由图象可知,函数的最大值M=3,
最小值m=-1,则A=
又,
∴,∴f(x)=2sin(2x+φ)+1,
将x=,y=3代入上式,得,
∴,k∈Z,
即φ=+2kπ,k∈Z,∴φ=,
∴f(x)=2sin+1.
(2)由2x+=+kπ,得x=+kπ,k∈Z,
∴f(x)=2sin+1的对称轴方程为
kπ,k∈Z.
15.【解析】假设满足题设要求的存在,则满足
(1)2+(2)2,得
即,
,或
(1)当时,由(2)得,
,
(2)当时,由(2)得,,但不适合(1)式,故舍去.
综上可知,存在使两个等式同时成立.
16.【解析】由,得因为,所以.
又的图象关于点对称,所以,即,
结合,可得,
当时,,在上是减函数;
当时,,在上是减函数;
当时,,在上不是单调函数;
所以,综上得或.
【学习目标】
1.理解任意角的概念、弧度的意义,能正确地进行弧度与角度的换算.
2.掌握任意角的正弦、余弦、正切的定义,掌握同角三角函数的基本关系式,掌握正弦、余弦的诱导公式,理解周期函数与最小正周期的意义.
3.能正确运用三角公式,进行简单三角函数式的化简、求值和恒等式证明.
4.会用“五点法”画正弦函数、余弦函数和函数的简图,理解的物理意义.
5.掌握正弦函数、余弦函数的周期性、奇偶性、单调性等性质并能灵活应用.
6.熟练掌握正弦函数、余弦函数、正切函数、余切函数图象的形状,理解图象平移变换、伸缩变换的意义,并会用这两种变换研究函数图象的变化.
【知识网络】
【典型例题】
类型一:三角函数的概念
例1. 已知角的终边过点,求的三个三角函数值.
【思路点拨】分两种情况求的三个三角函数值.
【解析】因为过点,所以,.
当;
,.
当,;.
【总结升华】(1)当角的终边上点的坐标以参数形式给出时,要根据问题的实际及解题的需要对参数进行分类讨论;
(2)若角已经给定,不论点选在的终边上的什么位置,角的三角函数值都是确定的;另一方面,如果角终边上点坐标已经确定,那么根据三角函数定义,角的三角函数值也是确定的.
举一反三:
【变式1】已知角的终边上一点,且,求的值.
【解析】由题设知,,所以,得,
从而,
解得或.
当时,, ;
当时,, ;
当时,, .
类型二:扇形的弧长与面积的计算
例2.已知一半径为r的扇形,它的周长等于所在圆的周长的一半,那么扇形的中心角是多少弧度?合多少度?扇形的面积是多少?
【答案】
【解析】设扇形的圆心角是,因为扇形的弧长是,所以扇形的周长是
依题意,得
≈≈
【总结升华】弧长和扇形面积的核心公式是圆周长公式和圆面积公式,当用圆心角的弧度数代替时,即得到一般的弧长公式和扇形面积公式:
举一反三:
类型三:同角三角函数的基本关系式
例3.已知,求的值.
【思路点拨】由题意知,所以A为钝角,然后求出即可求得.
【解析】
方法一:由,得
又
由 得
方法二:由可得
即整理得
即
或,由已知知不合题意,舍去.
,两边平方得:,所以
【总结升华】同角三角函数基本关系是反映了各种三角函数之间的内在联系,为三角函数式的恒等变形提供了工具与方法.
举一反三:
【变式1】已知cosθ-sinθ= -, 求sinθcosθ,sinθ+cosθ的值.
【答案】
【解析】
,,
,
【变式2】证明:.
【证明】 [法1]——右到左,切化弦,由繁到简.
右左.
[法2](证与原式等价的式子)即证:.
左右.
类型四:三角函数的诱导公式
例4.已知sin(3π+θ)=,求的值.
【思路点拨】利用诱导公式,求出sin θ=-.然后化简要求的式子,即可求得结果.
【答案】18
【解析】 ∵sin(3π+θ)=-sin θ=,∴sin θ=-,
∴原式=
=
=+=
===18.
【总结升华】 诱导公式用角度和弧度制表示都成立,记忆方法可以概括为“奇变偶不变,符号看象限”,“变”与“不变”是相对于对偶关系的函数而言的,sin与cos对偶,“奇”、“偶”是对诱导公式中的整数k来讲的,象限指中,将看作锐角时,所在象限,如将写成,因为3是奇数,则“cos”变为对偶函数符号“sin”,又看作第四象限角,为“+”,所以有.
举一反三:
【变式1】已知函数f(x)=asin(πx+α)+bcos(πx+β),且f(2 009)=3,则f(2 010)的值是 ( )
A.-1 B.-2 C.-3 D.1
【答案】C
【解析】
f(2 009)=asin(2 009π+α)+bcos(2 009π+β)
=asin(π+α)+bcos(π+β)
=-asin α-bcos β=3.
∴asin α+bcos β=-3.
∴f(2 010)=asin(2 010π+α)+bcos(2 010π+β)
=asin α+bcos β=-3.
【变式2】化简(1)
(2).
【解析】(1)当n=4k(k∈Z)时,
当n=4k+1(k∈Z)时,
当n=4k+2(k∈Z)时,
当n=4k+3(k∈Z)时,
(2)①当时,
原式.
②当时,
原式.
【总结升华】关键抓住题中的整数是表示的整数倍与公式中的整数有区别,所以必须把分成奇数和偶数两种类型,分别加以讨论.
类型五:三角函数的图象和性质
例5. 函数的图象是( )
【答案】A
【解析】是偶函数,可排除B、D,由的值域可以确定.因此本题应选A.
举一反三:
【变式1】函数在内 ( )
A.没有零点 B.有且仅有一个零点
C.有且仅有两个零点 D.有无穷多个零点
【答案】B
例6.把函数y=cos2x+1的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图像是( )
【思路点拨】首先根据函数图象变换的公式,可得最终得到的图象对应的解析式为:y=cos(x+1),然后将曲线y=cos(x+1)的图象和余弦曲线y=cosx进行对照,可得正确答案.
【答案】A
【解析】将函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到的图象对应的解析式为:y=cosx+1,再将y=cosx+1图象向左平移1个单位长度,再向下平移?1个单位长度,得到的图象对应的解析式为:y=cos(x+1),∵曲线y=cos(x+1)由余弦曲线y=cosx左移一个单位而得,∴曲线y=cos(x+1)经过点和,且在区间上函数值小于0,由此可得,选项A正确,故选A.
举一反三:
【变式1】已知函数的最小正周期为,为了得到函数 的图象,只要将的图象( )
A. 向左平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向右平移个单位长度
【思路点拨】对于不同三角函数图象之间的平移变换,一定要根据诱导公式将二者之间变换清楚.
【答案】A
【解析】
由题知又,所以所以
=
=
显然将的图象向左平移个单位长度便可得到的图象.故选A.
例7.已知函数其中,
(I)若求的值;
(Ⅱ)在(I)的条件下,若函数的图像的相邻两条对称轴之间的距离等于,求函数的解析式;并求最小正实数,使得函数的图像象左平移个单位所对应的函数是偶函数.
【思路点拨】(1)把所给的式子化简,然后结合平方关系式得出,由,
,求出的值.(Ⅱ)由题意求得,,故,进一步求出的解析式.
【答案】(I)(Ⅱ)
【解析】
(I)由,得,得
又.
(Ⅱ)由(I)得,
依题意,
又故
函数的图像向左平移个单位后所对应的函数为
是偶函数当且仅当
即
从而,最小正实数
【总结升华】本题考查了同角三角函数的基本关系式及函数的性质,属中等难度题.
举一反三:
【变式1】已知函数(其中)的周期为,且图象上一个最低点为. w.w.w.k.s.5.u.c.o.m
(Ⅰ)求的解析式;(Ⅱ)当,求的最值.
【答案】(Ⅰ) (Ⅱ)最小值为1,最大值为.
【解析】(1)由最低点为
由
由点在图像上得即
又,
(Ⅱ)
.
【巩固练习】
1.函数的最小正周期是( )
A. B. C. D.
2.函数的零点个数是( )
A. B. C. D.
3.已知函数,那么下列命题中正确的是( )
A.是周期函数为的奇函数 B. 是周期为2的偶函数
C. 是周期为1的非奇非偶函数 D. 是周期为2的非奇非偶函数
4.已知函数的图象关于直线对称,则可能是( )
A. B. C. D.
5.函数在区间上的简图是( ) .
6.设是定义域为,最小正周期为的函数,若
则等于( )
A. B. C. D.
7.函数的最小值为( )
A. B. C. D.
8.设0
10.设,若函数在上单调递增,则的取值范围是________.
11.函数的定义域为________________.
12.如图所示,一个半径为3m的圆形水轮,水轮圆心O距水面2m,已知水轮每分钟绕圆心O逆时针旋转3圈.若点P从如图位置开始旋转(OP平行于水面),那么5s后点P到水面的距离为 m,试进一步写出点P到水面的距离与时间满足的函数关系式 .
13.已知,求下列各式的值:
(1);
(2)
14.已知函数f(x)=Asin(ωx+φ)+b (ω>0,|φ|<)的图象的一部分如图所示:
(1)求f(x)的表达式;
(2)试写出f(x)的对称轴方程.
15.是否存在角,其中,,使得等式
同时成立.若存在,求出的值;若不存在,请说明理由.
16.已知函数,的图象关于点对称,且在区间上是单调函数,求的值.
【答案与解析】
1.【答案】D
【解析】
2. 【答案】C
【解析】 在同一坐标系中分别作出函数的图象,左边三个交点,右边三个交点,再加上原点,共计个.
3.【答案】B
4. 【答案】C
【解析】对称轴经过最高点或最低点,
5.【答案】A
6. 【答案】B
【解析】
7.【答案】 B
【解析】令,则,对称轴,
是函数的递增区间,当时;
8. 【答案】A
【解析】当0
【解析】
10. 【答案】
【解析】令则是函数的关于
原点对称的递增区间中范围最大的,即,
则
11.【答案】
【解析】
12. 【答案】
【解析】每秒点P转过的角度为;秒后,P转过的角度为.
以水轮中心为原点,以水平方向为轴建立坐标系,所以水轮上任意一点P,其中为从水平位置逆时针转过的角度,即P,所以P到水面的距离.
13.【解析】由已知得
(1)=
(2)原式=
=
=
=.
14.【解析】 (1)由图象可知,函数的最大值M=3,
最小值m=-1,则A=
又,
∴,∴f(x)=2sin(2x+φ)+1,
将x=,y=3代入上式,得,
∴,k∈Z,
即φ=+2kπ,k∈Z,∴φ=,
∴f(x)=2sin+1.
(2)由2x+=+kπ,得x=+kπ,k∈Z,
∴f(x)=2sin+1的对称轴方程为
kπ,k∈Z.
15.【解析】假设满足题设要求的存在,则满足
(1)2+(2)2,得
即,
,或
(1)当时,由(2)得,
,
(2)当时,由(2)得,,但不适合(1)式,故舍去.
综上可知,存在使两个等式同时成立.
16.【解析】由,得因为,所以.
又的图象关于点对称,所以,即,
结合,可得,
当时,,在上是减函数;
当时,,在上是减函数;
当时,,在上不是单调函数;
所以,综上得或.
