人教版六年级数学下册 6.4 数学思考(3)上课课件(共18张PPT)
文档属性
| 名称 | 人教版六年级数学下册 6.4 数学思考(3)上课课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-16 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
6.4 数学思考(3)
学习目标
1.理解掌握利用等式性质进行等量代换求图形代表的数值。
2.在交流探讨中,进一步感受数学的简洁美和问题解决策略的多样化,学会用数学思想方法解决问题。
学习重点
学习难点
学会用演绎推理的思想解决问题。
利用等式的性质进行等量代换。
一、引入新课
这些图形你们都见过吗?
见过,有三角形、正方形……
当它们变成数字时又会发生什么有趣的事呢,一起来看看!
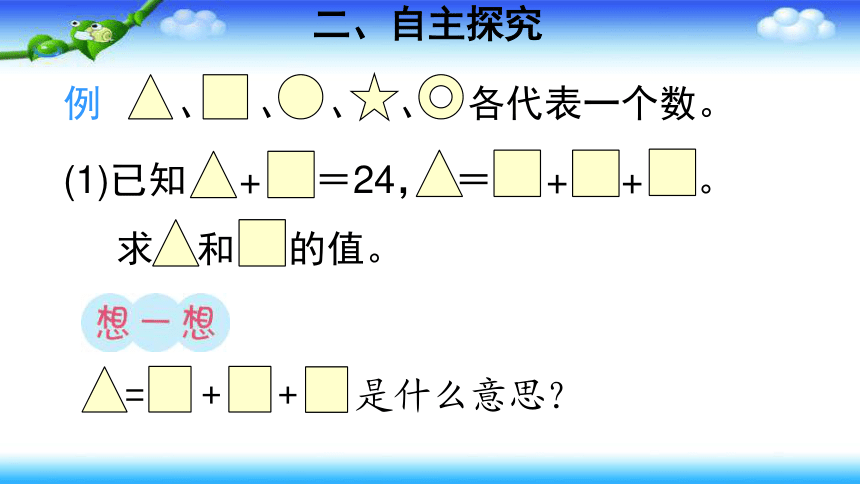
二、自主探究
、 、 、 、 各代表一个数。
例
(1)已知 + =24, = + + 。
求 和 的值。
= + + 是什么意思?
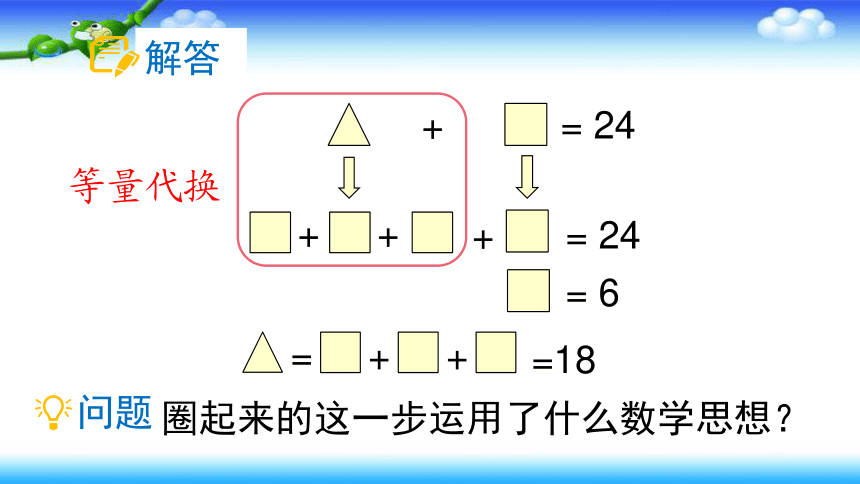
等量代换
+ = 24
= 6
+
= 24
+
+
=
+
+
=18
圈起来的这一步运用了什么数学思想?
解答
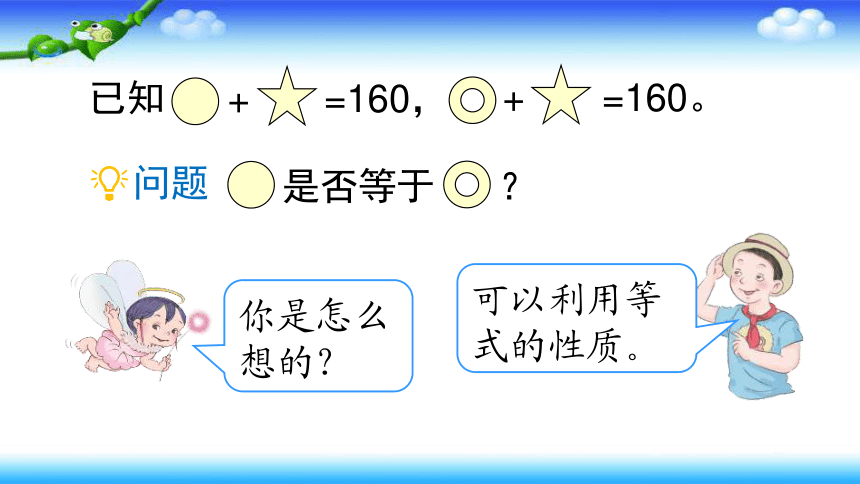
问题
你是怎么想的?
问题
是否等于 ?
+ =160,
+
=160。
已知
可以利用等式的性质。
解答
+ =160
+
=160
=160 -
=160 -
=
什么是平角?平角和直线有什么区别?
一条射线绕它的端点旋转,当始边和终边在同一条直线上,方向相反时,所构成的角叫平角。
小结
例 如右图,两条直线相交于点O。
每相邻两个角可以组成一个平角,一共能组成几个平角?
问题
自己动手数一数!
平角的两边在一条直线上。
∠1 和∠2、∠3 和∠4是平角;
小结
∠2 和∠3、∠1 和∠4是平角。
能组成4对平角。
例 如右图,两条直线相交于点O。
你能推出∠1=∠3吗?
问题
你是怎么想的?
∠1 和∠2、∠2 和∠3都能组成平角。
∠1+∠2=180°
∠2+∠3=180°
∠1=∠3
∠1 =180°-∠2
∠3 =180°-∠2
找等量关系
对看似不相关的独立的信息,在解决问题时怎样思考呢?
1
2
3
等量代换
合情推理
三、巩固深化
1.求图形代表的数。
(1)○+△=150 ○= 4×△
○=( ) △=( )
(2)○+□=31 △+○=20
□+△=39
○=( ) △=( )
□=( )
120
30
6
14
25
四、课堂小结
数学思考
等量代换
等式的性质
五、课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
六、教学反思
“数学思考”是总复习单元中的“另类”,它不仅是对以往所学知识的整理和复习,还在原有基础上有所提升与拓展。本节课的教学内容较为抽象难懂,所以在教学时要留给学生动手操作、合作学习的机会,使学生亲身体验探究等量代换的数学方法。
6.4 数学思考(3)
学习目标
1.理解掌握利用等式性质进行等量代换求图形代表的数值。
2.在交流探讨中,进一步感受数学的简洁美和问题解决策略的多样化,学会用数学思想方法解决问题。
学习重点
学习难点
学会用演绎推理的思想解决问题。
利用等式的性质进行等量代换。
一、引入新课
这些图形你们都见过吗?
见过,有三角形、正方形……
当它们变成数字时又会发生什么有趣的事呢,一起来看看!
二、自主探究
、 、 、 、 各代表一个数。
例
(1)已知 + =24, = + + 。
求 和 的值。
= + + 是什么意思?
等量代换
+ = 24
= 6
+
= 24
+
+
=
+
+
=18
圈起来的这一步运用了什么数学思想?
解答
问题
你是怎么想的?
问题
是否等于 ?
+ =160,
+
=160。
已知
可以利用等式的性质。
解答
+ =160
+
=160
=160 -
=160 -
=
什么是平角?平角和直线有什么区别?
一条射线绕它的端点旋转,当始边和终边在同一条直线上,方向相反时,所构成的角叫平角。
小结
例 如右图,两条直线相交于点O。
每相邻两个角可以组成一个平角,一共能组成几个平角?
问题
自己动手数一数!
平角的两边在一条直线上。
∠1 和∠2、∠3 和∠4是平角;
小结
∠2 和∠3、∠1 和∠4是平角。
能组成4对平角。
例 如右图,两条直线相交于点O。
你能推出∠1=∠3吗?
问题
你是怎么想的?
∠1 和∠2、∠2 和∠3都能组成平角。
∠1+∠2=180°
∠2+∠3=180°
∠1=∠3
∠1 =180°-∠2
∠3 =180°-∠2
找等量关系
对看似不相关的独立的信息,在解决问题时怎样思考呢?
1
2
3
等量代换
合情推理
三、巩固深化
1.求图形代表的数。
(1)○+△=150 ○= 4×△
○=( ) △=( )
(2)○+□=31 △+○=20
□+△=39
○=( ) △=( )
□=( )
120
30
6
14
25
四、课堂小结
数学思考
等量代换
等式的性质
五、课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
六、教学反思
“数学思考”是总复习单元中的“另类”,它不仅是对以往所学知识的整理和复习,还在原有基础上有所提升与拓展。本节课的教学内容较为抽象难懂,所以在教学时要留给学生动手操作、合作学习的机会,使学生亲身体验探究等量代换的数学方法。
