人教版八年级数学下册课件:20.2 数据的波动程度—方差 (共20张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:20.2 数据的波动程度—方差 (共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 226.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-16 00:00:00 | ||
图片预览





文档简介
课件20张PPT。20.2 数据的波动程度第1课时 方 差1.理解方差的概念及统计学意义;
2.会计算一组数据的方差; (重点)
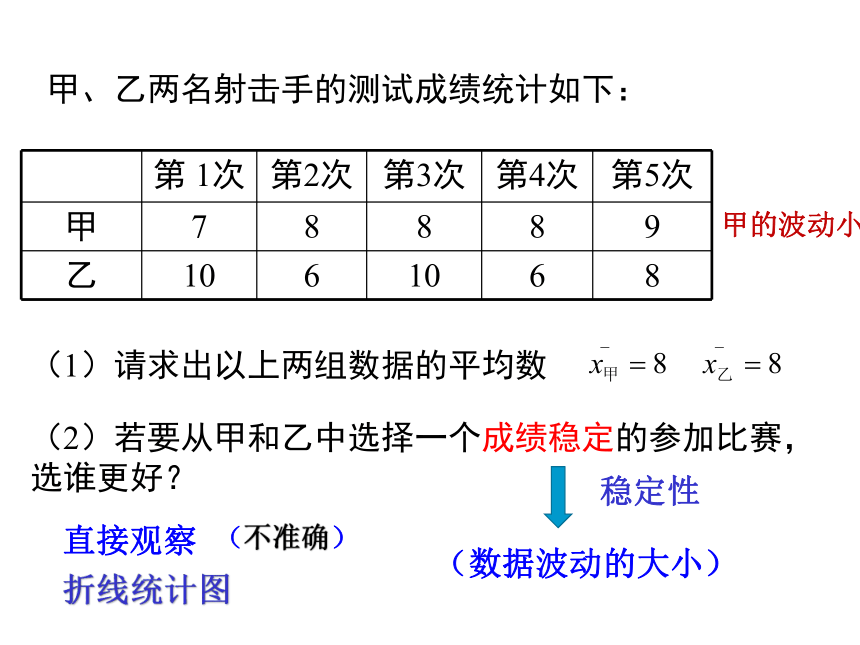
3.能够运用方差判断数据的波动程度,并解决简单的实际问题.(难点) 甲、乙两名射击手的测试成绩统计如下:(1)请求出以上两组数据的平均数(2)若要从甲和乙中选择一个成绩稳定的参加比赛,
选谁更好?(数据波动的大小)直接观察折线统计图(不准确)稳定性甲的波动小甲乙 稳定性
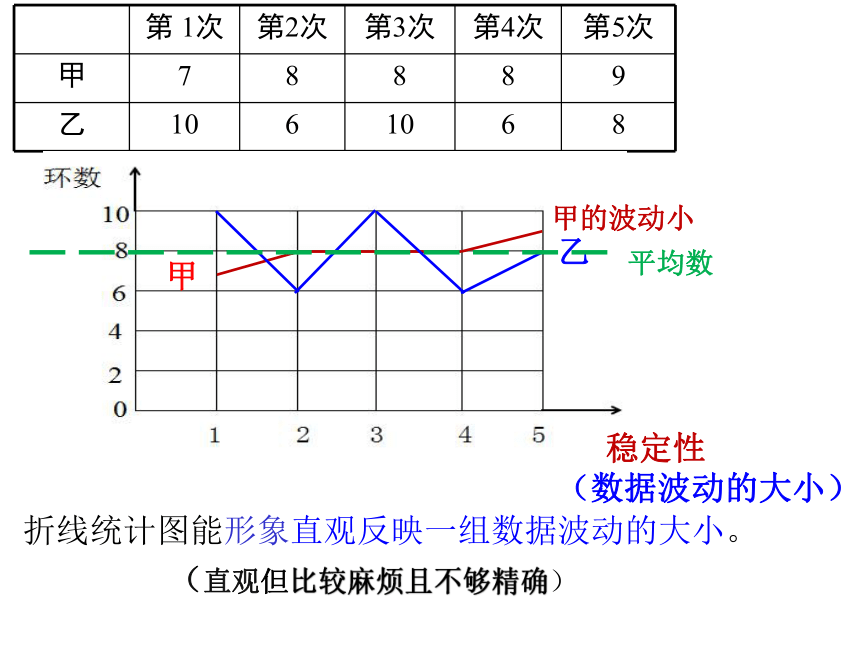
(数据波动的大小)折线统计图能形象直观反映一组数据波动的大小。(直观但比较麻烦且不够精确)平均数甲的波动小甲乙 稳定性
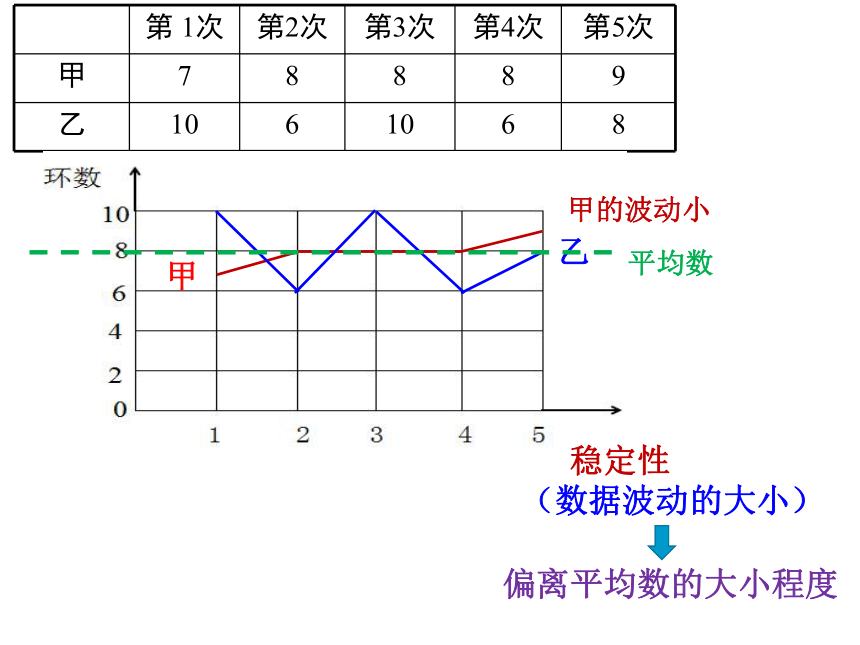
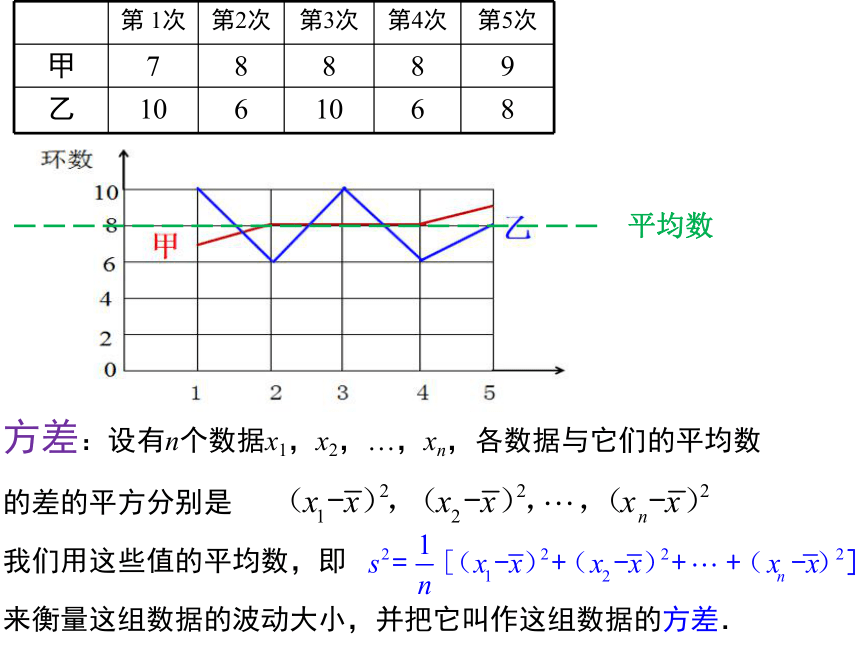
(数据波动的大小)平均数偏离平均数的大小程度甲的波动小平均数1、能用各个数据与平均数的差的和来表示数据偏离平均数的程度吗?试一试结果都为0各个数据与平均数的差的平方和方差再除以个数求出平均数平均数方差:设有n个数据x1,x2,…,xn,各数据与它们的平均数
的差的平方分别是
我们用这些值的平均数,即
来衡量这组数据的波动大小,并把它叫作这组数据的方差.方差:n个数据x1,x2,…,xn的方差结论:方差越大,说明数据的波动______,越______
方差越小,说明数据的波动______,越______越大不稳定越小稳定若要从甲和乙中选择一个成绩稳定的参加比赛,
选谁更好?(1)方差的计算公式
中, 10表示_____ , 数字20表示 _______. 平均数 练习数据个数
(2)人数相同的八年级(1)、(2)两班学生在同一次数学单元测试中,班级平均分和方差下:
, , ,则成绩较为稳定的班级是( )
A.甲班 B.乙班
C.两班成绩一样稳定 D.无法确定B大小稳定(3)体育课上,八1班两个组个10人参加立定跳远,要判断哪一组比较整齐,通常需要知道两个组立定跳远成绩的( )A.平均数 B.众数
C.方差 D.中位数C例:求数据2,3,4的方差练习: 求数据1,2,5,4的方差方差应用比较方差大小练习甲、乙两台编织机同时编织一种毛衣,在5天中,
两台编织机每天出的合格品数量如下(单位:件)
甲:10,8,7,7,8
乙:9, 8,7,7,9
(1)分别计算两人的平均数和方差
(2)在这5天中,哪台编织机出合格品的
波动较小?课堂小结方差方差的统计学意义(判断数据的波动程度):
方差越大(小),数据的波动越大(小).课后练习1.为了备战全国皮划艇马拉松赛,甲、乙运动员进行了艰苦的训练,他们在相同条件下各划艇10次的成绩的平均数相同,方差分别为0.23,0.20,则成绩较为稳定的是_______(选填“甲”或“乙”)2.方差的作用是( )
A. 表示数据的平均水平 B.表示数据的集中趋势
B. 表示数据的位置 D.表示数据的波动大小乙D(A组)3.甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:某同学分析上表后得出如下结论:①甲、乙两班学生成绩平均水平相同;②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);③甲班成绩的波动比乙班大.上述结论正确的有 .①②③ 4.甲、乙两小组各5名学生进行英语口语会话,各练习5次,他们每位同学的合格次数如下表:
(1) 求分别两人平均成绩和方差。
(2) 哪组的成绩比较整齐?
(B组)作业:(A组)1. 课本P128第1题
2.《学考精练》自主学习第1、2题
(B组)《学考精练》课时达标第2、3题
2.会计算一组数据的方差; (重点)
3.能够运用方差判断数据的波动程度,并解决简单的实际问题.(难点) 甲、乙两名射击手的测试成绩统计如下:(1)请求出以上两组数据的平均数(2)若要从甲和乙中选择一个成绩稳定的参加比赛,
选谁更好?(数据波动的大小)直接观察折线统计图(不准确)稳定性甲的波动小甲乙 稳定性
(数据波动的大小)折线统计图能形象直观反映一组数据波动的大小。(直观但比较麻烦且不够精确)平均数甲的波动小甲乙 稳定性
(数据波动的大小)平均数偏离平均数的大小程度甲的波动小平均数1、能用各个数据与平均数的差的和来表示数据偏离平均数的程度吗?试一试结果都为0各个数据与平均数的差的平方和方差再除以个数求出平均数平均数方差:设有n个数据x1,x2,…,xn,各数据与它们的平均数
的差的平方分别是
我们用这些值的平均数,即
来衡量这组数据的波动大小,并把它叫作这组数据的方差.方差:n个数据x1,x2,…,xn的方差结论:方差越大,说明数据的波动______,越______
方差越小,说明数据的波动______,越______越大不稳定越小稳定若要从甲和乙中选择一个成绩稳定的参加比赛,
选谁更好?(1)方差的计算公式
中, 10表示_____ , 数字20表示 _______. 平均数 练习数据个数
(2)人数相同的八年级(1)、(2)两班学生在同一次数学单元测试中,班级平均分和方差下:
, , ,则成绩较为稳定的班级是( )
A.甲班 B.乙班
C.两班成绩一样稳定 D.无法确定B大小稳定(3)体育课上,八1班两个组个10人参加立定跳远,要判断哪一组比较整齐,通常需要知道两个组立定跳远成绩的( )A.平均数 B.众数
C.方差 D.中位数C例:求数据2,3,4的方差练习: 求数据1,2,5,4的方差方差应用比较方差大小练习甲、乙两台编织机同时编织一种毛衣,在5天中,
两台编织机每天出的合格品数量如下(单位:件)
甲:10,8,7,7,8
乙:9, 8,7,7,9
(1)分别计算两人的平均数和方差
(2)在这5天中,哪台编织机出合格品的
波动较小?课堂小结方差方差的统计学意义(判断数据的波动程度):
方差越大(小),数据的波动越大(小).课后练习1.为了备战全国皮划艇马拉松赛,甲、乙运动员进行了艰苦的训练,他们在相同条件下各划艇10次的成绩的平均数相同,方差分别为0.23,0.20,则成绩较为稳定的是_______(选填“甲”或“乙”)2.方差的作用是( )
A. 表示数据的平均水平 B.表示数据的集中趋势
B. 表示数据的位置 D.表示数据的波动大小乙D(A组)3.甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:某同学分析上表后得出如下结论:①甲、乙两班学生成绩平均水平相同;②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);③甲班成绩的波动比乙班大.上述结论正确的有 .①②③ 4.甲、乙两小组各5名学生进行英语口语会话,各练习5次,他们每位同学的合格次数如下表:
(1) 求分别两人平均成绩和方差。
(2) 哪组的成绩比较整齐?
(B组)作业:(A组)1. 课本P128第1题
2.《学考精练》自主学习第1、2题
(B组)《学考精练》课时达标第2、3题
