人教版八年级数学下册课件:19.1.2 函数的图象(共20张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:19.1.2 函数的图象(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 188.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 16:09:48 | ||
图片预览






文档简介
课件20张PPT。第十九章 一次函数
19.1.2 函数的图象 一般地,在一个变化过程中,如果有 个变量 x 与y,并且对于 x 的每一个确定的值,y 都有 的值与其对应,那么我们就说 x 是 ,y 是 x 的 .1.函数的定义: 如果当 x =a 时,对应的 y =b,那么b 叫做当自变量的值为 a 时的 . 温故知新两唯一确定自变量函数值二、导入新课 我们先来思考这样一个问题:正方形的边长x与面积S的 关系为 ,
其中 x的取值范围是 。因为x表示的实际含义是正方形的边长,
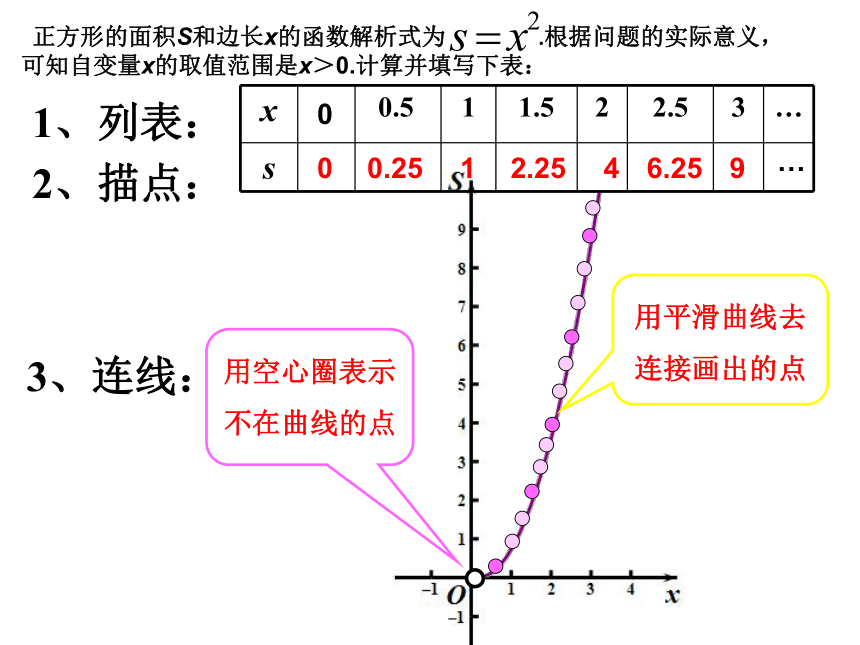
边长只能为正。你能解释x>0这个范围是怎样确定的吗?函数自变量3x > 0 正方形的面积S和边长x的函数解析式为 .根据问题的实际意义,可知自变量x的取值范围是x>0.计算并填写下表:1、列表:2、描点:3、连线:用平滑曲线去连接画出的点用空心圈表示不在曲线的点10.25492.256.2500…归纳一:函数的图象 一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
作用:
通过图象,我们可以数形结合地研究函数.
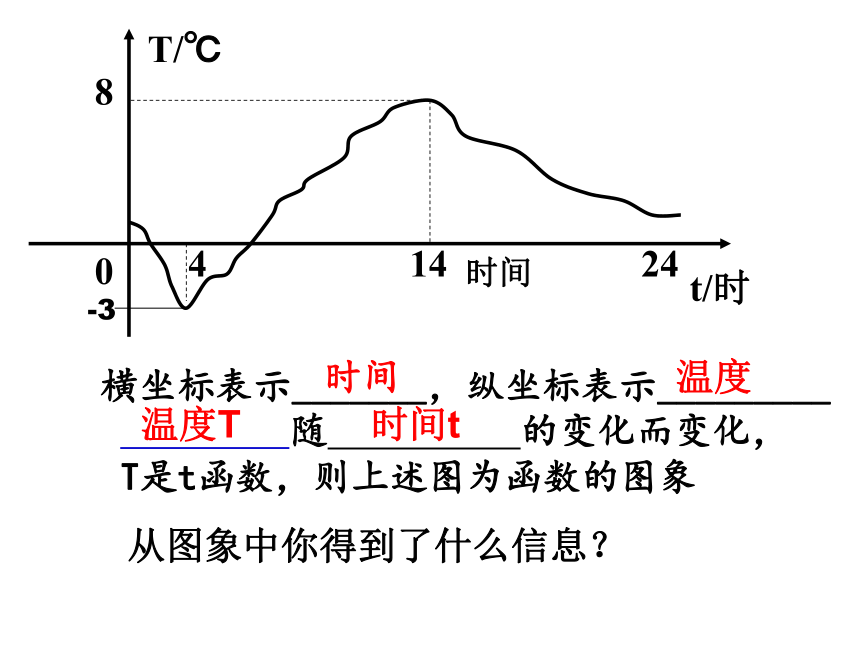
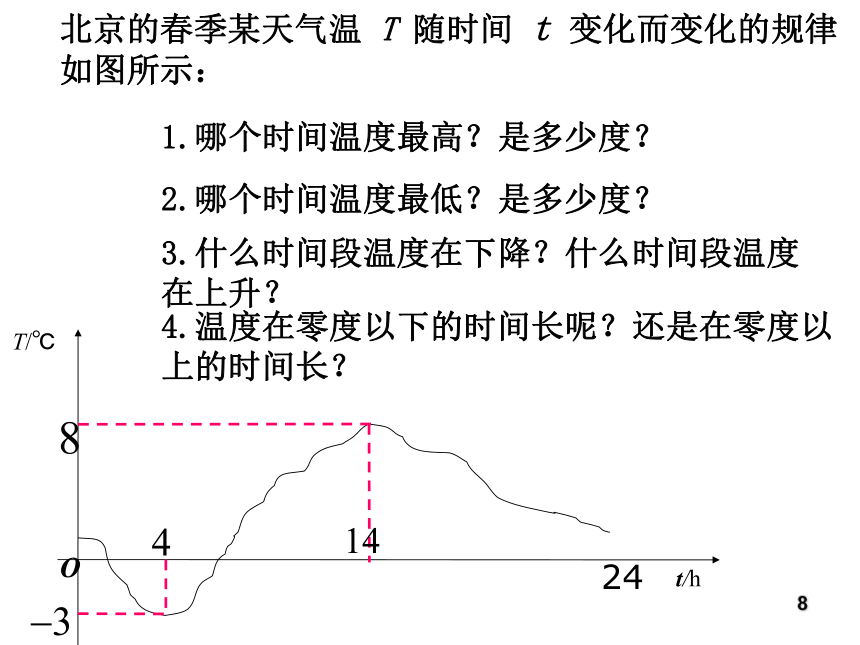
可以给我们带来许多信息。活动一: 根据函数图像回答问题 下图是自动测温仪记录的图象,它反映了北京的春季某天气温T如何随时间t的变化而变化。你从图象中得到了哪些信息?6横坐标表示_______,纵坐标表示_________ 随 的变化而变化,T是t函数,则上述图为函数的图象-3时间温度时间温度T时间t从图象中你得到了什么信息?T/℃北京的春季某天气温 T 随时间 t 变化而变化的规律如图所示:Ot/h248 活动结论: 1.我们可以从图象中直观看出一天中气温变化情况及任一时刻的气温大约是多少. 2.如果长期观察这样的气温图象,我们就能得到更多信息,掌握更多气温变化规律.9 识图策略: 1.了解横,纵轴的意义 2.从图像形状上观察图形的变化趋势。 3.抓住特殊点的实际意义。 好方法 例2如图,小明家、食堂、图书馆在同一条直
线上,小明从家去食堂吃早餐,接着去图书馆读报,
然后回家.下图反映了这个过程中,小明离他家的距
离y与时间x之间的对应关系.825285868x/分 0.8 0.6 y/千米 O 根据图象回答下列问题:
(1)食堂离小明家多远?小明从家到食堂用了多少时间?学以致用825285868x/min 0.8 0.6 y/km O 根据图象回答下列问题:
(2)小明吃早餐用了多少时间? (3)食堂离图书馆多远?小明从食 堂到图书馆用了多少时间?
825285868x/min 0.8 0.6 y/km O 根据图象回答下列问题:
(4)小明读报用了多长时间?
(5)图书馆离小明家多远?小明从图书馆回家的平均速度是多少? 活动三:在下列式子中,对于x的每个确定的值,y有唯一的对应值,即y是x的函数.请画出下列函数的图象.
1.y=x+0.5 分析:从式子y=x+0.5可以看出,x取任意实数时这个式子都有意义,所以x的取值范围是全体实数.-2.5-1.53.5解:
3、连线函数图象的画法1、列表2、描点列出自变量与函数的对应值表。
注意:自变量的值(满足取值范围),并取值要适当,以便画图.建立直角坐标系,以自变量的值为横坐标,
相应的函数值为纵坐标,描出表格中数值
对应的各点按照横坐标从小到大的顺序把描出的点用
平滑曲线依次连接起来归纳二:注:函数图象可能是曲线,也可能是直线,也可能是线段或射线,函数图象的形状取决于函数关系和自变量的取值范围。趣味思考,挑战自我龟兔赛跑小故事
领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但已经来不及了,乌龟先到达了终点………现在用S1 和S2 分别表示乌龟、兔子所走的路程,t为时间,请同学们画出与故事情节相吻合的大致图象巩固练习教课书第79页第2题课堂总结通过这节课的学习你有什么收获?一、函数的图象的意义:二、函数图象的画法:三、从函数图象中获取有用的信息列表、描点、连线 一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的图象。
小结与作业作业:教科书习题19.1 第6题,第8题,第9题。
19.1.2 函数的图象 一般地,在一个变化过程中,如果有 个变量 x 与y,并且对于 x 的每一个确定的值,y 都有 的值与其对应,那么我们就说 x 是 ,y 是 x 的 .1.函数的定义: 如果当 x =a 时,对应的 y =b,那么b 叫做当自变量的值为 a 时的 . 温故知新两唯一确定自变量函数值二、导入新课 我们先来思考这样一个问题:正方形的边长x与面积S的 关系为 ,
其中 x的取值范围是 。因为x表示的实际含义是正方形的边长,
边长只能为正。你能解释x>0这个范围是怎样确定的吗?函数自变量3x > 0 正方形的面积S和边长x的函数解析式为 .根据问题的实际意义,可知自变量x的取值范围是x>0.计算并填写下表:1、列表:2、描点:3、连线:用平滑曲线去连接画出的点用空心圈表示不在曲线的点10.25492.256.2500…归纳一:函数的图象 一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
作用:
通过图象,我们可以数形结合地研究函数.
可以给我们带来许多信息。活动一: 根据函数图像回答问题 下图是自动测温仪记录的图象,它反映了北京的春季某天气温T如何随时间t的变化而变化。你从图象中得到了哪些信息?6横坐标表示_______,纵坐标表示_________ 随 的变化而变化,T是t函数,则上述图为函数的图象-3时间温度时间温度T时间t从图象中你得到了什么信息?T/℃北京的春季某天气温 T 随时间 t 变化而变化的规律如图所示:Ot/h248 活动结论: 1.我们可以从图象中直观看出一天中气温变化情况及任一时刻的气温大约是多少. 2.如果长期观察这样的气温图象,我们就能得到更多信息,掌握更多气温变化规律.9 识图策略: 1.了解横,纵轴的意义 2.从图像形状上观察图形的变化趋势。 3.抓住特殊点的实际意义。 好方法 例2如图,小明家、食堂、图书馆在同一条直
线上,小明从家去食堂吃早餐,接着去图书馆读报,
然后回家.下图反映了这个过程中,小明离他家的距
离y与时间x之间的对应关系.825285868x/分 0.8 0.6 y/千米 O 根据图象回答下列问题:
(1)食堂离小明家多远?小明从家到食堂用了多少时间?学以致用825285868x/min 0.8 0.6 y/km O 根据图象回答下列问题:
(2)小明吃早餐用了多少时间? (3)食堂离图书馆多远?小明从食 堂到图书馆用了多少时间?
825285868x/min 0.8 0.6 y/km O 根据图象回答下列问题:
(4)小明读报用了多长时间?
(5)图书馆离小明家多远?小明从图书馆回家的平均速度是多少? 活动三:在下列式子中,对于x的每个确定的值,y有唯一的对应值,即y是x的函数.请画出下列函数的图象.
1.y=x+0.5 分析:从式子y=x+0.5可以看出,x取任意实数时这个式子都有意义,所以x的取值范围是全体实数.-2.5-1.53.5解:
3、连线函数图象的画法1、列表2、描点列出自变量与函数的对应值表。
注意:自变量的值(满足取值范围),并取值要适当,以便画图.建立直角坐标系,以自变量的值为横坐标,
相应的函数值为纵坐标,描出表格中数值
对应的各点按照横坐标从小到大的顺序把描出的点用
平滑曲线依次连接起来归纳二:注:函数图象可能是曲线,也可能是直线,也可能是线段或射线,函数图象的形状取决于函数关系和自变量的取值范围。趣味思考,挑战自我龟兔赛跑小故事
领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但已经来不及了,乌龟先到达了终点………现在用S1 和S2 分别表示乌龟、兔子所走的路程,t为时间,请同学们画出与故事情节相吻合的大致图象巩固练习教课书第79页第2题课堂总结通过这节课的学习你有什么收获?一、函数的图象的意义:二、函数图象的画法:三、从函数图象中获取有用的信息列表、描点、连线 一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的图象。
小结与作业作业:教科书习题19.1 第6题,第8题,第9题。
