人教版八年级数学下册 课件:19.2.1 正比例函数 (共25张PPT)
文档属性
| 名称 | 人教版八年级数学下册 课件:19.2.1 正比例函数 (共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 16:14:55 | ||
图片预览








文档简介
课件25张PPT。19.2 一次函数19.2.1 正比例函数学习目标1.掌握正比例函数的概念.
2.弄清正比例函数解析式中字母的意义.
3.会求正比例函数的解析式. 问题1:媒体报道:2014年3月8日0点41分由吉隆坡起飞前往北京的马航MH370,凌晨2点40分起,航班与地面失去联系,机上有154名中国人。 问题研讨(1)吉隆坡到北京约4500km,飞机速度900km/h,请问原计划几小时到达北京?(2)假设飞机一直在飞行,航行路程y(单位:km)与飞行时间x (单位:h)之间有什么关系?4500÷900=5(h)y=900x (0≤x≤5)(3)该航班由吉隆坡起飞2.5 h后,是否已经飞出马来西亚境外2 100 km的越南监测站?当x=2.5时,y=900×2.5=2250>2100,2.5 h后,已经飞出马来西亚境外2 100 km的越南监测站活动一:情境创设思考下列问题:
1. y=900x中,变量和常量分别是什么?其对应关系式是函数关系吗?谁是自变量,谁是函数?
2.自变量与常量按什么运算符号连接起来的?
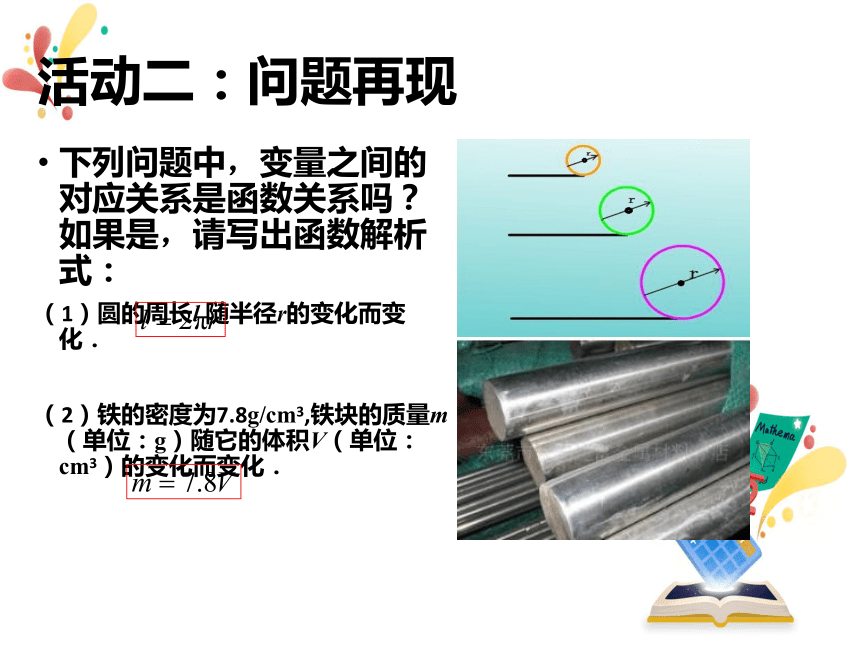
3.(1)与(2)之间有何联系?(2)与(3)呢?活动二:问题再现下列问题中,变量之间的对应关系是函数关系吗?如果是,请写出函数解析式:
(1)圆的周长l 随半径r的变化而变化.
(2)铁的密度为7.8g/cm3,铁块的质量m(单位:g)随它的体积V(单位:cm3)的变化而变化.
活动二:问题再现 (3)每个练习本的厚度为0.5cm,
一些练习本摞在一起的总厚度h
(单位:cm)随练习本的本数n的
变化而变化.
(4)冷冻一个0°C的物体,使它每
分钟下降2°C,物体温度T(单位:°C)
随冷冻时间t(单位:min)的变化而变
化.
活动二:问题再现问题探究:在 、 、 和
中 :
(1)以上对应关系都是函数关系吗?其变量和常量分别是什么?进一步指出谁是自变量,谁是函数?
(2)认真观察自变量和常量运用什么运算符号连接起来的?这些变量可以取哪些值?
(3)这4个函数表达式与问题1的函数表达式 y=900x有何共同特征?请你用语言加以描述.活动三:形成概念1.如果我们把这个常数记为k,你能用数学式子表达吗?
y=kx
2.对这个常数k有何要求呢?为什么?
k≠0
3.请你尝试给这类特殊函数下个定义:
形如 y=kx(k≠0)的函数,叫做正比例函数,其中k叫比例系数
4.这个函数表达式在形式上一个单项式还是多项式?你能指出它的系数是什么?次数为多少?
形式上是一个一次单项式,单项式系数就是比例系数k活动三:形成概念5.正比例函数y=kx(常数k≠0)的自变量x的取值范围是什么?这与问题1和思考的(1)~(4)的函数自变量的取值范围有何不同?
一般情况下正比例函数自变量取值范围为一切实数,但在特殊情况下自变量取值范围会有所不同
6.如何理解y与x成正比例函数?反之,y=kx(k为常数, k≠0)表示什么意义?
y与x成正比例函数 y=kx(常数k≠0)活动三:形成概念7.在正比例函数y=kx(k为常数,k≠0)中关键是确定哪个量?比例系数k一经确定,正比例函数确定了吗?怎样确定k呢?
从函数关系看,关键是比例系数k,比例系数k一确定,正比例函数就确定了;只需知道两个变量x、y的一对对应值即可确定k值.
从方程角度看,如果三个量x、y、k中已知其中两个量,则一定可以求出第三个量. 活动四:辨析概念1.下列式子,哪些表示y是x的正比例函数?如果是,请你指出正比例系数k的值.
(1)y=-0.1x (2)
(3)y=2x2 (4)y2=4x
(5)y=-4x+3 (6)y=2(x-x2 )+2x2 是正比例函数,
正比例系数为-0.1是正比例函数,
正比例系数为0.5不是正比例函数不是正比例函数不是正比例函数是正比例函数,正比例系数为2判定一个函数是否是正比例函数,要从化简后来判断!活动四:辨析概念2.列式表示下列问题中y与x的函数关系,并指出哪些是正比例函数.
(1)正方形的边长为xcm,周长为ycm.
y=4x 是正比例函数
(2)某人一年内的月平均收入为x元,他这年(12个月)的总收入为y元.
y=12x 是正比例函数
(3)一个长方体的长为2cm,宽为1.5cm,高为xcm ,体积为ycm3.
y=3x 是正比例函数
活动五:判定正误下列说法正确的打“√”,错误的打“×”
(1)若y=kx,则y是x的正比例函数( )
(2)若y=2x2,则y是x的正比例函数( )
(3)若y=2(x-1)+2,则y是x的正比例函数( )
(4)若y=2(x-1) ,则y是x-1的正比例函数( )
××√在特定条件下自变量可能不单独就是x了,要注意自变量的变化√例:已知y与x成正比例,当x=4时,y=8,试求y与x的函数解析式解:设所求的正比例函数解析式为:y=kx把x=4,y=8代入上式得:8=4k 解得k=2∴y与x的函数解析式为:y=2x活动六:待定系数法求正比例函数解析式 正比例函数y=kx中,当x=2时,
y=10,则它的解析式是_________. 若一个正比例函数的比例系数是4,
则它的解析式是__________.y = 4xy = 5x必做题活动六:应用新知已知正比例函数y=2x中,
(1)若0< y <10,则x的取值范围为_________.
(2)若-6< x <10,则y的取值范围为_________.0< <10-6< <100(1)写出△ABC的面积y(cm2)与高线x的函数解析式,并指明它是什么函数;
(2)当x=7时,求出y的值。(2)当x=7时,y=4×7=28活动六:应用新知
例3已知y与x-1成正比例,x=8时,y=6,写出y与x之间函数关系式,并分别求出x=4和x=-3时y的值。活动七: 变式应用 已知y与x+2 成正比例,当x=4时,y=12,那么当x=5时,y=______.解:∵ y与x+2 成正比例∴y=k(x+2)∵当x=4时,y=12∴12=k(4+2)解得:k=2∴y=2x+4∴当x=5时,y=1414活动七: 变式练习必做题 已知y=y1+y2,y1与x2成正比例,y2与x-2成正比例,当x=1时,y=0,当x=-3时,y=4,求x=3时,y的值。选做题活动八:课堂小结与作业布置你如何理解正比例函数的意义?能从哪几个方面去认识正比例函数?
1.从语言描述看:
函数关系式是常量与自变量的乘积.
2.从外形特征看:
(1)一般情况下y=kx(常数k≠0);
(2)在特定条件下自变量可能不单独是x了,要注意问题中自变量的变化.
3.从结果形式看:
函数表达式要化简后才能确认为正比例函数活动八:课堂小结与作业布置
4.从函数关系看:
比例系数k一确定,正比例函数就确定;必须知道两个变量x、y的一对对应值即可确定k.
5.从方程角度看:
如果三个量x、y、k中已知其中两个量,则一定可以求出第三个量.
6.求正比例函数解析式的两种方法:
(1)直接根据已知的比例系数求出解析式
(2)待定系数法 某学校准备添置一批篮球,已知所购篮球的总价y(元)与个数x(个)成正比例,当x=4(个)时,y=100(元)。
(1)求正比例函数关系式及自变量的取值范围;
(2)求当x=10(个)时,函数y的值;
(3)求当y=500(元)时,自变量x的值。解(1)设所求的正比例函数的解析式为y=kx,(2)当x=10(个)时,y=25x=25×10=250(元)。∵当x =4时,y =100,∴100=4k。解得 k= 25。∴所求正比例函数的解析式是y=25x。自变量x的取值范围是所有自然数。 1.下图表示江山到礼贤主要停靠站之间路程的千米数。一辆满载礼贤乘客的中巴车于上午8:00整从江山开往礼贤,已知中巴车行驶的路程S(千米)与时间t(分)成正比例(途中不停车),当t=4(分)时,S=2千米。问:(1)正比例函数的解析式;
(2)从8:30到8:40,该中巴车行驶在哪一段公路上;
(3)从何时到何时,该车行使在淤头至礼贤这段公路上。江山贺村淤头礼贤14千米6千米2千米 下图表示江山到礼贤主要停靠站之间路程的千米数。一辆满载礼贤乘客的中巴车于上午8:00整从江山开往礼贤,已知中巴车行驶的路程S(千米)与时间t(分)成正比例(途中不停车),当t=4(分)时,S=2千米。问:(1)正比例函数的解析式;
(2)从8:30到8:40,该中巴车行驶在哪一段公路上;
(3)从何时到何时,该车行使在淤头至礼贤这段公路上。江山贺村淤头礼贤14千米6千米2千米解(1)设所求的正比例函数的解析式为S=k t,(2)由已知得30≤t≤40,把t =4,S =2代入,得 2=4t。解得 k= 0.5 。所以,所求的正比例函数的解析式是S=0.5t。∴ 30≤2S≤40即15 ≤S≤20。由图可知中巴车行使在贺村至淤头公路上。(3)由已知得20≤S≤22,∴ 20≤0.5t≤22即40≤t≤44。所以从8:40至8:44,该车行使在淤头至礼贤公路上。
2.弄清正比例函数解析式中字母的意义.
3.会求正比例函数的解析式. 问题1:媒体报道:2014年3月8日0点41分由吉隆坡起飞前往北京的马航MH370,凌晨2点40分起,航班与地面失去联系,机上有154名中国人。 问题研讨(1)吉隆坡到北京约4500km,飞机速度900km/h,请问原计划几小时到达北京?(2)假设飞机一直在飞行,航行路程y(单位:km)与飞行时间x (单位:h)之间有什么关系?4500÷900=5(h)y=900x (0≤x≤5)(3)该航班由吉隆坡起飞2.5 h后,是否已经飞出马来西亚境外2 100 km的越南监测站?当x=2.5时,y=900×2.5=2250>2100,2.5 h后,已经飞出马来西亚境外2 100 km的越南监测站活动一:情境创设思考下列问题:
1. y=900x中,变量和常量分别是什么?其对应关系式是函数关系吗?谁是自变量,谁是函数?
2.自变量与常量按什么运算符号连接起来的?
3.(1)与(2)之间有何联系?(2)与(3)呢?活动二:问题再现下列问题中,变量之间的对应关系是函数关系吗?如果是,请写出函数解析式:
(1)圆的周长l 随半径r的变化而变化.
(2)铁的密度为7.8g/cm3,铁块的质量m(单位:g)随它的体积V(单位:cm3)的变化而变化.
活动二:问题再现 (3)每个练习本的厚度为0.5cm,
一些练习本摞在一起的总厚度h
(单位:cm)随练习本的本数n的
变化而变化.
(4)冷冻一个0°C的物体,使它每
分钟下降2°C,物体温度T(单位:°C)
随冷冻时间t(单位:min)的变化而变
化.
活动二:问题再现问题探究:在 、 、 和
中 :
(1)以上对应关系都是函数关系吗?其变量和常量分别是什么?进一步指出谁是自变量,谁是函数?
(2)认真观察自变量和常量运用什么运算符号连接起来的?这些变量可以取哪些值?
(3)这4个函数表达式与问题1的函数表达式 y=900x有何共同特征?请你用语言加以描述.活动三:形成概念1.如果我们把这个常数记为k,你能用数学式子表达吗?
y=kx
2.对这个常数k有何要求呢?为什么?
k≠0
3.请你尝试给这类特殊函数下个定义:
形如 y=kx(k≠0)的函数,叫做正比例函数,其中k叫比例系数
4.这个函数表达式在形式上一个单项式还是多项式?你能指出它的系数是什么?次数为多少?
形式上是一个一次单项式,单项式系数就是比例系数k活动三:形成概念5.正比例函数y=kx(常数k≠0)的自变量x的取值范围是什么?这与问题1和思考的(1)~(4)的函数自变量的取值范围有何不同?
一般情况下正比例函数自变量取值范围为一切实数,但在特殊情况下自变量取值范围会有所不同
6.如何理解y与x成正比例函数?反之,y=kx(k为常数, k≠0)表示什么意义?
y与x成正比例函数 y=kx(常数k≠0)活动三:形成概念7.在正比例函数y=kx(k为常数,k≠0)中关键是确定哪个量?比例系数k一经确定,正比例函数确定了吗?怎样确定k呢?
从函数关系看,关键是比例系数k,比例系数k一确定,正比例函数就确定了;只需知道两个变量x、y的一对对应值即可确定k值.
从方程角度看,如果三个量x、y、k中已知其中两个量,则一定可以求出第三个量. 活动四:辨析概念1.下列式子,哪些表示y是x的正比例函数?如果是,请你指出正比例系数k的值.
(1)y=-0.1x (2)
(3)y=2x2 (4)y2=4x
(5)y=-4x+3 (6)y=2(x-x2 )+2x2 是正比例函数,
正比例系数为-0.1是正比例函数,
正比例系数为0.5不是正比例函数不是正比例函数不是正比例函数是正比例函数,正比例系数为2判定一个函数是否是正比例函数,要从化简后来判断!活动四:辨析概念2.列式表示下列问题中y与x的函数关系,并指出哪些是正比例函数.
(1)正方形的边长为xcm,周长为ycm.
y=4x 是正比例函数
(2)某人一年内的月平均收入为x元,他这年(12个月)的总收入为y元.
y=12x 是正比例函数
(3)一个长方体的长为2cm,宽为1.5cm,高为xcm ,体积为ycm3.
y=3x 是正比例函数
活动五:判定正误下列说法正确的打“√”,错误的打“×”
(1)若y=kx,则y是x的正比例函数( )
(2)若y=2x2,则y是x的正比例函数( )
(3)若y=2(x-1)+2,则y是x的正比例函数( )
(4)若y=2(x-1) ,则y是x-1的正比例函数( )
××√在特定条件下自变量可能不单独就是x了,要注意自变量的变化√例:已知y与x成正比例,当x=4时,y=8,试求y与x的函数解析式解:设所求的正比例函数解析式为:y=kx把x=4,y=8代入上式得:8=4k 解得k=2∴y与x的函数解析式为:y=2x活动六:待定系数法求正比例函数解析式 正比例函数y=kx中,当x=2时,
y=10,则它的解析式是_________. 若一个正比例函数的比例系数是4,
则它的解析式是__________.y = 4xy = 5x必做题活动六:应用新知已知正比例函数y=2x中,
(1)若0< y <10,则x的取值范围为_________.
(2)若-6< x <10,则y的取值范围为_________.0< <10-6< <100
(2)当x=7时,求出y的值。(2)当x=7时,y=4×7=28活动六:应用新知
例3已知y与x-1成正比例,x=8时,y=6,写出y与x之间函数关系式,并分别求出x=4和x=-3时y的值。活动七: 变式应用 已知y与x+2 成正比例,当x=4时,y=12,那么当x=5时,y=______.解:∵ y与x+2 成正比例∴y=k(x+2)∵当x=4时,y=12∴12=k(4+2)解得:k=2∴y=2x+4∴当x=5时,y=1414活动七: 变式练习必做题 已知y=y1+y2,y1与x2成正比例,y2与x-2成正比例,当x=1时,y=0,当x=-3时,y=4,求x=3时,y的值。选做题活动八:课堂小结与作业布置你如何理解正比例函数的意义?能从哪几个方面去认识正比例函数?
1.从语言描述看:
函数关系式是常量与自变量的乘积.
2.从外形特征看:
(1)一般情况下y=kx(常数k≠0);
(2)在特定条件下自变量可能不单独是x了,要注意问题中自变量的变化.
3.从结果形式看:
函数表达式要化简后才能确认为正比例函数活动八:课堂小结与作业布置
4.从函数关系看:
比例系数k一确定,正比例函数就确定;必须知道两个变量x、y的一对对应值即可确定k.
5.从方程角度看:
如果三个量x、y、k中已知其中两个量,则一定可以求出第三个量.
6.求正比例函数解析式的两种方法:
(1)直接根据已知的比例系数求出解析式
(2)待定系数法 某学校准备添置一批篮球,已知所购篮球的总价y(元)与个数x(个)成正比例,当x=4(个)时,y=100(元)。
(1)求正比例函数关系式及自变量的取值范围;
(2)求当x=10(个)时,函数y的值;
(3)求当y=500(元)时,自变量x的值。解(1)设所求的正比例函数的解析式为y=kx,(2)当x=10(个)时,y=25x=25×10=250(元)。∵当x =4时,y =100,∴100=4k。解得 k= 25。∴所求正比例函数的解析式是y=25x。自变量x的取值范围是所有自然数。 1.下图表示江山到礼贤主要停靠站之间路程的千米数。一辆满载礼贤乘客的中巴车于上午8:00整从江山开往礼贤,已知中巴车行驶的路程S(千米)与时间t(分)成正比例(途中不停车),当t=4(分)时,S=2千米。问:(1)正比例函数的解析式;
(2)从8:30到8:40,该中巴车行驶在哪一段公路上;
(3)从何时到何时,该车行使在淤头至礼贤这段公路上。江山贺村淤头礼贤14千米6千米2千米 下图表示江山到礼贤主要停靠站之间路程的千米数。一辆满载礼贤乘客的中巴车于上午8:00整从江山开往礼贤,已知中巴车行驶的路程S(千米)与时间t(分)成正比例(途中不停车),当t=4(分)时,S=2千米。问:(1)正比例函数的解析式;
(2)从8:30到8:40,该中巴车行驶在哪一段公路上;
(3)从何时到何时,该车行使在淤头至礼贤这段公路上。江山贺村淤头礼贤14千米6千米2千米解(1)设所求的正比例函数的解析式为S=k t,(2)由已知得30≤t≤40,把t =4,S =2代入,得 2=4t。解得 k= 0.5 。所以,所求的正比例函数的解析式是S=0.5t。∴ 30≤2S≤40即15 ≤S≤20。由图可知中巴车行使在贺村至淤头公路上。(3)由已知得20≤S≤22,∴ 20≤0.5t≤22即40≤t≤44。所以从8:40至8:44,该车行使在淤头至礼贤公路上。
