人教版八年级数学下册课件:19.2.2 一次函数(共27张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:19.2.2 一次函数(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 16:28:06 | ||
图片预览







文档简介
课件27张PPT。19.2.2 一次函数——待定系数法学 习 目 标会用待定系数法确定一次函数解析式。
经历待定系数法应用过程,体验数形结合,具体感知数形结合思想在一次函数中的应用 。
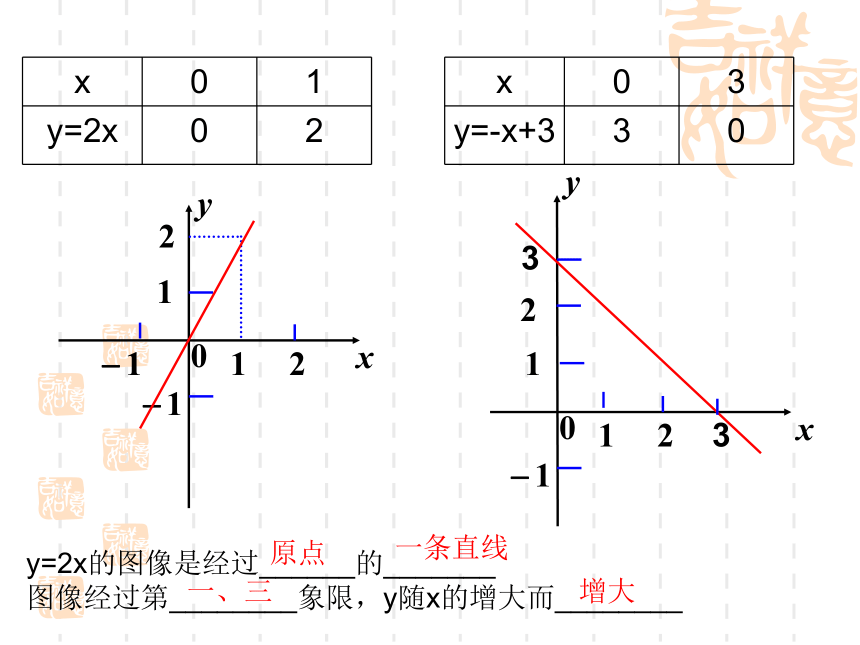
能把实际问题抽象为数学问题,也能把所学的知识运用于实际。一、创设情景,提出问题1、复习:2.反思:你能画出y=2x和y=-x+3的图象吗?你在作这两个函数图象时,分别描了几个点?
可以有不同取法吗?33y=2x的图像是经过______的_______
图像经过第________象限,y随x的增大而________一条直线原点一、三增大二、提出问题,形成思路 1.求下图中直线的函数表达式 小结:确定正比例函数的解析式需要 个条件
y=2x分析与思考:
图(1)是经过 的一条直线,
因此是 ,
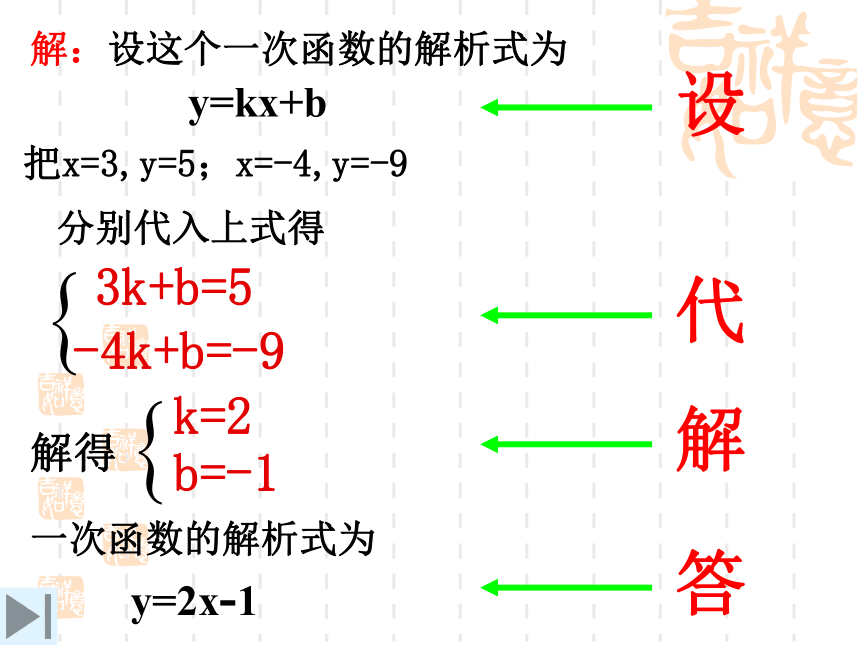
可设它的表达式为 ,将点 代入表达式得 从而确定该函数的表达式为 。(1,2)y=2xK=2y=kx正比例函数原点12猜想:确定一次函数的解析式需要 个条件. 例题:已知一次函数的图象经过点(3,5)与(-4,-9).求这个一次函数的解析式. 解:设这个一次函数的解析式为y=kx+b.∴这个一次函数的解析式为y=2x-1三、初步应用,感悟新知因为图象过(3,5)与(-4,-9)点,所以这两点的坐标必适合解析式把x=3,y=5;x=-4,y=-9分别代入上式得:
象这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法,叫做待定系数法.初步应用,感悟新知 你能归纳出待定系数法求函数解析式的基本步骤吗?设代解答思路:求一次函数的表达式
求k、b的值
列二元一次方程组
解方程组用待定系数法求一次函数解析式的基本步骤
找两点坐标 设 代 解 答 函数解析式y=kx+b满足条件的两定点一次函数的图象直线画出选取解出选取从数到形从形到数数学的基本思想方法:数形结合
整理归纳(一)根据已知条件,求函数解析式融会贯通——题型分类已知一次函数y=kx+b,当x=1时,y=1,当x=2时,y=3.求这个一次函数的解析式. 解:∴这个一次函数的解析式为y=2x-1∵当x=1时,y=1,当x=2时,y=3.(二)根据函数图象,求函数解析式
已知一次函数的图象如图所示,求出它的函数关系式解:设这个一次函数的解析式为y=kx+b(k≠0).∴这个一次函数的
解析式为y=-3x+3yx∵y=kx+b的图象过点(0,3)与(1,0).(三)求函数解析式的综合应用
如图,一次函数y=kx+b 的图象过点A(3,0).与y轴交于点B,若△AOB的面积为6,求这个一次函数的解析式 ∴OB=4, B点的坐标为(0,4),
则 y=kx+4解:∵y=kx+b的图象过点A(3,0).(四)与求函数解析式有关的实际应用题(2002佛山市题)某摩托车油箱最多可存油5升,行驶时油箱的余油量y(升)与行驶的路程x(千米)成一次函数的关系,其图象如图所示:
(1)求y与x的函数关系式;
(2)摩托车加满油后,最多能行驶多少千米 解:(1) 设y=kx+b(k≠0)当x=0时,y=5,∴ b=5.当x=60时,y=3,∴ 60k+5=3. ∴ k=-1/30(2) 把y=0代入函数关系式,得-1/30·x+5=0∴x=150故摩托车加满油后,最多能行驶150千米.“蛋”无虚发y的值为4, 求k的值.解:把x=5,y=4代入y=kx+2得:4=5k+2,解得 k=
3、若一次函数y=3x-b的图象经过点P(1,-1),则该函数图象必经过点( )
A(-1,1) B (2,2)
C(-2,2) D (2,一2) B4.若直线y=kx+b平行直线y=-3x+2,且过y轴上的(0,-5)点,则k= ,b= 。-3-5小明根据某个一次函数关系式填写了下表:其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是多少?解释你的理由。∴y=2x+2∴x=-1时y=0∵当x=0时,y=1,当x=1时,y=0.解:设这个一次函数的解析式为y=kx+b.延伸拓展 一次函数y=kx+b(k≠0)的自变量的取值范围是-3≤x≤6,相应函数值的范围是-5≤y≤-2,求这个函数的解析式.由于此题中没有明确k的正负,且一次函数y=kx+b(k≠0)只有在k>0时,y随x的增大而增大,在k<0时,y随x的增大而减小,故此题要分k>0和k<0两种情况进行讨论。六、课堂小结
待定系数法1、通过这节课的学习,你知道利用什么方法确 定正比例函数或一次函数的解析式吗?
2、你还记得利用待定系数法确定函数解析式的一般步骤吗?
一设二代三解四答3、体验了数形结合思想在解决函数问题作用!1.如图,折线ABC是在某市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图像。
① 根据图像,写出当x≥3时
该图像的函数关系式;BC② 某人乘坐2.5km,应付多少钱?每日一题③ 某人乘坐13km,应付多少钱?
④ 若某人付车费30.8元,出租车行驶了多少千米?解:① 设y=kx+b
把(3,7),(8,14)代入得:
3k+b=7
8k+b=14
解得:
∴(x≥3)② ∵2.5<3 由图可知
某人乘坐2.5km,应付7元钱③把x=13代入 ④ 把y=30.8代入
解得x=20
答:若某人付车费30.8元,出租车行驶了20千米。
y=21答:某人乘坐13km,应付21元钱
经历待定系数法应用过程,体验数形结合,具体感知数形结合思想在一次函数中的应用 。
能把实际问题抽象为数学问题,也能把所学的知识运用于实际。一、创设情景,提出问题1、复习:2.反思:你能画出y=2x和y=-x+3的图象吗?你在作这两个函数图象时,分别描了几个点?
可以有不同取法吗?33y=2x的图像是经过______的_______
图像经过第________象限,y随x的增大而________一条直线原点一、三增大二、提出问题,形成思路 1.求下图中直线的函数表达式 小结:确定正比例函数的解析式需要 个条件
y=2x分析与思考:
图(1)是经过 的一条直线,
因此是 ,
可设它的表达式为 ,将点 代入表达式得 从而确定该函数的表达式为 。(1,2)y=2xK=2y=kx正比例函数原点12猜想:确定一次函数的解析式需要 个条件. 例题:已知一次函数的图象经过点(3,5)与(-4,-9).求这个一次函数的解析式. 解:设这个一次函数的解析式为y=kx+b.∴这个一次函数的解析式为y=2x-1三、初步应用,感悟新知因为图象过(3,5)与(-4,-9)点,所以这两点的坐标必适合解析式把x=3,y=5;x=-4,y=-9分别代入上式得:
象这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法,叫做待定系数法.初步应用,感悟新知 你能归纳出待定系数法求函数解析式的基本步骤吗?设代解答思路:求一次函数的表达式
求k、b的值
列二元一次方程组
解方程组用待定系数法求一次函数解析式的基本步骤
找两点坐标 设 代 解 答 函数解析式y=kx+b满足条件的两定点一次函数的图象直线画出选取解出选取从数到形从形到数数学的基本思想方法:数形结合
整理归纳(一)根据已知条件,求函数解析式融会贯通——题型分类已知一次函数y=kx+b,当x=1时,y=1,当x=2时,y=3.求这个一次函数的解析式. 解:∴这个一次函数的解析式为y=2x-1∵当x=1时,y=1,当x=2时,y=3.(二)根据函数图象,求函数解析式
已知一次函数的图象如图所示,求出它的函数关系式解:设这个一次函数的解析式为y=kx+b(k≠0).∴这个一次函数的
解析式为y=-3x+3yx∵y=kx+b的图象过点(0,3)与(1,0).(三)求函数解析式的综合应用
如图,一次函数y=kx+b 的图象过点A(3,0).与y轴交于点B,若△AOB的面积为6,求这个一次函数的解析式 ∴OB=4, B点的坐标为(0,4),
则 y=kx+4解:∵y=kx+b的图象过点A(3,0).(四)与求函数解析式有关的实际应用题(2002佛山市题)某摩托车油箱最多可存油5升,行驶时油箱的余油量y(升)与行驶的路程x(千米)成一次函数的关系,其图象如图所示:
(1)求y与x的函数关系式;
(2)摩托车加满油后,最多能行驶多少千米 解:(1) 设y=kx+b(k≠0)当x=0时,y=5,∴ b=5.当x=60时,y=3,∴ 60k+5=3. ∴ k=-1/30(2) 把y=0代入函数关系式,得-1/30·x+5=0∴x=150故摩托车加满油后,最多能行驶150千米.“蛋”无虚发y的值为4, 求k的值.解:把x=5,y=4代入y=kx+2得:4=5k+2,解得 k=
3、若一次函数y=3x-b的图象经过点P(1,-1),则该函数图象必经过点( )
A(-1,1) B (2,2)
C(-2,2) D (2,一2) B4.若直线y=kx+b平行直线y=-3x+2,且过y轴上的(0,-5)点,则k= ,b= 。-3-5小明根据某个一次函数关系式填写了下表:其中有一格不慎被墨汁遮住了,想想看,该空格里原来填的数是多少?解释你的理由。∴y=2x+2∴x=-1时y=0∵当x=0时,y=1,当x=1时,y=0.解:设这个一次函数的解析式为y=kx+b.延伸拓展 一次函数y=kx+b(k≠0)的自变量的取值范围是-3≤x≤6,相应函数值的范围是-5≤y≤-2,求这个函数的解析式.由于此题中没有明确k的正负,且一次函数y=kx+b(k≠0)只有在k>0时,y随x的增大而增大,在k<0时,y随x的增大而减小,故此题要分k>0和k<0两种情况进行讨论。六、课堂小结
待定系数法1、通过这节课的学习,你知道利用什么方法确 定正比例函数或一次函数的解析式吗?
2、你还记得利用待定系数法确定函数解析式的一般步骤吗?
一设二代三解四答3、体验了数形结合思想在解决函数问题作用!1.如图,折线ABC是在某市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图像。
① 根据图像,写出当x≥3时
该图像的函数关系式;BC② 某人乘坐2.5km,应付多少钱?每日一题③ 某人乘坐13km,应付多少钱?
④ 若某人付车费30.8元,出租车行驶了多少千米?解:① 设y=kx+b
把(3,7),(8,14)代入得:
3k+b=7
8k+b=14
解得:
∴(x≥3)② ∵2.5<3 由图可知
某人乘坐2.5km,应付7元钱③把x=13代入 ④ 把y=30.8代入
解得x=20
答:若某人付车费30.8元,出租车行驶了20千米。
y=21答:某人乘坐13km,应付21元钱
