人教版数学七年级下册:5.3.3 平行线的判定与性质 习题课件(共17张PPT)
文档属性
| 名称 | 人教版数学七年级下册:5.3.3 平行线的判定与性质 习题课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 131.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 10:38:29 | ||
图片预览





文档简介
课件17张PPT。
人教版 七年级数学下册
第5章 相交线与平行线
5.3 平行线的判定与性质 习题课
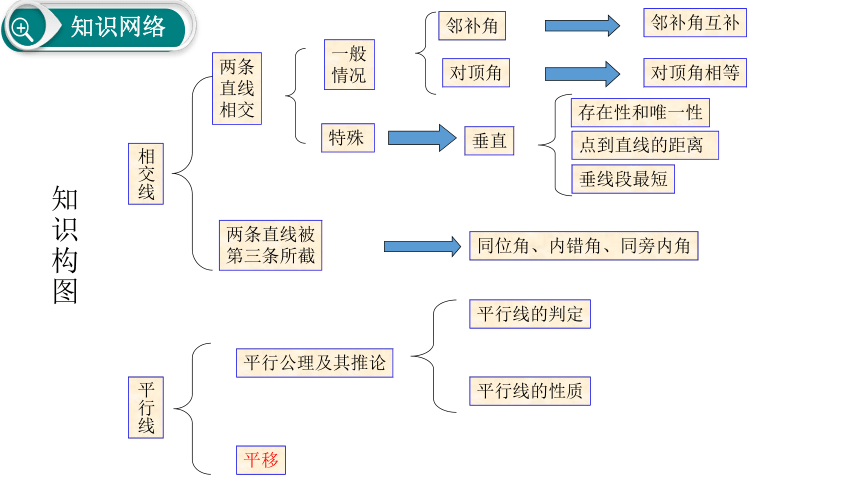
相交线两条
直线
相交两条直线被
第三条所截一般情况邻补角对顶角邻补角互补对顶角相等特殊垂直存在性和唯一性垂线段最短点到直线的距离同位角、内错角、同旁内角平行线平行公理及其推论平行线的判定平行线的性质平移知识构图【例1】如图,AB⊥CD于点O,直线EF过O点,∠AOE=65°,
求∠DOF的度数.解:∵AB⊥CD,
∴∠AOC=90°.
∵∠AOE=65°,
∴∠COE=25°专题一 相交线又∵∠COE=∠DOF
(对顶角相等)
∴∠DOF=25°.【迁移应用1】如图,AB,CD相交于点O,∠AOC=70°,EF平分∠COB,求∠COE的度数.答案:∠COE=125°.【归纳拓展】两条直线相交包括垂直和斜交两种情形.相交时形成了两对对顶角和四对邻补角.其中垂直是相交的特殊情况,它将一个周角分成了四个直角.②∠AOC=70°∠AOE=55°∠COF+∠FOB=110°∠FOB=55°【例2】如图,AD为 △ABC 的高,能表示点到直线(线段)的距离的线段有( )
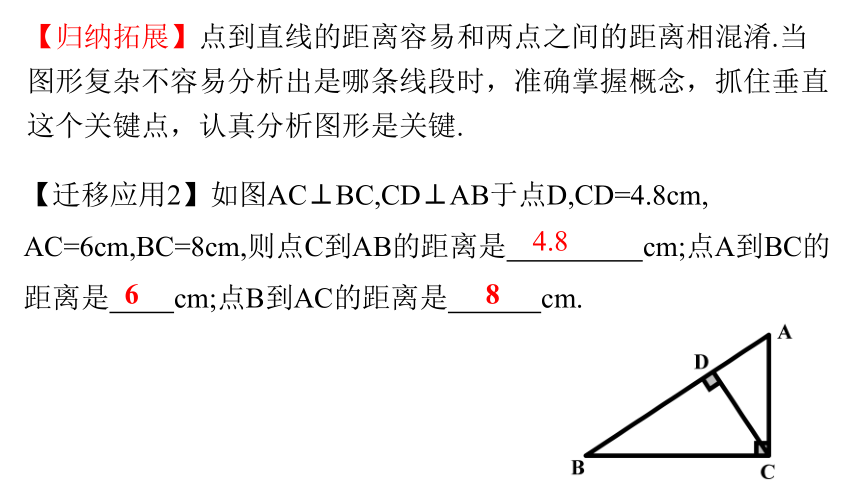
A.2条 B.3条 C.4条 D.5条专题二 点到直线的距离B 点拨:从图中可以看到共有三条,A到BC的垂线段AD,B到AD的垂线段BD,C到AD的垂线段CD. √【迁移应用2】如图AC⊥BC,CD⊥AB于点D,CD=4.8cm,
AC=6cm,BC=8cm,则点C到AB的距离是 cm;点A到BC的距离是 cm;点B到AC的距离是 cm.【归纳拓展】点到直线的距离容易和两点之间的距离相混淆.当图形复杂不容易分析出是哪条线段时,准确掌握概念,抓住垂直这个关键点,认真分析图形是关键.4.868【例3】(1)如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4度数.解:∵∠1=∠2 = 72°
∴a // b (内错角相等,两直线平行)
∴∠3+∠4=180°
(两直线平行,同旁内角互补)
∵∠3=60°
∴∠4=120°专题三 平行线的性质和判定证明: ∵∠DAC= ∠ACB (已知)
∴ AD// BC(内错角相等,两直线平行)
∵ ∠D+∠DFE=180°(已知)
∴ AD// EF(同旁内角互补,两直线平行)
∴ EF// BC(平行于同一条直线的两条直线互相平行)
(2)已知∠DAC=∠ACB,∠D+∠DFE=180°,求证:EF//BC.ABCDEF答案:100°.【归纳拓展】平行线的性质和判定经常结合使用,由角之间的关系得出直线平行,进而再得出其他角之间的关系,或是由直线平行得到角之间的关系,进而再由角的关系得出其他直线平行.思路点拨: 折 叠∠1=∠2∠1=∠3AD//BC 解:设∠1的度数为x°,则∠2的度数为x°,
则∠3的度数为8x°,根据题意可得
x°+x°+8x°=180°,解得x=18.
即∠1=∠2=18°,
而∠4=∠1+∠2(对顶角相等).
故∠4=36°.
答:∠4为36°专题四 相交线中的方程思想【迁移应用4】如图所示,直线AB与CD相交于点O,
∠AOC : ∠AOD = 2 : 3,求∠BOD 的度数.答案:72° 【归纳拓展】利用方程解决问题,是几何与代数知识相结合的一种体现,它可以使解题思路清晰,过程简便.在有关线段或角的求值问题中它的应用非常广泛.思路点拨:用方程思想.设未知数, 找等量关系,列方程解决。本节课所复习的主要内容:1、相交线
2、点到直线的距离
3、平行线的性质和判定
4、相交线中的方程思想若AB∥CD, 则∠ =∠ . 课后训练1.如图, 若∠3=∠4,则 ∥ ;AD1⌒⌒⌒⌒CD1432BC22.如图,∠D=70°,∠C= 110°,∠1=69°,则∠B= ·BACED⌒169°AB3. 如图,直线AB、CD相交于O,∠AOC=80°,∠1=30°;
求∠2的度数.ACDE12))O答案:50°B4. 已知:如图AB∥CD,试探究∠BED与∠B,∠D的关系?ABCDE图甲图乙答案:∠BED+∠B+∠D=360°∠BED=∠B+∠D提示:过点E分别作AB的平行线,把∠BED一分为二.5.如图1,已知 AB∥CD, ∠1=30°, ∠2=90°,则∠3= °6.如图2,若AE∥CD, ∠EBF=135°,∠BFD=60°,∠D=( )
A.75° B.45° C.30° D.15°图1图260D课后训练分层作业必做题:1.如图,三条直线AB,CD,EF相交于O,且CD⊥EF,∠AOE=70o,若OG平分∠BOF.求∠DOG的度数.选做题:已知 EF⊥AB,CD⊥AB,∠EFB=∠GDC,求证:∠AGD=∠ACB.必做题:2.已知,
如图OA⊥OC,OB⊥OD,
∠AOB:∠BOC=32:13,
求∠COD的度数.
人教版 七年级数学下册
第5章 相交线与平行线
5.3 平行线的判定与性质 习题课
相交线两条
直线
相交两条直线被
第三条所截一般情况邻补角对顶角邻补角互补对顶角相等特殊垂直存在性和唯一性垂线段最短点到直线的距离同位角、内错角、同旁内角平行线平行公理及其推论平行线的判定平行线的性质平移知识构图【例1】如图,AB⊥CD于点O,直线EF过O点,∠AOE=65°,
求∠DOF的度数.解:∵AB⊥CD,
∴∠AOC=90°.
∵∠AOE=65°,
∴∠COE=25°专题一 相交线又∵∠COE=∠DOF
(对顶角相等)
∴∠DOF=25°.【迁移应用1】如图,AB,CD相交于点O,∠AOC=70°,EF平分∠COB,求∠COE的度数.答案:∠COE=125°.【归纳拓展】两条直线相交包括垂直和斜交两种情形.相交时形成了两对对顶角和四对邻补角.其中垂直是相交的特殊情况,它将一个周角分成了四个直角.②∠AOC=70°∠AOE=55°∠COF+∠FOB=110°∠FOB=55°【例2】如图,AD为 △ABC 的高,能表示点到直线(线段)的距离的线段有( )
A.2条 B.3条 C.4条 D.5条专题二 点到直线的距离B 点拨:从图中可以看到共有三条,A到BC的垂线段AD,B到AD的垂线段BD,C到AD的垂线段CD. √【迁移应用2】如图AC⊥BC,CD⊥AB于点D,CD=4.8cm,
AC=6cm,BC=8cm,则点C到AB的距离是 cm;点A到BC的距离是 cm;点B到AC的距离是 cm.【归纳拓展】点到直线的距离容易和两点之间的距离相混淆.当图形复杂不容易分析出是哪条线段时,准确掌握概念,抓住垂直这个关键点,认真分析图形是关键.4.868【例3】(1)如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4度数.解:∵∠1=∠2 = 72°
∴a // b (内错角相等,两直线平行)
∴∠3+∠4=180°
(两直线平行,同旁内角互补)
∵∠3=60°
∴∠4=120°专题三 平行线的性质和判定证明: ∵∠DAC= ∠ACB (已知)
∴ AD// BC(内错角相等,两直线平行)
∵ ∠D+∠DFE=180°(已知)
∴ AD// EF(同旁内角互补,两直线平行)
∴ EF// BC(平行于同一条直线的两条直线互相平行)
(2)已知∠DAC=∠ACB,∠D+∠DFE=180°,求证:EF//BC.ABCDEF答案:100°.【归纳拓展】平行线的性质和判定经常结合使用,由角之间的关系得出直线平行,进而再得出其他角之间的关系,或是由直线平行得到角之间的关系,进而再由角的关系得出其他直线平行.思路点拨: 折 叠∠1=∠2∠1=∠3AD//BC 解:设∠1的度数为x°,则∠2的度数为x°,
则∠3的度数为8x°,根据题意可得
x°+x°+8x°=180°,解得x=18.
即∠1=∠2=18°,
而∠4=∠1+∠2(对顶角相等).
故∠4=36°.
答:∠4为36°专题四 相交线中的方程思想【迁移应用4】如图所示,直线AB与CD相交于点O,
∠AOC : ∠AOD = 2 : 3,求∠BOD 的度数.答案:72° 【归纳拓展】利用方程解决问题,是几何与代数知识相结合的一种体现,它可以使解题思路清晰,过程简便.在有关线段或角的求值问题中它的应用非常广泛.思路点拨:用方程思想.设未知数, 找等量关系,列方程解决。本节课所复习的主要内容:1、相交线
2、点到直线的距离
3、平行线的性质和判定
4、相交线中的方程思想若AB∥CD, 则∠ =∠ . 课后训练1.如图, 若∠3=∠4,则 ∥ ;AD1⌒⌒⌒⌒CD1432BC22.如图,∠D=70°,∠C= 110°,∠1=69°,则∠B= ·BACED⌒169°AB3. 如图,直线AB、CD相交于O,∠AOC=80°,∠1=30°;
求∠2的度数.ACDE12))O答案:50°B4. 已知:如图AB∥CD,试探究∠BED与∠B,∠D的关系?ABCDE图甲图乙答案:∠BED+∠B+∠D=360°∠BED=∠B+∠D提示:过点E分别作AB的平行线,把∠BED一分为二.5.如图1,已知 AB∥CD, ∠1=30°, ∠2=90°,则∠3= °6.如图2,若AE∥CD, ∠EBF=135°,∠BFD=60°,∠D=( )
A.75° B.45° C.30° D.15°图1图260D课后训练分层作业必做题:1.如图,三条直线AB,CD,EF相交于O,且CD⊥EF,∠AOE=70o,若OG平分∠BOF.求∠DOG的度数.选做题:已知 EF⊥AB,CD⊥AB,∠EFB=∠GDC,求证:∠AGD=∠ACB.必做题:2.已知,
如图OA⊥OC,OB⊥OD,
∠AOB:∠BOC=32:13,
求∠COD的度数.
