人教版八年级数学下册17.1 勾股定理 课件(共29张ppt)
文档属性
| 名称 | 人教版八年级数学下册17.1 勾股定理 课件(共29张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 16:45:59 | ||
图片预览



文档简介
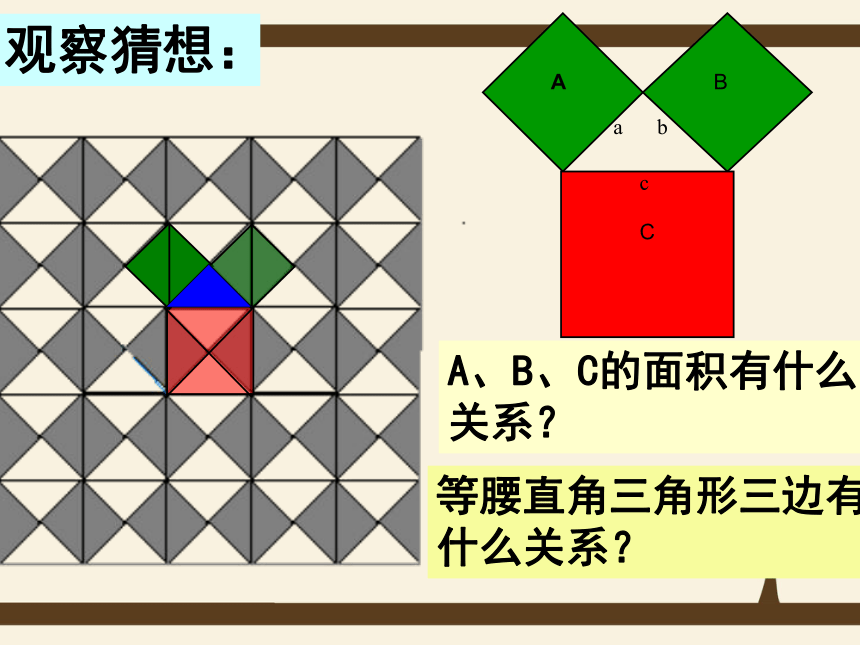
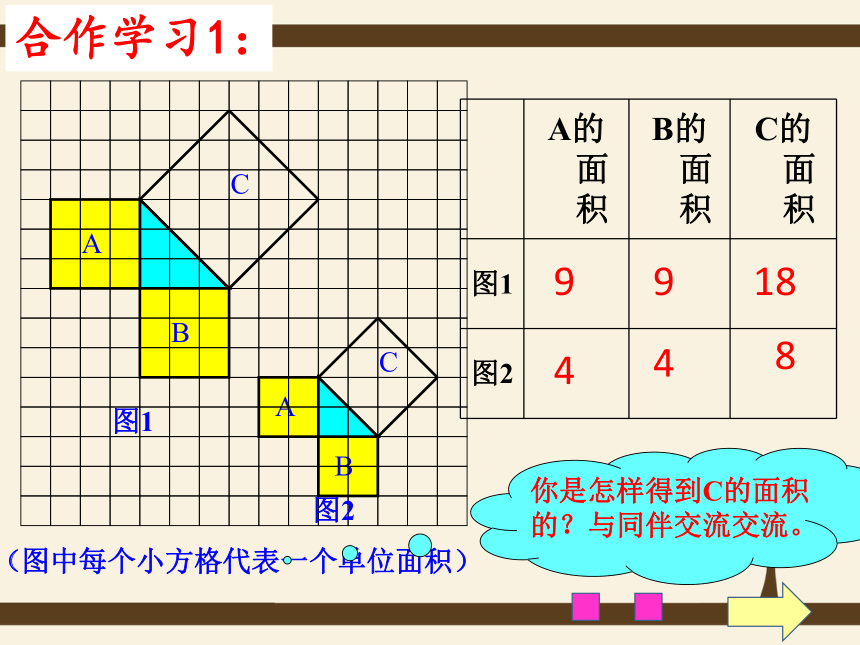
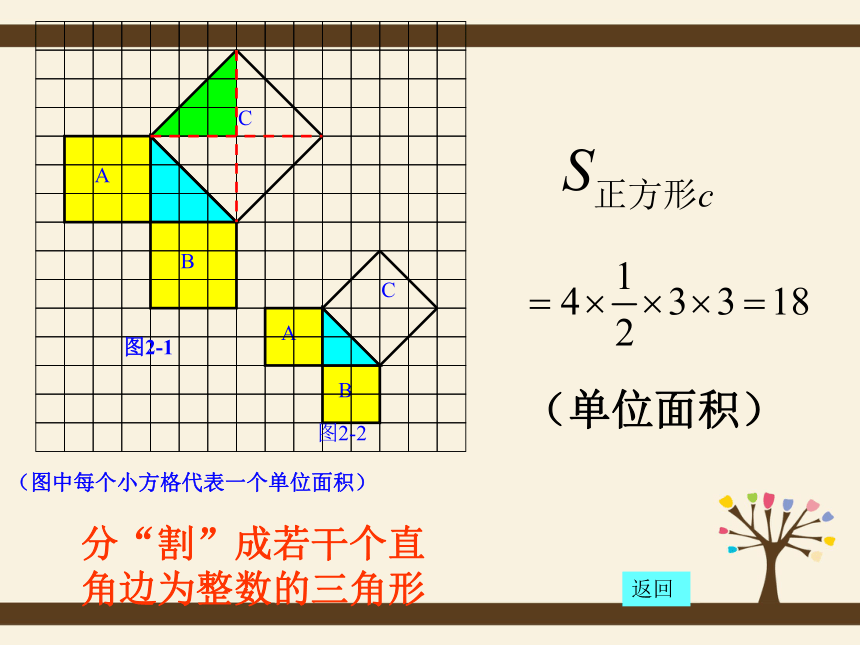
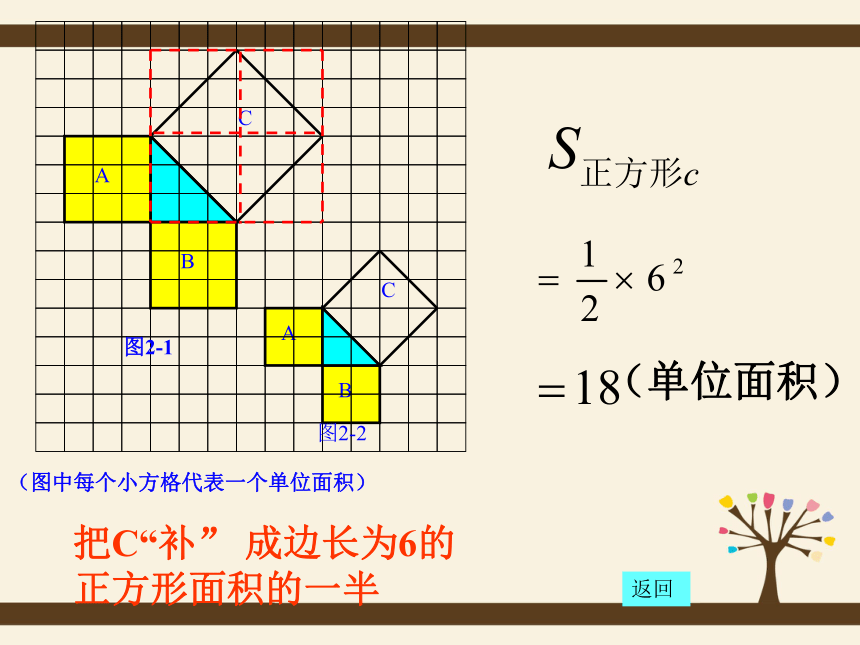
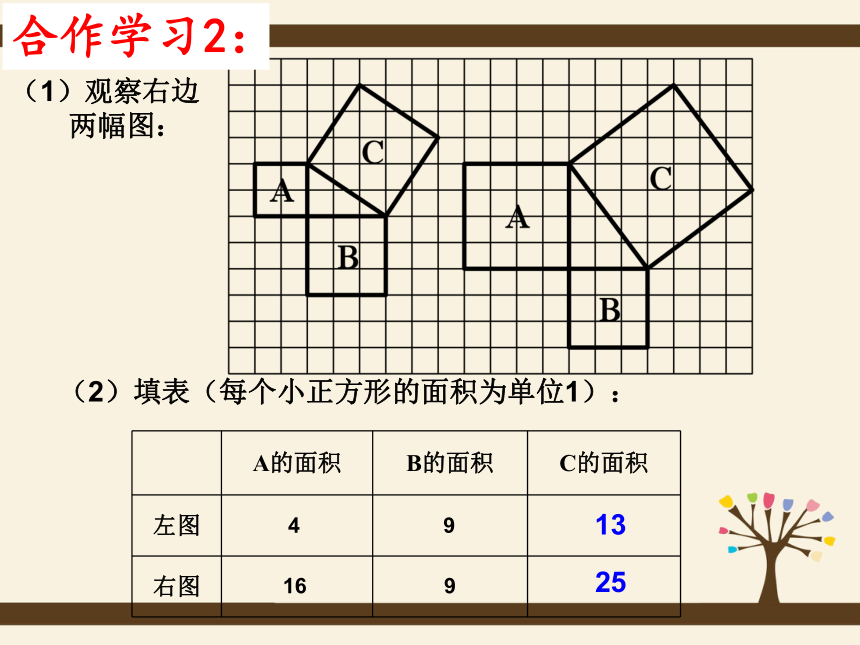
课件29张PPT。勾股定理赵爽弦图17.1 勾股定理2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系。同学们,我们也来观察下面的图案,看看你能发现什么?观察探讨:2500多年前,古希腊著名的哲学家、数学家、天文学家毕达哥拉斯观察猜想:A、B、C的面积有什么关系?等腰直角三角形三边有什么关系?合作学习1:9189448分“割”成若干个直角边为整数的三角形(单位面积)返回(单位面积)把C“补” 成边长为6的正方形面积的一半返回(1)观察右边
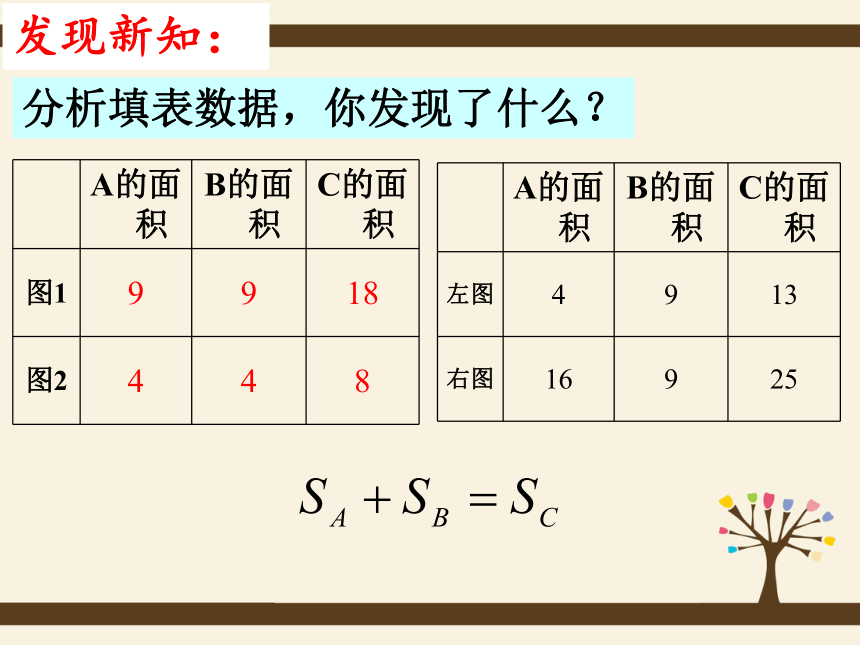
两幅图: (2)填表(每个小正方形的面积为单位1):4 916 91325合作学习2:分析填表数据,你发现了什么? 发现新知: 结论: 以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.得出结论:图乙SA+SB=SCSA+SB=SC图甲abcabc3.猜想直角三角形三边a、b、c 之间的关系?a2 +b2 =c2┏a2+b2=c2acb 命题: 如果直角三角形两直角边长分别为a和b,斜边长为c,则: 1、拿出准备好的四个全等的直角三角形
(设直角三角形的两条直角边分别为a,b,
斜边c); 2、你能用这四个直角三角形拼成一个正方形 吗?拼一拼试试看验证发现:∵ c2==b2-2ab+a2+ 2ab =a2+b2∴a2+b2=c2大正方形的面积可以表示为 ;
也可以表示为c2 该图2002年8月在北京召开的国际数学家大会的会标示意图,取材于我国古代数学著作《周髀算经》。操作论证:“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,是我国古代数学的骄傲。因此,当 2002年第24届国际数学家大会在北京召开时, “赵爽弦图”被选作大会会徽。勾股定理(毕达哥拉斯定理) 如果直角三角形两直角边分别为a, b,斜边为c,那么 即直角三角形两直角边的平方和等于
斜边的平方.ac勾弦b股得出概念 例、如图,要登上8米高的建筑物BC,为了安全需要,需使梯子底端离建筑物距离AB为6米,问至少需要多长的梯子?解:∵AB⊥BC
∴∠ABC = 90°
根据勾股定理得:
AC2 = AB2 +BC 2
= 62 + 82
= 36+64
= 100
即:AC = 10
答:梯子至少长10米。例题讲解: 如图,要登上8米高的建筑物BC,梯子AC的长为10米,为了安全需要,问至少需使梯子底端离建筑物距离AB为多长? ( ) 变式练习:10mA、5米
B、6米
C、7米
D、8米 B时间: 3分钟1:图中已知数据表示面积,求表示边的未知数x、的值.2:已知S1=1,S2=3, S3=2,S4=4 , 求S5 、S6 、S7的值.3、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为 ( )A.50米 B.120米 C.100米 D.130米A 4、如图,学校有一块长方形花园,有极少数人为了避开拐角走“捷径”,在花园内走出了一条“路”,仅仅少走了____步路, 却踩伤了花草。 (假设1米为2步)
44m“路”453mD探索思考:如图:一旗杆长18米,在某处断裂,旗杆顶部落在离旗杆底部12米处,则旗杆断裂处距地面是( ) A. 10米 B. 9米 C. 5米 D. 8米课堂小结⒈ 勾股定理揭示了直角三角形三边之间的数量关系。⒉勾股定理: 直角三角形两直角边a、b的平方和,等于斜边c的平方。
a2+b2 =c2⒊勾股定理的主要作用是:在直角三角形中,已知任意两边求第三边的长。
1、小练习册
2、预习25页
3、教材第28页习题17.1第1、2、3题
作业:谢谢指导!
两幅图: (2)填表(每个小正方形的面积为单位1):4 916 91325合作学习2:分析填表数据,你发现了什么? 发现新知: 结论: 以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.得出结论:图乙SA+SB=SCSA+SB=SC图甲abcabc3.猜想直角三角形三边a、b、c 之间的关系?a2 +b2 =c2┏a2+b2=c2acb 命题: 如果直角三角形两直角边长分别为a和b,斜边长为c,则: 1、拿出准备好的四个全等的直角三角形
(设直角三角形的两条直角边分别为a,b,
斜边c); 2、你能用这四个直角三角形拼成一个正方形 吗?拼一拼试试看验证发现:∵ c2==b2-2ab+a2+ 2ab =a2+b2∴a2+b2=c2大正方形的面积可以表示为 ;
也可以表示为c2 该图2002年8月在北京召开的国际数学家大会的会标示意图,取材于我国古代数学著作《周髀算经》。操作论证:“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,是我国古代数学的骄傲。因此,当 2002年第24届国际数学家大会在北京召开时, “赵爽弦图”被选作大会会徽。勾股定理(毕达哥拉斯定理) 如果直角三角形两直角边分别为a, b,斜边为c,那么 即直角三角形两直角边的平方和等于
斜边的平方.ac勾弦b股得出概念 例、如图,要登上8米高的建筑物BC,为了安全需要,需使梯子底端离建筑物距离AB为6米,问至少需要多长的梯子?解:∵AB⊥BC
∴∠ABC = 90°
根据勾股定理得:
AC2 = AB2 +BC 2
= 62 + 82
= 36+64
= 100
即:AC = 10
答:梯子至少长10米。例题讲解: 如图,要登上8米高的建筑物BC,梯子AC的长为10米,为了安全需要,问至少需使梯子底端离建筑物距离AB为多长? ( ) 变式练习:10mA、5米
B、6米
C、7米
D、8米 B时间: 3分钟1:图中已知数据表示面积,求表示边的未知数x、的值.2:已知S1=1,S2=3, S3=2,S4=4 , 求S5 、S6 、S7的值.3、湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为 ( )A.50米 B.120米 C.100米 D.130米A 4、如图,学校有一块长方形花园,有极少数人为了避开拐角走“捷径”,在花园内走出了一条“路”,仅仅少走了____步路, 却踩伤了花草。 (假设1米为2步)
44m“路”453mD探索思考:如图:一旗杆长18米,在某处断裂,旗杆顶部落在离旗杆底部12米处,则旗杆断裂处距地面是( ) A. 10米 B. 9米 C. 5米 D. 8米课堂小结⒈ 勾股定理揭示了直角三角形三边之间的数量关系。⒉勾股定理: 直角三角形两直角边a、b的平方和,等于斜边c的平方。
a2+b2 =c2⒊勾股定理的主要作用是:在直角三角形中,已知任意两边求第三边的长。
1、小练习册
2、预习25页
3、教材第28页习题17.1第1、2、3题
作业:谢谢指导!
