人教版八年级数学下册课件 17.1 勾股定理——数形结合之美(共18张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件 17.1 勾股定理——数形结合之美(共18张PPT) | 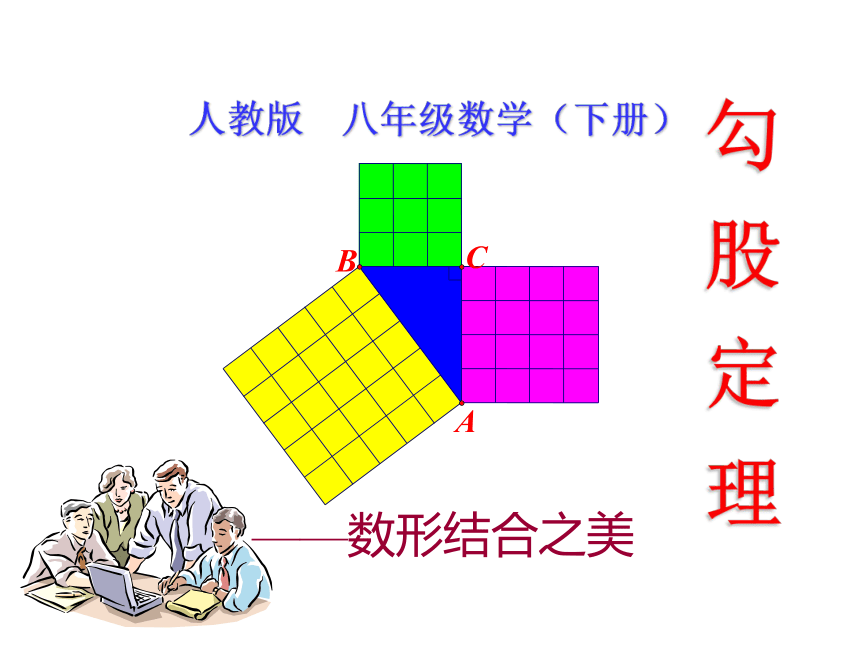 | |
| 格式 | zip | ||
| 文件大小 | 792.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 17:07:13 | ||
图片预览


文档简介
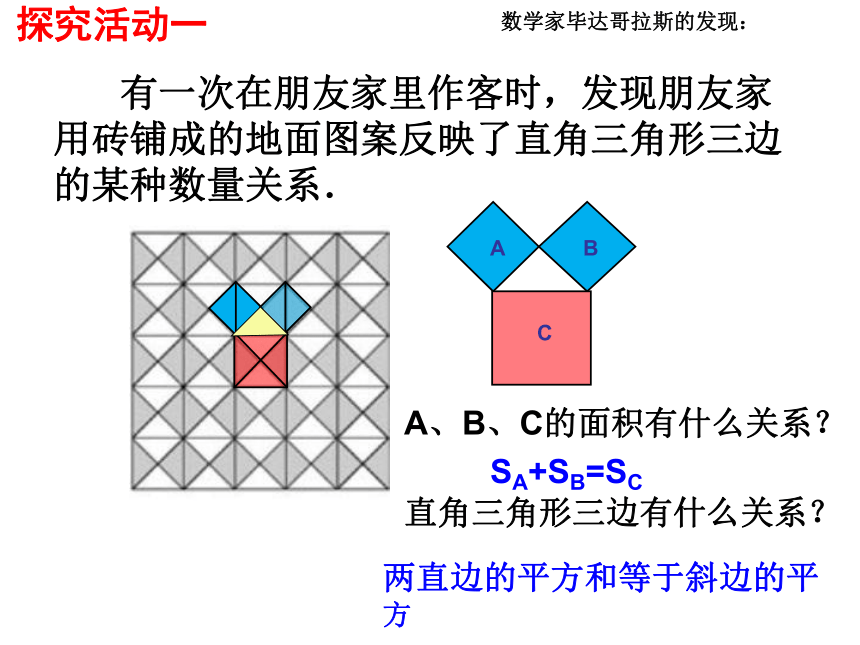
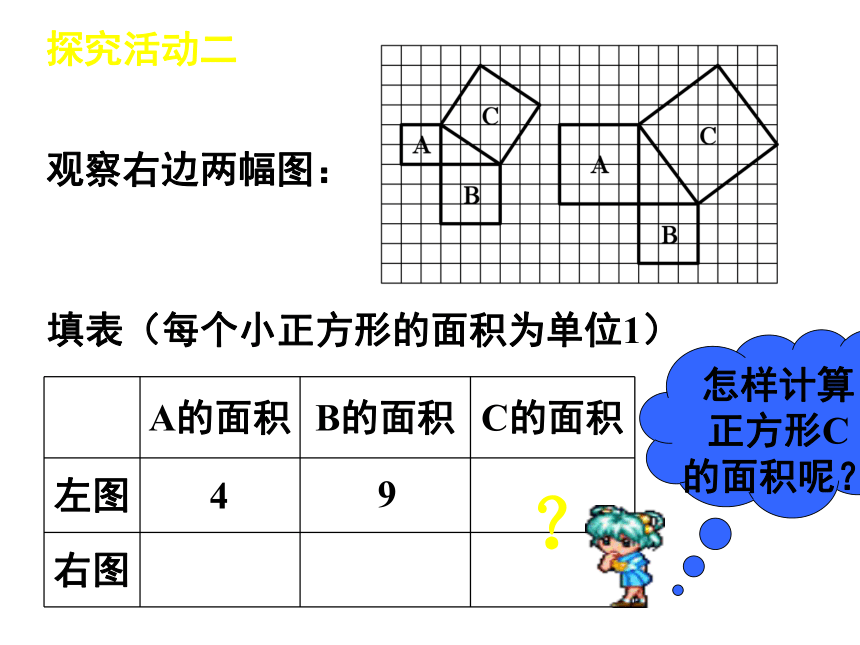
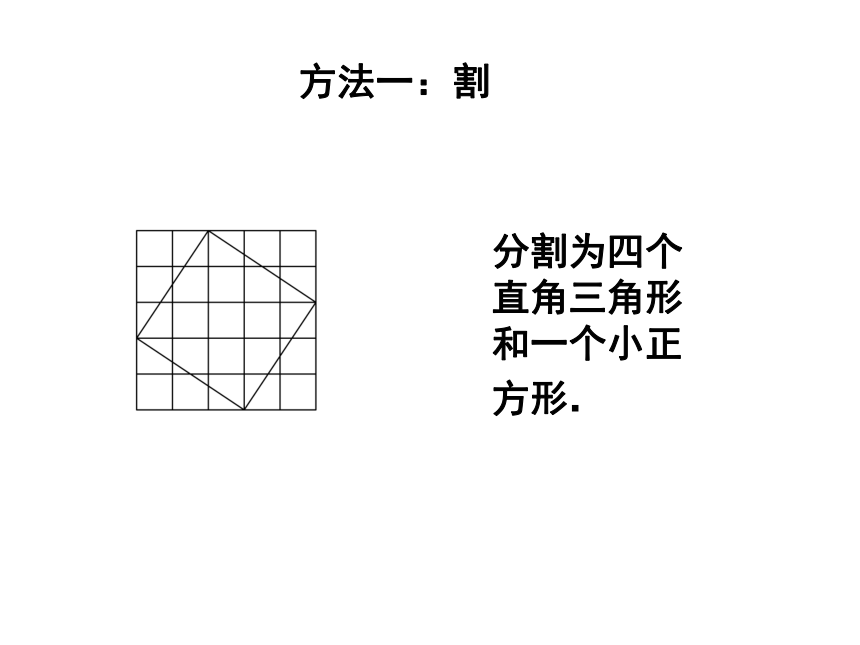
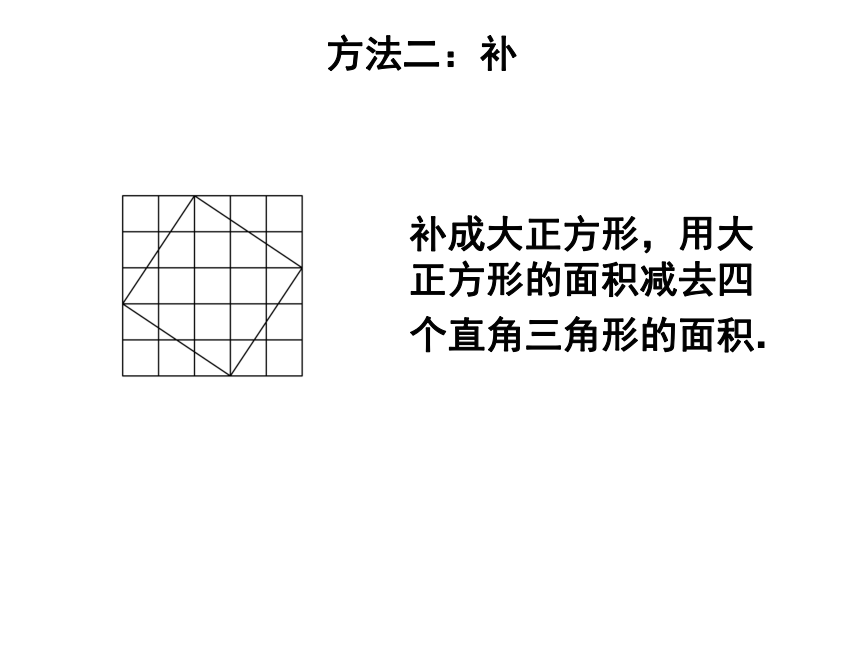
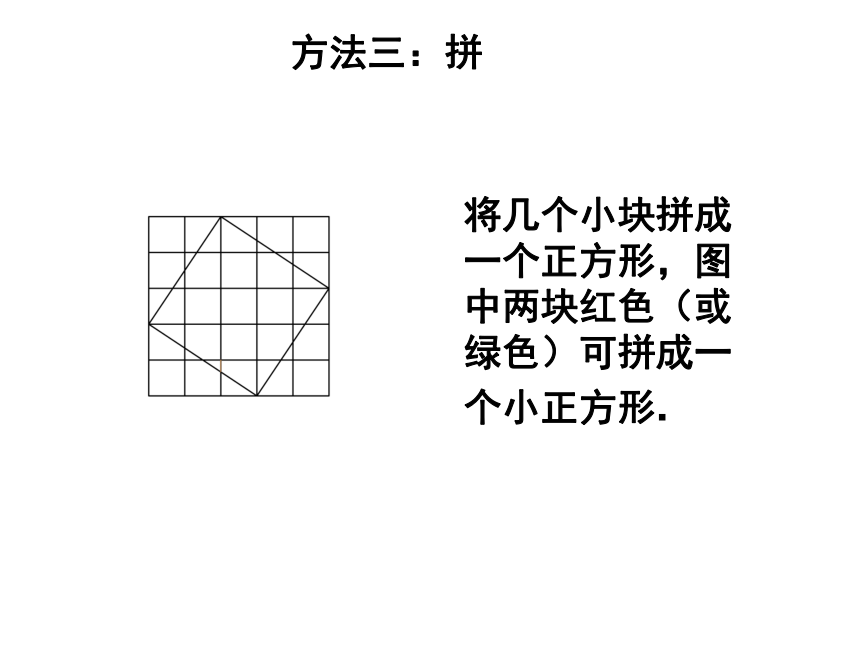
课件18张PPT。勾 股 定 理——数形结合之美人教版 八年级数学(下册) 数学家毕达哥拉斯的发现:A、B、C的面积有什么关系?直角三角形三边有什么关系?SA+SB=SC两直边的平方和等于斜边的平方 有一次在朋友家里作客时,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.探究活动一探究活动二观察右边两幅图: 填表(每个小正方形的面积为单位1)4 ?怎样计算正方形C的面积呢?9 方法一:割分割为四个直角三角形和一个小正方形.方法二:补补成大正方形,用大正方形的面积减去四个直角三角形的面积.方法三:拼将几个小块拼成一个正方形,图中两块红色(或绿色)可拼成一个小正方形.结论:
(1) 以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.结论:(2)若直角三角形的两直角边用a,b 表示,斜边用c表示,你能用自己的语言表述你所发现的结论吗?拼一拼现有四个全等的三角形,两直角边分别为a,b,斜边为c,请同学们动手拼一拼:
1.请用尽可能多的方法拼成一个正方形;
2.请用不同的方法表示你所拼出的大正方形的面积。∵S大正方形=c2
S大正方形=4S直角三角形+ S小正方形
=4· ab+(b-a)2
=2ab+b2-2ab+a2
=a2+b2活动三:验证a、b、c 之间的关系?证法一∴a2+b2=c2用拼图法证明(a+b)2=a2 + b2 + 2ab = c2+2ab可得: a2 + b2 =c2证法二用拼图法证明勾股定理 如果直角三角形两直角边分别为a,b,斜边为c,那么ac勾弦b股归纳定理:强调:勾股定理反映了直角三角形的三边关系。
1、求下列图中字母所表示的正方形的面积=625=144 例1:在Rt△ABC中,∠C=90°,
(1) 已知:AC=6,BC=8,求AB;
(2) 已知:AB=13,AC=5,求BC;例题分析在直角三角形中,已知两边,可求第三边;方法小结变式 :已知:Rt△ABC中,AB=4,AC=3,则BC的长为 .1、已知:Rt△ABC中, ∠A =90° AB=4,AC=3,则BC的长为5 漂亮的勾股树收获无处不在我知道了… …我感受了… …我探索了… …勾
股
定
理数形c2=a2+b2 2、查阅有关勾股定理的历史资料,及证明方法,与同学交流。 作业家庭作业:
1、 课本56页,第1、2题;
(1) 以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.结论:(2)若直角三角形的两直角边用a,b 表示,斜边用c表示,你能用自己的语言表述你所发现的结论吗?拼一拼现有四个全等的三角形,两直角边分别为a,b,斜边为c,请同学们动手拼一拼:
1.请用尽可能多的方法拼成一个正方形;
2.请用不同的方法表示你所拼出的大正方形的面积。∵S大正方形=c2
S大正方形=4S直角三角形+ S小正方形
=4· ab+(b-a)2
=2ab+b2-2ab+a2
=a2+b2活动三:验证a、b、c 之间的关系?证法一∴a2+b2=c2用拼图法证明(a+b)2=a2 + b2 + 2ab = c2+2ab可得: a2 + b2 =c2证法二用拼图法证明勾股定理 如果直角三角形两直角边分别为a,b,斜边为c,那么ac勾弦b股归纳定理:强调:勾股定理反映了直角三角形的三边关系。
1、求下列图中字母所表示的正方形的面积=625=144 例1:在Rt△ABC中,∠C=90°,
(1) 已知:AC=6,BC=8,求AB;
(2) 已知:AB=13,AC=5,求BC;例题分析在直角三角形中,已知两边,可求第三边;方法小结变式 :已知:Rt△ABC中,AB=4,AC=3,则BC的长为 .1、已知:Rt△ABC中, ∠A =90° AB=4,AC=3,则BC的长为5 漂亮的勾股树收获无处不在我知道了… …我感受了… …我探索了… …勾
股
定
理数形c2=a2+b2 2、查阅有关勾股定理的历史资料,及证明方法,与同学交流。 作业家庭作业:
1、 课本56页,第1、2题;
