人教版八年级数学下册课件:17.1 勾股定理(共17张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:17.1 勾股定理(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 395.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 17:08:30 | ||
图片预览


文档简介
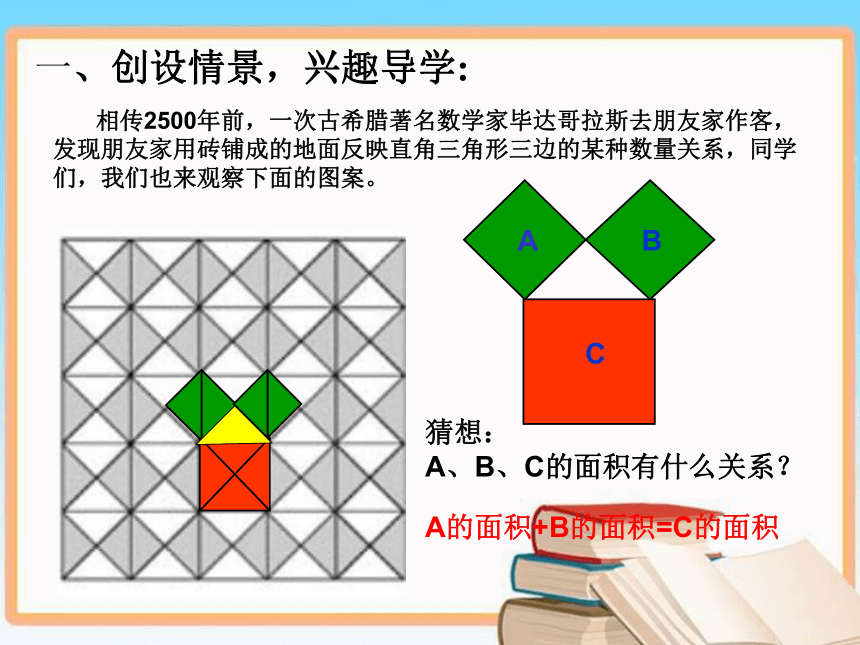
课件17张PPT。人教版八年级(下)第十七章勾股定理 相传2500年前,一次古希腊著名数学家毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案。猜想:
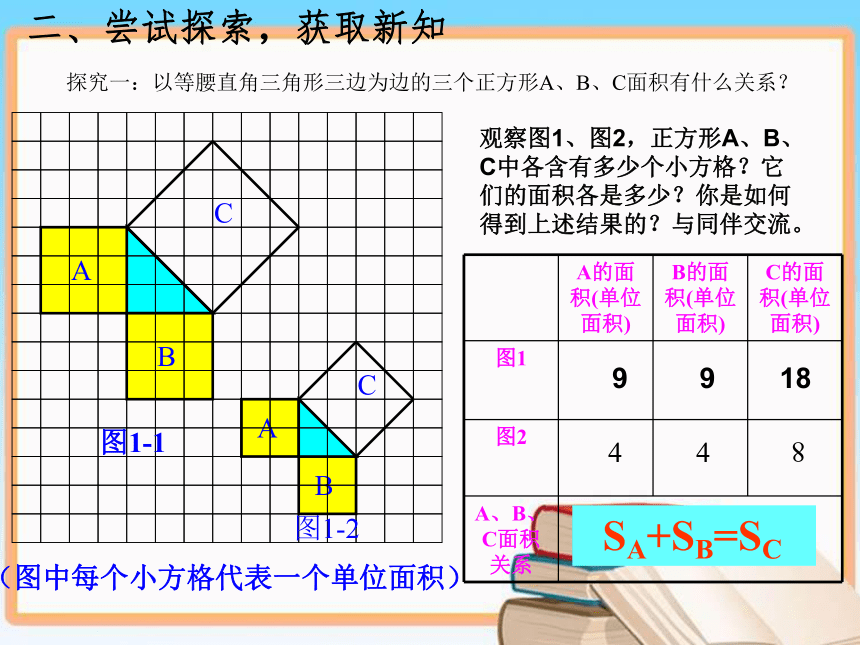
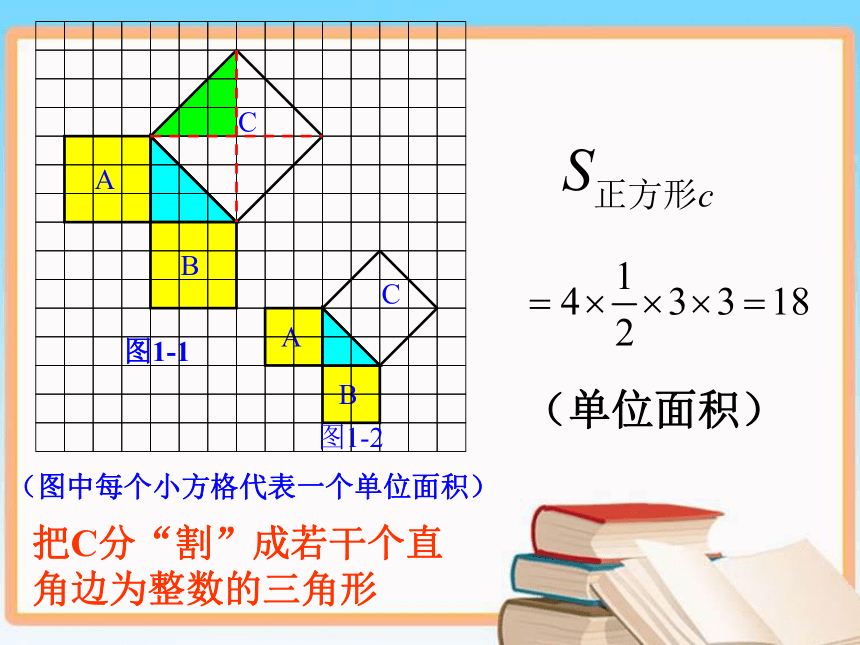
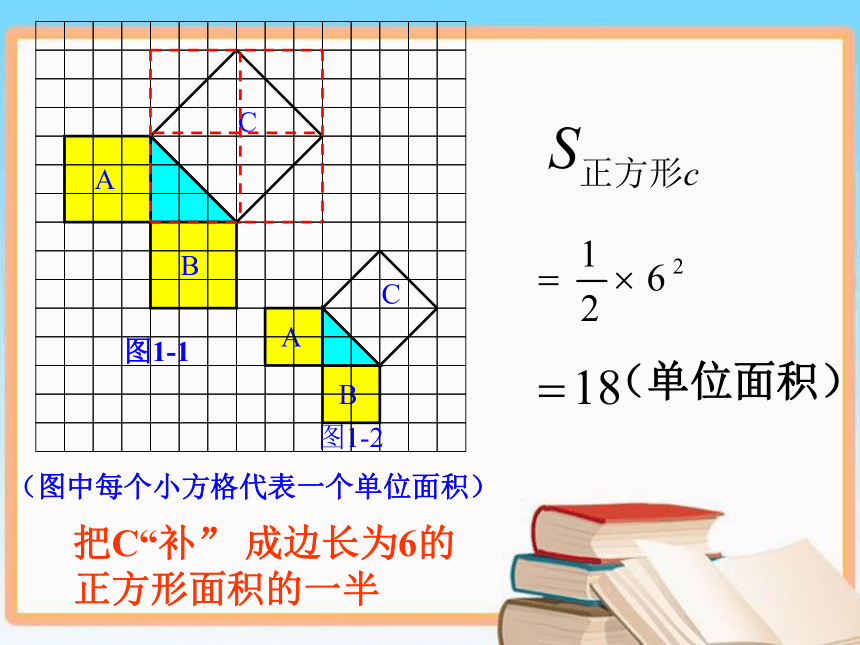
A、B、C的面积有什么关系?A的面积+B的面积=C的面积一、创设情景,兴趣导学:探究一:以等腰直角三角形三边为边的三个正方形A、B、C面积有什么关系?观察图1、图2,正方形A、B、C中各含有多少个小方格?它们的面积各是多少?你是如何得到上述结果的?与同伴交流。4489 9 18 SA+SB=SC二、尝试探索,获取新知把C分“割”成若干个直角边为整数的三角形(单位面积)(单位面积)把C“补” 成边长为6的正方形面积的一半探究二:以一般的直角三角形三边为边的正方形面积之间有什么关系呢?
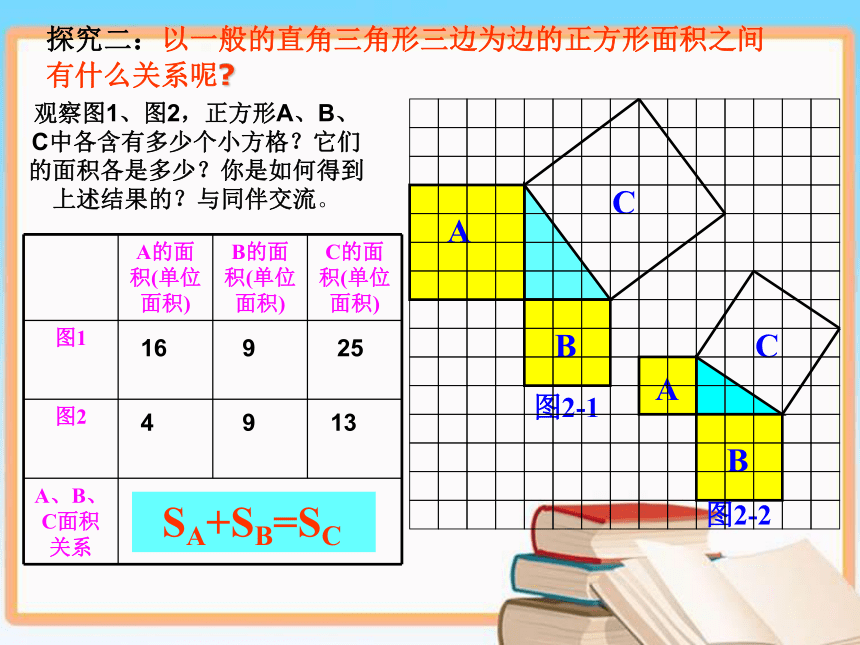
观察图1、图2,正方形A、B、C中各含有多少个小方格?它们的面积各是多少?你是如何得到上述结果的?与同伴交流。 169254913 SA+SB=SC把C分“割”成四个全等直角边为整数的直角三角形加一个小正方形(面积单位)分割法:把C“补”成边长为7的正方形减去四个全等直角三角形(面积单位) 补全法:acbSA+SB=SC 通过前面的探究,我们发现正方形A、B、C面积的关系是: 你能发现直角三角形三边 之间有什么关系吗?a2+b2=c2议一议你能用直角三角形的三边来表示这三个正方形的面积吗?SA=a2SB=b2SC=c2acba2+b2=c2┏a2+b2=c2acb 勾股定理的有关证明证明一证明二(4)(3)
(2)(1)(a-b)2(a-b)2=a2+b2-2ab = c2-2abbCa想一想:这四个直角三角形还能怎样拼?证明一 (a+b)2=a2 + b2 + 2ab = c2+2ab可得: a2 + b2 = c2证明二三、挑战自我 收获无处不在我知道了… …我感受了… …我做了… …谢谢聆听
A、B、C的面积有什么关系?A的面积+B的面积=C的面积一、创设情景,兴趣导学:探究一:以等腰直角三角形三边为边的三个正方形A、B、C面积有什么关系?观察图1、图2,正方形A、B、C中各含有多少个小方格?它们的面积各是多少?你是如何得到上述结果的?与同伴交流。4489 9 18 SA+SB=SC二、尝试探索,获取新知把C分“割”成若干个直角边为整数的三角形(单位面积)(单位面积)把C“补” 成边长为6的正方形面积的一半探究二:以一般的直角三角形三边为边的正方形面积之间有什么关系呢?
观察图1、图2,正方形A、B、C中各含有多少个小方格?它们的面积各是多少?你是如何得到上述结果的?与同伴交流。 169254913 SA+SB=SC把C分“割”成四个全等直角边为整数的直角三角形加一个小正方形(面积单位)分割法:把C“补”成边长为7的正方形减去四个全等直角三角形(面积单位) 补全法:acbSA+SB=SC 通过前面的探究,我们发现正方形A、B、C面积的关系是: 你能发现直角三角形三边 之间有什么关系吗?a2+b2=c2议一议你能用直角三角形的三边来表示这三个正方形的面积吗?SA=a2SB=b2SC=c2acba2+b2=c2┏a2+b2=c2acb 勾股定理的有关证明证明一证明二(4)(3)
(2)(1)(a-b)2(a-b)2=a2+b2-2ab = c2-2abbCa想一想:这四个直角三角形还能怎样拼?证明一 (a+b)2=a2 + b2 + 2ab = c2+2ab可得: a2 + b2 = c2证明二三、挑战自我 收获无处不在我知道了… …我感受了… …我做了… …谢谢聆听
