青岛版数学八年级下册10.3 一次函数的性质 课件(25张ppt)
文档属性
| 名称 | 青岛版数学八年级下册10.3 一次函数的性质 课件(25张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-18 10:49:18 | ||
图片预览






文档简介
课件25张PPT。10.3 一次函数的性质青岛版数学八年级下册学习目标了解一次函数的性质,并能应用它解决实际问题,体会数形结合思想.1.作函数图象的步骤是什么?(1)列表 (2)描点 (3)连线2.一次函数图象的特点是什么?
是一条直线,所以我们在作一次图象的时候只需要确定两个点,再过这两 个点作直线就可以了。知识回顾二.尝试探索1.在同一坐标系中作出正比例函数 y=0.5x , y=x ,y=3x和
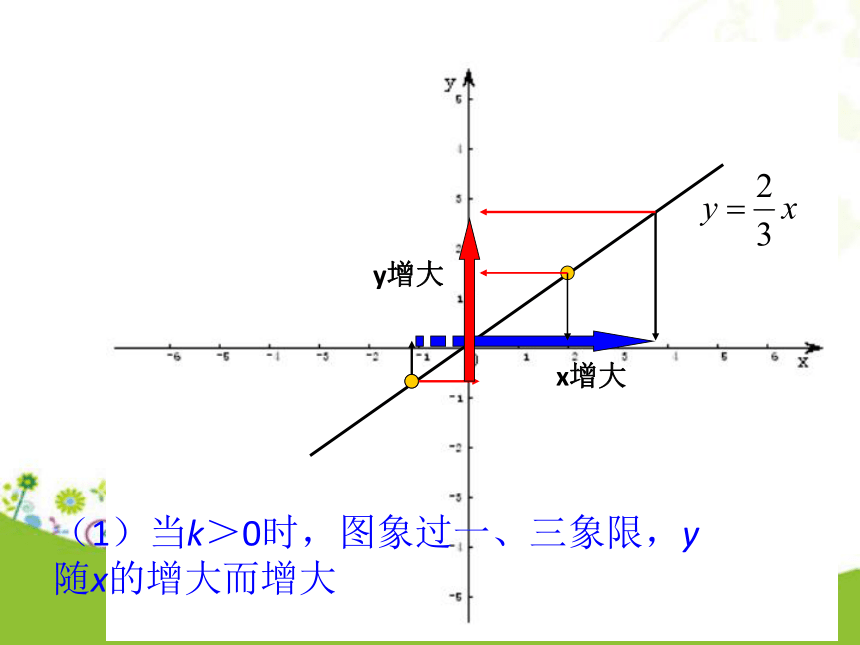
y= –2x , y=-x的图象-6o-446246-2-2-4xy2y=0.5xy=xy=3xy=-2xy=-xx增大y增大(1)当k>0时,图象过一、三象限,y随x的增大而增大x增大y减少(2) 当k<0时,图象过二、四象限,y随x的增大而_____。减小-6o-446246-2-2-4xy2y=0.5xy=xy=3xy=-2x正比例函数性质当k>0,图象过一、三象限;y随x的增大而增大。
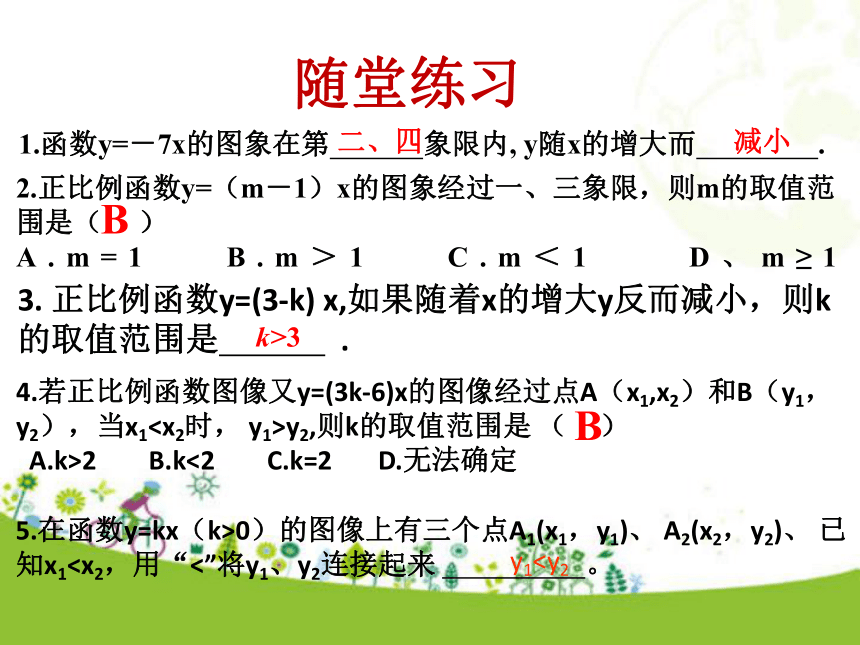
当k<0,图象过二、四象限y随x增大而减小。y=-x2.正比例函数y=(m-1)x的图象经过一、三象限,则m的取值范围是( )
A.m=1 B.m>1 C.m<1 D、m≥1B 1.函数y=-7x的图象在第 象限内, y随x的增大而 .二、四减小3. 正比例函数y=(3-k) x,如果随着x的增大y反而减小,则k的取值范围是 .k>34.若正比例函数图像又y=(3k-6)x的图像经过点A(x1,x2)和B(y1,y2),当x1y2,则k的取值范围是 ( )
A.k>2 B.k<2 C.k=2 D.无法确定5.在函数y=kx(k>0)的图像上有三个点A1(x1,y1)、 A2(x2,y2)、 已知x1?(1)当k>0时,y随x的增大而_____ ;
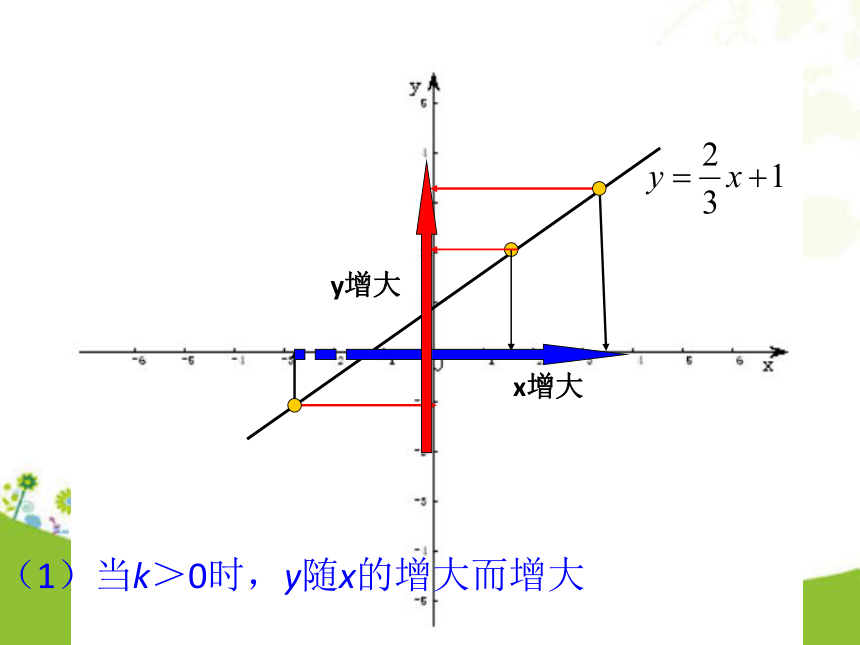
?(2)当k<0时,y随x的增大而_____。减小增大(1) 在同一坐标系中作出下列函数的图象(1)(2)(3)-3o-223123-1-1-2xy1思考:k,b的值跟图象有什么关系?(2)直线y=-x与y=-x+6的位置关系如何?-6o-446246-2-2-4xy2y=-x+6y=-x平行(2)在同一坐标系中作出下列函数的图象(1)(2)(3)-3o-223123-1-1-2xy1K>0b=0b>0b<0b=0b>0b<0通过作以上一次函数的图象我们发现y=kx+b
中,k,b的取值跟图象的关系如下:K<0一,三一,二,三一,三,四二,四一,二,四二,三,四当k>0时,y的值随x的增大而增大当k<0时,y的值随x的增大而减小(3)在平面直角坐标系中,函数y=-2x+3的图象经过( )
A.一、二、三象限 B.二、三、四象限
C.一、三、四象限 D.一、二、四象限已知一次函数y=x-2的大致图象为 ( ) A B C DCD随堂练习下列函数中,y的值随x值的增大而增大的函数是________. A.y=-2x B.y=-2x+1 C.y=x-2 D.y=-x-2C直线y=3x-2可由直线y=3x向 平移 2个单位得到。直线y=x+2可由直线y=x-1向______平移_______个单位得到。下上3确定y=kx+b中k,b的符号 k > 0 b > 0O k < 0 b <0确定y=kx+b中k,b的符号O k > 0 b < 0确定y=kx+b中k,b的符号 k < 0 b > 0确定y=kx+b中k,b的符号直线y=kx+b不经过第四象限,判断k,b的符号 k > 0 b ≥0(1)对于函数y=-5+6x, y的值随x的值增大而_________ 增大(2)函数y=2x-1的图象不经过第___ 象限二(3)对于函数y=5x+6,y随x的减小而_____减小(4)函数y=2x-1经过 象限。一、三、四填空题(5)函数y=(k-2)x - 1+k经过第一、二、 四象限, k的范围是______ 1<k<2本节课的主要内容有:1.正比例函数的特点是什么?2.一次函数及其图象的性质有哪些?3.函数图象的位置关系有几种?4.关于函数y=kx+b图象的大致
位置跟k,b的关系。谢谢!
是一条直线,所以我们在作一次图象的时候只需要确定两个点,再过这两 个点作直线就可以了。知识回顾二.尝试探索1.在同一坐标系中作出正比例函数 y=0.5x , y=x ,y=3x和
y= –2x , y=-x的图象-6o-446246-2-2-4xy2y=0.5xy=xy=3xy=-2xy=-xx增大y增大(1)当k>0时,图象过一、三象限,y随x的增大而增大x增大y减少(2) 当k<0时,图象过二、四象限,y随x的增大而_____。减小-6o-446246-2-2-4xy2y=0.5xy=xy=3xy=-2x正比例函数性质当k>0,图象过一、三象限;y随x的增大而增大。
当k<0,图象过二、四象限y随x增大而减小。y=-x2.正比例函数y=(m-1)x的图象经过一、三象限,则m的取值范围是( )
A.m=1 B.m>1 C.m<1 D、m≥1B 1.函数y=-7x的图象在第 象限内, y随x的增大而 .二、四减小3. 正比例函数y=(3-k) x,如果随着x的增大y反而减小,则k的取值范围是 .k>34.若正比例函数图像又y=(3k-6)x的图像经过点A(x1,x2)和B(y1,y2),当x1
A.k>2 B.k<2 C.k=2 D.无法确定5.在函数y=kx(k>0)的图像上有三个点A1(x1,y1)、 A2(x2,y2)、 已知x1
?(2)当k<0时,y随x的增大而_____。减小增大(1) 在同一坐标系中作出下列函数的图象(1)(2)(3)-3o-223123-1-1-2xy1思考:k,b的值跟图象有什么关系?(2)直线y=-x与y=-x+6的位置关系如何?-6o-446246-2-2-4xy2y=-x+6y=-x平行(2)在同一坐标系中作出下列函数的图象(1)(2)(3)-3o-223123-1-1-2xy1K>0b=0b>0b<0b=0b>0b<0通过作以上一次函数的图象我们发现y=kx+b
中,k,b的取值跟图象的关系如下:K<0一,三一,二,三一,三,四二,四一,二,四二,三,四当k>0时,y的值随x的增大而增大当k<0时,y的值随x的增大而减小(3)在平面直角坐标系中,函数y=-2x+3的图象经过( )
A.一、二、三象限 B.二、三、四象限
C.一、三、四象限 D.一、二、四象限已知一次函数y=x-2的大致图象为 ( ) A B C DCD随堂练习下列函数中,y的值随x值的增大而增大的函数是________. A.y=-2x B.y=-2x+1 C.y=x-2 D.y=-x-2C直线y=3x-2可由直线y=3x向 平移 2个单位得到。直线y=x+2可由直线y=x-1向______平移_______个单位得到。下上3确定y=kx+b中k,b的符号 k > 0 b > 0O k < 0 b <0确定y=kx+b中k,b的符号O k > 0 b < 0确定y=kx+b中k,b的符号 k < 0 b > 0确定y=kx+b中k,b的符号直线y=kx+b不经过第四象限,判断k,b的符号 k > 0 b ≥0(1)对于函数y=-5+6x, y的值随x的值增大而_________ 增大(2)函数y=2x-1的图象不经过第___ 象限二(3)对于函数y=5x+6,y随x的减小而_____减小(4)函数y=2x-1经过 象限。一、三、四填空题(5)函数y=(k-2)x - 1+k经过第一、二、 四象限, k的范围是______ 1<k<2本节课的主要内容有:1.正比例函数的特点是什么?2.一次函数及其图象的性质有哪些?3.函数图象的位置关系有几种?4.关于函数y=kx+b图象的大致
位置跟k,b的关系。谢谢!
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
