鲁教版(五四制)七年级下册8.5 平行线的性质定理 课件(16张PPT)
文档属性
| 名称 | 鲁教版(五四制)七年级下册8.5 平行线的性质定理 课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 186.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 15:23:12 | ||
图片预览




文档简介
课件16张PPT。8.5 平行线的性质定理定理:
同位角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.定理:
内错角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.定理:
同旁内角互补,两直线平行.
∵∠1+∠2=1800 , ∴ a∥b. 平行线的判定 如果我们把平行线的判定定理的条件和结论互换之后得到的命题是真命题吗?定理:两条平行线被第三条直线所截,同位角相等。
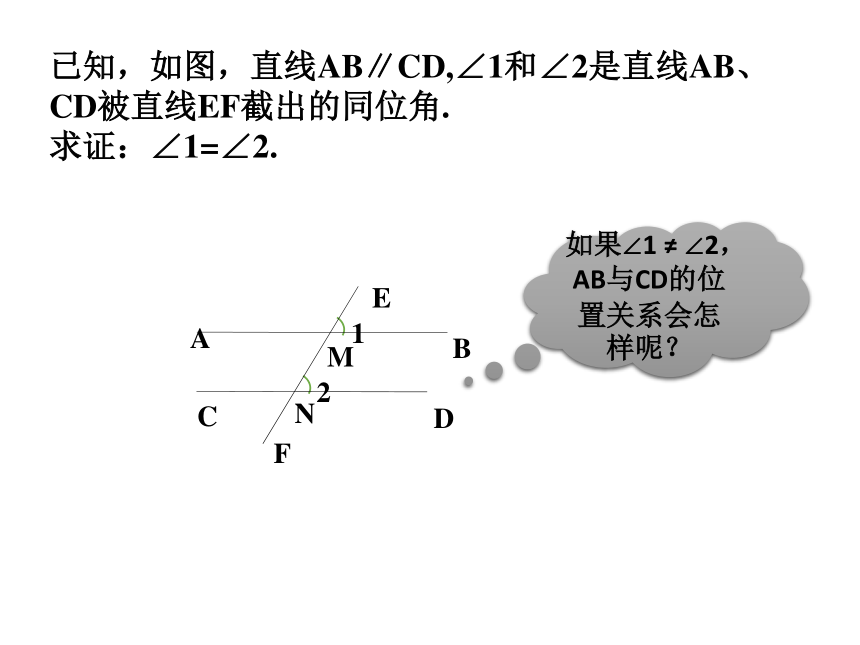
简述为:两直线平行,同位角相等。你能证明此定理吗?已知,如图,直线AB∥CD,∠1和∠2是直线AB、CD被直线EF截出的同位角.
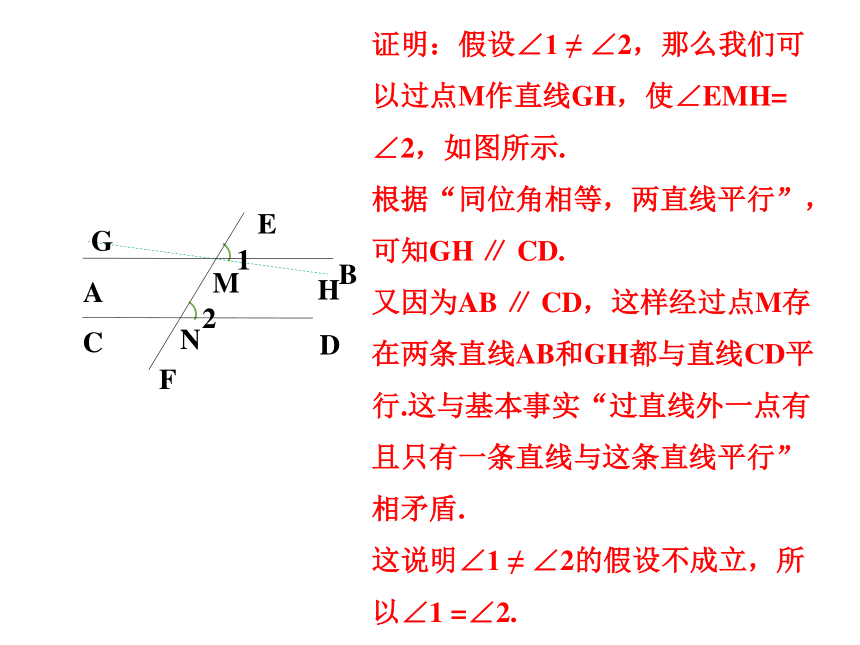
求证:∠1=∠2.如果∠1 ≠ ∠2,AB与CD的位置关系会怎样呢?证明:假设∠1 ≠ ∠2,那么我们可以过点M作直线GH,使∠EMH= ∠2,如图所示.
根据“同位角相等,两直线平行”,可知GH ∥ CD.
又因为AB ∥ CD,这样经过点M存在两条直线AB和GH都与直线CD平行.这与基本事实“过直线外一点有且只有一条直线与这条直线平行”相矛盾.
这说明∠1 ≠ ∠2的假设不成立,所以∠1 =∠2.议一议:
利用这个公理,你能证明哪些熟悉的结论?两直线平行,内错角相等。
两直线平行,同旁内角互补。 想一想:
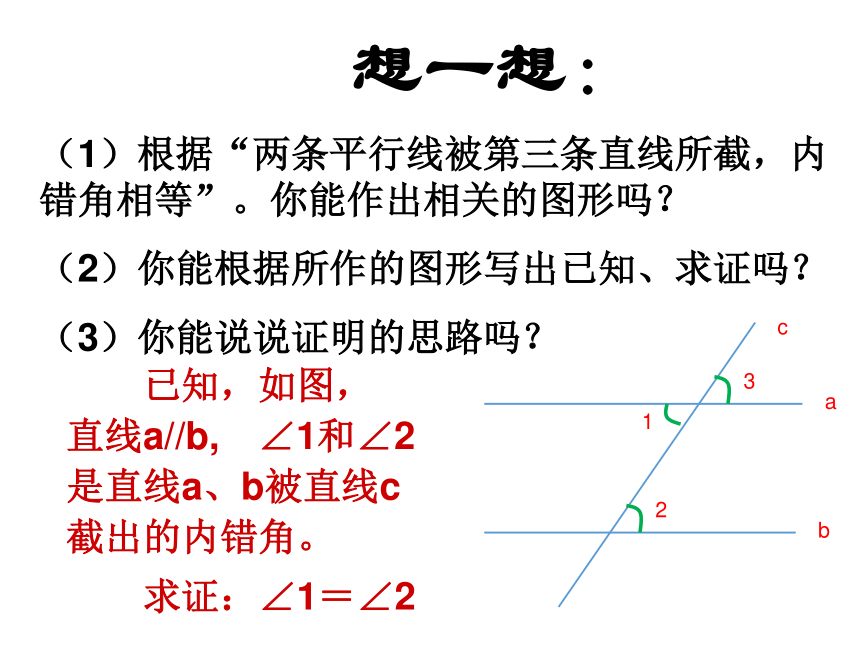
(1)根据“两条平行线被第三条直线所截,内错角相等”。你能作出相关的图形吗?
(2)你能根据所作的图形写出已知、求证吗?
(3)你能说说证明的思路吗? 已知,如图, 直线a//b, ∠1和∠2是直线a、b被直线c截出的内错角。
求证:∠1=∠2 已知:如图,直线a∥b, ∠1和∠2
是直线a、b被直线 c截出的内错角 .
求证:∠1=∠2123abc证明:∵a∥b ( )∴∠3=∠2
( )∵ ∠3=∠1 ( )∴∠1=∠2 ( )已知两直线平行,同位角相等对顶角相等等量代换做一做:
两条平行线被第三条直线所截,同旁内角互补. 已知:如图,直线a//b,∠1和∠2是直线a,b被直线c截出的同旁内角.
求证:∠1+∠2=180° 证明的一般步骤:
第一步:根据题意,画出图形.
先根据命题的条件即已知事项,画出图形,再把命题的结论即求证的需要在图上标出必要的字母或符号,以便于叙述或推理过程的表达.
第二步:根据条件、结论、结合图形,写出已知、求证。
把命题的条件化为几何符号的语言写在已知中,命题的结论转化为几何符号的语言写在求证中.
第三步:经过分析,找出由已知推出求证的途径,写出证明过程.
一般情况下,分析的过程不要求写出来,有些题目中,已 经画出了图形,写好了已知,求证,这时只要写出“证明”一项就可以了.
谈谈你的收获?2.证明的一般步骤
(1)根据题意,画出图形.
(2)根据条件、结论,结合图形,写出已知、求证。
(3)经过分析,找出由已知推出求证的途径,写出
证明过程. 根据下列命题,画出图形,并结合图形
写出已知、求证(不写证明过程):
1)垂直于同一直线的两直线平行; 已知:直线b⊥a , c⊥aabc 求证:b∥c2)一个角的平分线上的点到这个角的两
边的距离相等;已知:如图,OC是∠AOB的平分线,
EF⊥OA于F ,
EG⊥OB于G
求证:EF=EG3)如果两条直线都和第三条直线平行,
那么这两条直线也互相平行。已知:如图,直线a,b,c被直线d所
截,且a∥b,c∥b,
求证:a∥cabcd
同位角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.定理:
内错角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.定理:
同旁内角互补,两直线平行.
∵∠1+∠2=1800 , ∴ a∥b. 平行线的判定 如果我们把平行线的判定定理的条件和结论互换之后得到的命题是真命题吗?定理:两条平行线被第三条直线所截,同位角相等。
简述为:两直线平行,同位角相等。你能证明此定理吗?已知,如图,直线AB∥CD,∠1和∠2是直线AB、CD被直线EF截出的同位角.
求证:∠1=∠2.如果∠1 ≠ ∠2,AB与CD的位置关系会怎样呢?证明:假设∠1 ≠ ∠2,那么我们可以过点M作直线GH,使∠EMH= ∠2,如图所示.
根据“同位角相等,两直线平行”,可知GH ∥ CD.
又因为AB ∥ CD,这样经过点M存在两条直线AB和GH都与直线CD平行.这与基本事实“过直线外一点有且只有一条直线与这条直线平行”相矛盾.
这说明∠1 ≠ ∠2的假设不成立,所以∠1 =∠2.议一议:
利用这个公理,你能证明哪些熟悉的结论?两直线平行,内错角相等。
两直线平行,同旁内角互补。 想一想:
(1)根据“两条平行线被第三条直线所截,内错角相等”。你能作出相关的图形吗?
(2)你能根据所作的图形写出已知、求证吗?
(3)你能说说证明的思路吗? 已知,如图, 直线a//b, ∠1和∠2是直线a、b被直线c截出的内错角。
求证:∠1=∠2 已知:如图,直线a∥b, ∠1和∠2
是直线a、b被直线 c截出的内错角 .
求证:∠1=∠2123abc证明:∵a∥b ( )∴∠3=∠2
( )∵ ∠3=∠1 ( )∴∠1=∠2 ( )已知两直线平行,同位角相等对顶角相等等量代换做一做:
两条平行线被第三条直线所截,同旁内角互补. 已知:如图,直线a//b,∠1和∠2是直线a,b被直线c截出的同旁内角.
求证:∠1+∠2=180° 证明的一般步骤:
第一步:根据题意,画出图形.
先根据命题的条件即已知事项,画出图形,再把命题的结论即求证的需要在图上标出必要的字母或符号,以便于叙述或推理过程的表达.
第二步:根据条件、结论、结合图形,写出已知、求证。
把命题的条件化为几何符号的语言写在已知中,命题的结论转化为几何符号的语言写在求证中.
第三步:经过分析,找出由已知推出求证的途径,写出证明过程.
一般情况下,分析的过程不要求写出来,有些题目中,已 经画出了图形,写好了已知,求证,这时只要写出“证明”一项就可以了.
谈谈你的收获?2.证明的一般步骤
(1)根据题意,画出图形.
(2)根据条件、结论,结合图形,写出已知、求证。
(3)经过分析,找出由已知推出求证的途径,写出
证明过程. 根据下列命题,画出图形,并结合图形
写出已知、求证(不写证明过程):
1)垂直于同一直线的两直线平行; 已知:直线b⊥a , c⊥aabc 求证:b∥c2)一个角的平分线上的点到这个角的两
边的距离相等;已知:如图,OC是∠AOB的平分线,
EF⊥OA于F ,
EG⊥OB于G
求证:EF=EG3)如果两条直线都和第三条直线平行,
那么这两条直线也互相平行。已知:如图,直线a,b,c被直线d所
截,且a∥b,c∥b,
求证:a∥cabcd
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
