湘教版 八下数学2.1多边形课时练学案(PDF版含答案)
文档属性
| 名称 | 湘教版 八下数学2.1多边形课时练学案(PDF版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 15:18:15 | ||
图片预览



文档简介
"!
!
多边形! "
!前置诊断"检测你的基础#助力新课学习
!
!!
四边形的内角和是 %
!!
&
*!$2"( ,!&""( .!+-"( /!)"(
"!
如图
&!$ $ $
!在
"
#$%
中!
#
#'!"(
!
#
$'-!(
!则
#
#%&
的度数为 %
!!
&
*!-!( ,!2!( .!$$!( /!$+!(
图
&!$ $ $
!!!!!!! 图
&!$ $ &
#!
如图
&!$ $ &
!在
45
"
#$%
中!
#
%'1"(
!
&'
$
#$
于
'
!交
#%
于
&!
若
#
$'!+(
!
则
#
%&'
的度数为 %
!!
&
*!+( ,!$&3( .!$)+( /!$)3(
!前置巩固"如果你没有全部正确#务必回顾复习
!
$!
三角形内角和为
$2"(
!而四边形内角和可以转化为两个三角形的内角和!所以四
边形的内角和为
+-"(!
&!
三角形的一个外角等于与它不相邻的两内角和
!
!!
前面我们已学过了三角形+四边形的内角和#并且知道四边形的内角和就是将它转
化为两个三角形的内角和#那么五边形+六边形+
3
边形的内角和怎么求呢$
!!
多边形的对角线
连接不相邻的两个顶点的线段!叫作多边形的对角线
!
从
3
边形的一个顶点出发有%
36+
&条对角线!从而
3
边形被分成了%
36&
&个三
角形
!
"!
多边形内角和定理
将一个
3
边形沿一个顶点的对角线分成%
36&
&个三角形!从而得到了
3
边形的内角
和公式"%
36&
&.
$2"(
!其中运用了三角形内角和定理
!
除利用对角线把多边形分成几个
三角形外!还有其他方法也可以得到
3
边形的内角和公式
!
如图
&!$ $ +
!在
3
边形内任取一点
+
!与多边形各顶点连接!把
3
边形分成
3
个三角
形!用
3
个三角形的内角和
3
.
$2"(
减去中心的周角
+-"(
!得
3
边形的内角和为%
36&
&.
$2"(!
图
&!$ $ +
综上可得!推导多边形的内角和公式!都是利用转化思想!即把多边形分成若干个三
角形!从而将多边形问题转化为三角形问题来解决
!
!!
若一个多边形的内角和是
&$-"(
!则这个多边形的边数是多少#
"!&"$2
年世界杯在莫斯科召开!绘制一个内角和为
&"$2(
的多边形图案有可能吗#
#!
已知一个多边形除了一个内角外!其余各内角的和是
&"$-(
!它是几边形#
$!
从
3
边形一个顶点出发可以引出%
36+
&条对角线!从而可知
3
边形的对角线一共有
3
%
36+
&
&
条
!
&!
从
3
边形一个顶点出发的所有对角线将
3
边形分成%
36&
&个三角形!进而得到
3
边形的内角和为%
36&
&.
$2"(!
+!
将多边形的内角和转化为多个三角形的内角和!这是将未学过的知识转化为已经
学过的知识!这就是转化思想的运用
!
)!
在解决数学问题时!可以通过设元寻找已知与未知之间的等量关系!构造方程或
不等式!然后求解方程或不等式完成未知向已知的转化
!
!!
已知两个多边形的内角和为
$2""(
!且两多边形的边数之比为
&%!
!则这两个多边形
的边数分别为
!!!!!!!!
!
"!
一个凸
3
边形除了一个内角之外!其余各内角之和是
$32"(
!则这个多边形的边数
3'
!!!!!
!这个内角的度数为
!!!!!
!
#!
如图
&!$ $ )
!求
#
#0
#
$0
#
%0
#
&0
#
'0
#
(
的度数
!
!
图
&!$ $ )
$!
如图
&!$ $ !
!求
#
#0
#
$0
#
%0
#
&0
#
'0
#
(0
#
4
的度数
!
!
图
&!$ $ !
"!
!
多边形!
"
"
!前置诊断"检测你的基础#助力新课学习
!
!!
一个多边形的内角和是
3&"(
!这个多边形是%
!!
&边形
!
*!
四
,!
五
.!
六
/!
七
"!
如图
&!$ & $
!在
"
#$%
中!
%&
$
#$
!
%'
平分
#
#%$
!
#
$'!"(
!
#
#'&"(
!则
#
&%'
的度数为 %
!!
&
图
&!$ & $
*!3"( ,!"( .!+"( /!$!(
!前置巩固"如果你没有全部正确#务必回顾复习
!
$!3
边形的内角和等于%
36&
&.
$2"(!
&!
三角形的一个外角等于与它不相邻的两个内角之和
!
!!
我们知道三角形的外角和是
+-"(
#四边形的外角和是
+-"(
#那么
3
边形的外角和是
+-"(
吗$
3
边形的外角和与边数是什么关系呢$
!!
多边形的外角的概念
多边形的内角的一边与另一边的反向延长线组成的角!叫作多边形的一个外角
!
多边形每个顶点处有两个外角!这两个外角互为对顶角
!
"!
多边形的外角和
在多边形的每个顶点处取一个外角!它们的和叫作这个多边形的外角和
!
#!
多边形的外角和等于
#'&(
对于一个
3
边形!因为任一外角与它相邻的内角之和为
$2"(
!
3
边形的内角和等于
%
36&
&.
$2"(
!故外角和等于
3
.
$2"(6
%
36&
&.
$2"(!
由此得出"任意多边形的外角和等于
+-"(!
3
边形的外角和与边数没有关系!是一个定值
!
!!
一个正多边形每个外角都是
-"(
!求这个多边形的边数
!
"!
一个正多边形每个内角都是
$+!(
!求这个多边形的边数
!
#!
一个正多边形的每一个内角都比相邻的外角大
+-(
!求这个正多边形的边数
!
!
图
&!$ & &
$!
如图
&!$ & &
!求
#
#0
#
$0
#
%0
#
&0
#
'0
#
(
的度数
!
$!
任意多边形的外角和等于
+-"(!
&!
三角形的一个外角等于与它不相邻的两内角和!和与它相邻的内角互补
!
+!
有时可以将多边形的内角转化为与它相邻的外角!然后再利用外角和进行计算
!
!!
一个十边形所有内角都相等!求它的外角大小
!
"!
一个多边形的每一个外角都是
3&(
!求这个多边形的内角和
!
#!
如图
&!$ & +
!求
#
#0
#
$0
#
%0
#
&0
#
'0
#
(0
#
40
#
5
的度数
!
!
图
&!$ & +
!
图
&!$ & )
$!
如图
&!$ & )
!若
#
#'
#
$'
#
%'
#
&'
#
'
!求
#
#!
! ! ! ! !
!
!
!
! ! !
!
第
"
章
!
四边形
"!
78%
!"
!前置诊断"
!!*
!
"!*
!
#!"
!变式训练"
!!',
"!
设多边形的边数是
5
#则
!
54(
"
5'$+-(+'$!
15-'#
'2
2+
!
.5
不是整数#
1
不可能
!
#!
设多边形的边数为
5
#则
+
%
!
54(
"
5'$+4(+'3
%
'$+
#
解得
'#
'
)
%
5
%
',
'
)
!
.
多边形的边数是正整数#
1
它是十四边形
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
& !
!效果检测"
!!,
#
'+
!
设两个多边形的边数分别为
-
#
6
#由题意可知$
!
-4(
"
5'$+8
!
6
4(
"
5'$+-'$++
#
-A
6
-(A)
'
#
解得--,#
6
-'+
'
!
"!'(
!
(+%
由题意可得
+
%
!
54(
"
5'$+4'9$+
%
'$+
#
解得
''
$
2
%
5
%
'(
$
2
!
从而可知
5-'(!
则这个内角的度数为!
54(
"
5'$+%4'9$+%-(+%!
#!
连接
%/!
由三角形内角和可知
"
"8
"
$-
"
'%/8
"
'/%!
1
"
"8
"
$8
"
%8
"
#8
"
,8
"
/-
"
'%/8
"
'/%8
"
#%$8
"
,/"8
"
#8
"
,-#3+%
!四边形内角和为
#3+%
"
!
$!
连接
"$!
"
"8
"
$8
"
%8
"
#8
"
,8
"
/8
"
0-
!
"
"8
"
$8
"
#8
"
/
"
8
!
"
%8
"
,8
"
0
"
-
#3+%4
!
"
%"$8
"
0$"
"
8#3+%4
!
'$+%4
"
%"$4
"
0$"
"
-),+%!
"!
78%
!
"
"
!前置诊断"
!!*
"!!
!
由三角形内角和可知$
"
"%$-'$+%4
"
"4
"
$-''+%
#同理可得
"
"%#-9+%!
.%,
平分
"
"%$
#
1
"
"%,-
'
(
"
"%$-))%
#
从而
"
#%,-
"
"%#4
"
"%,-')%!
!变式训练"
!!3
!
"!$
#!)
!
设正多边形一个外角为
-%
#则!
'$+4-
"
4
--#3
#解得
--9(!
15-#3+;9(-)!
$!.
"
"8
"
$-
"
"04
#
"
%8
"
#-
"
#14
#
"
,8
"
/-
"
/40
#
1
"
"8
"
$8
"
%8
"
#8
"
,8
"
/-
"
"048
"
#148
"
/40-#3+%!
!效果检测"
!!#3%
!
"!),+%
!
#!#3+%
$!.
"
"8
"
%
和
"
$8
"
#
都是
"
,
所在的小
三角形的内角#
1
"
"8
"
$8
"
%8
"
#8
"
,-'$+%!
又
.
"
"-
"
$-
"
%-
"
#-
"
,
#
1
"
"-'$+%;)-#3%!
!
!
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
!
多边形! "
!前置诊断"检测你的基础#助力新课学习
!
!!
四边形的内角和是 %
!!
&
*!$2"( ,!&""( .!+-"( /!)"(
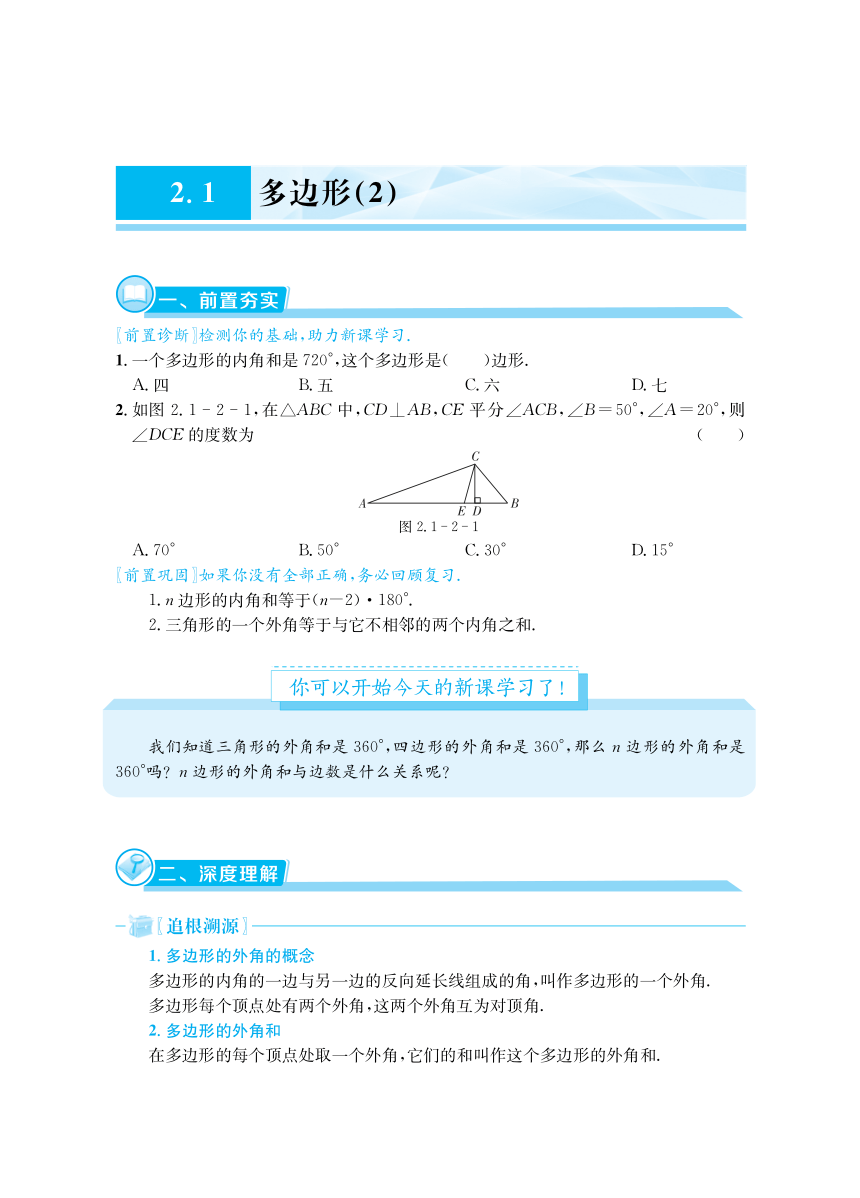
"!
如图
&!$ $ $
!在
"
#$%
中!
#
#'!"(
!
#
$'-!(
!则
#
#%&
的度数为 %
!!
&
*!-!( ,!2!( .!$$!( /!$+!(
图
&!$ $ $
!!!!!!! 图
&!$ $ &
#!
如图
&!$ $ &
!在
45
"
#$%
中!
#
%'1"(
!
&'
$
#$
于
'
!交
#%
于
&!
若
#
$'!+(
!
则
#
%&'
的度数为 %
!!
&
*!+( ,!$&3( .!$)+( /!$)3(
!前置巩固"如果你没有全部正确#务必回顾复习
!
$!
三角形内角和为
$2"(
!而四边形内角和可以转化为两个三角形的内角和!所以四
边形的内角和为
+-"(!
&!
三角形的一个外角等于与它不相邻的两内角和
!
!!
前面我们已学过了三角形+四边形的内角和#并且知道四边形的内角和就是将它转
化为两个三角形的内角和#那么五边形+六边形+
3
边形的内角和怎么求呢$
!!
多边形的对角线
连接不相邻的两个顶点的线段!叫作多边形的对角线
!
从
3
边形的一个顶点出发有%
36+
&条对角线!从而
3
边形被分成了%
36&
&个三
角形
!
"!
多边形内角和定理
将一个
3
边形沿一个顶点的对角线分成%
36&
&个三角形!从而得到了
3
边形的内角
和公式"%
36&
&.
$2"(
!其中运用了三角形内角和定理
!
除利用对角线把多边形分成几个
三角形外!还有其他方法也可以得到
3
边形的内角和公式
!
如图
&!$ $ +
!在
3
边形内任取一点
+
!与多边形各顶点连接!把
3
边形分成
3
个三角
形!用
3
个三角形的内角和
3
.
$2"(
减去中心的周角
+-"(
!得
3
边形的内角和为%
36&
&.
$2"(!
图
&!$ $ +
综上可得!推导多边形的内角和公式!都是利用转化思想!即把多边形分成若干个三
角形!从而将多边形问题转化为三角形问题来解决
!
!!
若一个多边形的内角和是
&$-"(
!则这个多边形的边数是多少#
"!&"$2
年世界杯在莫斯科召开!绘制一个内角和为
&"$2(
的多边形图案有可能吗#
#!
已知一个多边形除了一个内角外!其余各内角的和是
&"$-(
!它是几边形#
$!
从
3
边形一个顶点出发可以引出%
36+
&条对角线!从而可知
3
边形的对角线一共有
3
%
36+
&
&
条
!
&!
从
3
边形一个顶点出发的所有对角线将
3
边形分成%
36&
&个三角形!进而得到
3
边形的内角和为%
36&
&.
$2"(!
+!
将多边形的内角和转化为多个三角形的内角和!这是将未学过的知识转化为已经
学过的知识!这就是转化思想的运用
!
)!
在解决数学问题时!可以通过设元寻找已知与未知之间的等量关系!构造方程或
不等式!然后求解方程或不等式完成未知向已知的转化
!
!!
已知两个多边形的内角和为
$2""(
!且两多边形的边数之比为
&%!
!则这两个多边形
的边数分别为
!!!!!!!!
!
"!
一个凸
3
边形除了一个内角之外!其余各内角之和是
$32"(
!则这个多边形的边数
3'
!!!!!
!这个内角的度数为
!!!!!
!
#!
如图
&!$ $ )
!求
#
#0
#
$0
#
%0
#
&0
#
'0
#
(
的度数
!
!
图
&!$ $ )
$!
如图
&!$ $ !
!求
#
#0
#
$0
#
%0
#
&0
#
'0
#
(0
#
4
的度数
!
!
图
&!$ $ !
"!
!
多边形!
"
"
!前置诊断"检测你的基础#助力新课学习
!
!!
一个多边形的内角和是
3&"(
!这个多边形是%
!!
&边形
!
*!
四
,!
五
.!
六
/!
七
"!
如图
&!$ & $
!在
"
#$%
中!
%&
$
#$
!
%'
平分
#
#%$
!
#
$'!"(
!
#
#'&"(
!则
#
&%'
的度数为 %
!!
&
图
&!$ & $
*!3"( ,!"( .!+"( /!$!(
!前置巩固"如果你没有全部正确#务必回顾复习
!
$!3
边形的内角和等于%
36&
&.
$2"(!
&!
三角形的一个外角等于与它不相邻的两个内角之和
!
!!
我们知道三角形的外角和是
+-"(
#四边形的外角和是
+-"(
#那么
3
边形的外角和是
+-"(
吗$
3
边形的外角和与边数是什么关系呢$
!!
多边形的外角的概念
多边形的内角的一边与另一边的反向延长线组成的角!叫作多边形的一个外角
!
多边形每个顶点处有两个外角!这两个外角互为对顶角
!
"!
多边形的外角和
在多边形的每个顶点处取一个外角!它们的和叫作这个多边形的外角和
!
#!
多边形的外角和等于
#'&(
对于一个
3
边形!因为任一外角与它相邻的内角之和为
$2"(
!
3
边形的内角和等于
%
36&
&.
$2"(
!故外角和等于
3
.
$2"(6
%
36&
&.
$2"(!
由此得出"任意多边形的外角和等于
+-"(!
3
边形的外角和与边数没有关系!是一个定值
!
!!
一个正多边形每个外角都是
-"(
!求这个多边形的边数
!
"!
一个正多边形每个内角都是
$+!(
!求这个多边形的边数
!
#!
一个正多边形的每一个内角都比相邻的外角大
+-(
!求这个正多边形的边数
!
!
图
&!$ & &
$!
如图
&!$ & &
!求
#
#0
#
$0
#
%0
#
&0
#
'0
#
(
的度数
!
$!
任意多边形的外角和等于
+-"(!
&!
三角形的一个外角等于与它不相邻的两内角和!和与它相邻的内角互补
!
+!
有时可以将多边形的内角转化为与它相邻的外角!然后再利用外角和进行计算
!
!!
一个十边形所有内角都相等!求它的外角大小
!
"!
一个多边形的每一个外角都是
3&(
!求这个多边形的内角和
!
#!
如图
&!$ & +
!求
#
#0
#
$0
#
%0
#
&0
#
'0
#
(0
#
40
#
5
的度数
!
!
图
&!$ & +
!
图
&!$ & )
$!
如图
&!$ & )
!若
#
#'
#
$'
#
%'
#
&'
#
'
!求
#
#!
! ! ! ! !
!
!
!
! ! !
!
第
"
章
!
四边形
"!
78%
!"
!前置诊断"
!!*
!
"!*
!
#!"
!变式训练"
!!',
"!
设多边形的边数是
5
#则
!
54(
"
5'$+-(+'$!
15-'#
'2
2+
!
.5
不是整数#
1
不可能
!
#!
设多边形的边数为
5
#则
+
%
!
54(
"
5'$+4(+'3
%
'$+
#
解得
'#
'
)
%
5
%
',
'
)
!
.
多边形的边数是正整数#
1
它是十四边形
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
& !
!效果检测"
!!,
#
'+
!
设两个多边形的边数分别为
-
#
6
#由题意可知$
!
-4(
"
5'$+8
!
6
4(
"
5'$+-'$++
#
-A
6
-(A)
'
#
解得--,#
6
-'+
'
!
"!'(
!
(+%
由题意可得
+
%
!
54(
"
5'$+4'9$+
%
'$+
#
解得
''
$
2
%
5
%
'(
$
2
!
从而可知
5-'(!
则这个内角的度数为!
54(
"
5'$+%4'9$+%-(+%!
#!
连接
%/!
由三角形内角和可知
"
"8
"
$-
"
'%/8
"
'/%!
1
"
"8
"
$8
"
%8
"
#8
"
,8
"
/-
"
'%/8
"
'/%8
"
#%$8
"
,/"8
"
#8
"
,-#3+%
!四边形内角和为
#3+%
"
!
$!
连接
"$!
"
"8
"
$8
"
%8
"
#8
"
,8
"
/8
"
0-
!
"
"8
"
$8
"
#8
"
/
"
8
!
"
%8
"
,8
"
0
"
-
#3+%4
!
"
%"$8
"
0$"
"
8#3+%4
!
'$+%4
"
%"$4
"
0$"
"
-),+%!
"!
78%
!
"
"
!前置诊断"
!!*
"!!
!
由三角形内角和可知$
"
"%$-'$+%4
"
"4
"
$-''+%
#同理可得
"
"%#-9+%!
.%,
平分
"
"%$
#
1
"
"%,-
'
(
"
"%$-))%
#
从而
"
#%,-
"
"%#4
"
"%,-')%!
!变式训练"
!!3
!
"!$
#!)
!
设正多边形一个外角为
-%
#则!
'$+4-
"
4
--#3
#解得
--9(!
15-#3+;9(-)!
$!.
"
"8
"
$-
"
"04
#
"
%8
"
#-
"
#14
#
"
,8
"
/-
"
/40
#
1
"
"8
"
$8
"
%8
"
#8
"
,8
"
/-
"
"048
"
#148
"
/40-#3+%!
!效果检测"
!!#3%
!
"!),+%
!
#!#3+%
$!.
"
"8
"
%
和
"
$8
"
#
都是
"
,
所在的小
三角形的内角#
1
"
"8
"
$8
"
%8
"
#8
"
,-'$+%!
又
.
"
"-
"
$-
"
%-
"
#-
"
,
#
1
"
"-'$+%;)-#3%!
!
!
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
