湘教版 八下数学2.2平行四边形课时练学案(PDF版含答案)
文档属性
| 名称 | 湘教版 八下数学2.2平行四边形课时练学案(PDF版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 15:19:19 | ||
图片预览




文档简介
"!"
!
平行四边形! "
!前置诊断"检测你的基础#助力新课学习
!
!!
已知平行四边形的面积是
$))
!相邻两边上的高分别为
2
和
1
!则它的周长是 %
!!
&
*!$3 ,!+) .!-2 /!3&
"!
用
&"#
长的一铁丝围成一个平行四边形!使长边与短边的比为
+%&
!则短边长为
%
!!
&
*!$&# ,!2# .!-# /!)#
!前置巩固"如果你没有全部正确#务必回顾复习
!
平行四边形的周长为两邻边和的两倍
!
!!
在小学#我们已初步认识了平行四边形#平行四边形究竟具有什么样的性质呢$通过
本节课的学习#我们将更加深入地认识平行四边形
!
!!
平行四边形的定义
两组对边分别平行的四边形叫作平行四边形
!
"!
根据定义画一个平行四边形!测量平行四边形四条边的长度$四个角的大小!你能
做出什么猜测#
%
$
&猜想"通过观察和测量!发现平行四边形对边相等!对角相等'
%
&
&验证猜想
!
如图
&!& $ $
!连接
#%!
!
图
&!& $ $
:
四边形
#$%&
为平行四边形!
;#$
)
&%
!
#&
)
$%
%平行四边形的两组对边分别平行&
!
;
#
$'
#
&
!
#
+'
#
)!
又
#%'%#
!
;
"
#$%
("
%&#!
;#$'%&
!
$%'&#
!
#
$'
#
&!
又
#
$0
#
)'
#
&0
#
+
!
;
#
$#&'
#
&%$!
#!
%
$
&平行四边形边的性质"
对边平行)))平行四边形的定义'
对边相等)))连接对角线!由全等三角形证明
!
%
&
&平行四边形角的性质"
邻角互补)))两直线平行!同旁内角互补'
对角相等)))同角的补角相等!即对角相等
!
!!
如图
&!& $ &
!在
-
#$%&
中!
#$'+
!
$%'!
!
#
#$%
的平分线交
#&
于点
'
!则
&'
的长为 %
!!
&
!
图
&!& $ &
*!
,!)
.!+
/!&
"!
如图
&!& $ +
!在
-
#$%&
中!点
'
!
(
分别在
#&
!
$%
上!且
#''%(
!
'(
!
$&
相交
于点
+!
求证"
+''+(!
图
&!& $ +
$!
平行四边形的内角和为
+-"(
!外角和为
+-"(!
&!
任何一条对角线将平行四边形分成两个全等的三角形
!
+!
平行四边形的性质为证明线段相等$角相等提供了新思路$新方法
!
)!
连接对角线!把四边形转化为两个三角形是解决四边形问题的常用方法
!
!!
如图
&!& $ )
!在
-
#$%&
中!
#
$'2"(
!
#'
平分
#
$#&
交
$%
于点
'
!
%(
)
'#
交
#&
于点
(
!则
#
$
的度数为 %
!!
&
图
&!& $ )
*!)"( ,!"( .!-"( /!2"(
"!
已知平行四边形的周长为
$""8#
!两邻边之差为
+"8#
!求平行四边形各边的长
!
#!
已知"如图
&!& $ !
!在
-
#$%&
中!延长
#$
至点
'
!延长
%&
至点
(
!使得
$''
&(
!连接
'(
!与对角线
#%
交于点
+!
求证"
+''+(!
!
图
&!& $ !
"!"
!
平行四边形!
"
"
!前置诊断"检测你的基础#助力新课学习
!
!!
在
-
#$%&
中!若
#
#'-!(
!则
#
%
的度数是 %
!!
&
*!$"!( ,!$$!( .!$&!( /!-!(
!
图
&!& & $
"!
如图
&!& & $
!四边形
#$%&
为平行四边形!
(
是
%&
的中点!
连接
#(
并延长与
$%
的延长线交于点
'
!则下面的结论不正确
的是 %
!!
&
*!#&'$% ,!#&'%'
.!#&'%( /!$%'%'
!前置巩固"如果你没有全部正确#务必回顾复习
!
平行四边形两组对边分别平行且相等!对角相等
!
!!
我们知道平行四边形的两组对边分别平行且相等#对角相等#那么平行四边形还有
什么其他的性质吗$ 对角线又有怎样的性质呢$
!!
平行四边形的对角线
连接平行四边形不相邻的两顶点得到的线段是平行四边形的对角线!平行四边形有
两条对角线!且相交于一点
!
"!
平行四边形对角线的性质
!
图
&!& & &
如图
&!& & &
!
:
四边形
#$%&
是平行四边形!
;#$
)
&%
!
#$'&%
!
;
#
$'
#
&
!
#
+'
#
)
!
;
"
+#$
("
+%&!
;+#'+%
!
+$'+&!
由此得到平行四边形的对角线互相平分
!
!
图
&!& & +
!!
如图
&!& & +
!
-
#$%&
的对角线
#%
!
$&
相交于点
+
!且
#%0$&'$-
!
%&'-
!则
"
#$+
的周长是 %
!!
&
*!$" ,!$)
.!&" /!&&
"!
以长为
!8#
!
)8#
!
38#
的三条线段中的两条为边!另一条为对角线画平行四边形!可
以画出形状不同的平行四边形的个数是
!!!!
!
!
图
&!& & )
#!
如图
&!& & )
!在
-
#$%&
中!对角线
#%
!
$&
相交于点
+
!
过
+
点作
'(
分别交
#$
!
%&
于点
'
!
(
!那么
+'
!
+(
是否相
等!说明理由
!
$!
平行四边形的性质包含边$角和对角线!从这三者的关系去记忆平行四边形的性质
!
&!
平行四边形的对角线互相平分
!
!!
以下平行四边形的性质中!错误的是 %
!!
&
*!
对边平行
,!
对角相等
.!
对边相等
/!
对角线相等
!
图
&!& & !
"!
如图
&!& & !
!在
-
#$%&
中!已知
#
+&#'1"(
!
#%'$"8#
!
$&'-8#
!则
#&
的长为 %
!!
&
*!)8# ,!8#
.!-8# /!28#
#!
一个平行四边形的一个内角是它邻角的
+
倍!那么这个内角的度数是
!!!!
!
$!
已知"如图
&!& & -
!
-
#$%&
的周长为
-"8#
!对角线
#%
!
$&
相交于点
+
!
"
#+$
的周长比
"
$+%
的周长多
28#
!求
-
#$%&
各边的长
!
!
图
&!& & -
%!
已知"如图
&!& & 3
!在
-
#$%&
中!
'
!
(
分别是
$%
!
#&
上的点!且
$''&(
!
'(
交
#%
于点
+!
那么
+'
与
+(
相等吗# 为什么#
!
图
&!& & 3
"!"
!
平行四边形!
#
"
!前置诊断"检测你的基础#助力新课学习
!
!!
如图
&!& + $
!
+
是
-
#$%&
对角线的交点!
"
+$%
的周长为
!1
!
$&'+2
!
#%'&)
!
则
#&
的长是 %
!!
&
*!$& ,!$1 .!&2 /!+$
"!
如图
&!& + &
!在
"
0$2
中!
$0'-
!点
#
!
%
!
&
分别在
0$
!
$2
!
02
上!四边形
#$%&
为平行四边形!
#
2&%'
#
0&#
!则
-
#$%&
的周长是 %
!!
&
*!&) ,!$2 .!$- /!$&
图
&!& + $
!!!! 图
&!& + &
!前置巩固"如果你没有全部正确#务必回顾复习
!
平行四边形的性质"
!
两组对边分别平行且相等'
"
平行四边形的对角相等!邻角互补'
#
平行四边形的对角线互相平分
!
!!
我们已经学习了平行四边形的边+角以及对角线的相关性质#那么如何判定一个四
边形是平行四边形呢$ 它的边+角以及对角线又要满足什么条件呢$
!!
定义是判定的基本方法
利用平行四边形的定义可以判定一个四边形是不是平行四边形!即看两组对边是不
是分别平行
!
"!
平行四边形的判定定理
两组对边分别相等的四边形是平行四边形
!
只要连接对角线!利用全等!得到内错角
相等!从而证明两组对边分别平行
!
一组对边平行且相等的四边形是平行四边形
!
连接对角线!利用全等!得到另一组对
边也平行
!
!!
已知
#&'$%
!要使四边形
#$%&
是平行四边形!还需补充的一个条件是"
!!!!
!
"!
如图
&!& + +
!已知
#%
是四边形
#$%&
的对角线!
#
$#%'
#
&%#
!
#
&#%'
#
$%#
!求证"
#&'$%!
!
图
&!& + +
平行四边形的判定从边的关系来看!定义是基础!结合全等可以得到判定定理
$
和
&
!特别是一组对边平行且相等是常用的方法
!
!!
下列条件中!不能够判定一个四边形是平行四边形的是 %
!!
&
*!
两组对边分别相等
,!
两组对边分别平行
.!
一组对边平行且相等
/!
一组对边平行!另一组对边相等
"!
如图
&!& + )
!
#$
与
&%
平行且相等!
&%''('$"
!
&''%('2
!则图中的平行四
边形有
!!!!!!!!!!
!理由分别是
!!!!!!!!!!!
$
!!!!!!
!!!!!
!
图
&!& + )
#!
如图
&!& + !
!在
-
#$%&
中!
&'
$
#%
!
$(
$
#%
!证明"四边形
&'$(
为平行四
边形
!
!
图
&!& + !
"!"
!
平行四边形!
$
"
!前置诊断"检测你的基础#助力新课学习
!
!!
九根火柴棒排成如图
&!& ) $
形状!图中有
! !
个平行四边形!你判断的根据是
!
!
图
&!& ) $
"!
在四边形
#$%&
中!
#&
)
$%
!要判定
#$%&
是平行四边形!那么还需满足 %
!!
&
*!
#
#0
#
%'$2"( ,!
#
$0
#
&'$2"(
.!
#
#0
#
$'$2"( /!
#
#0
#
&'$2"(
!前置巩固"如果你没有全部正确#务必回顾复习
!
利用边的关系进行平行四边形的判定!方法有"
!
两组对边分别平行'
"
两组对边分别相等'
#
一组对边平行且相等
!
!!
我们已经学习了从边的关系来证明一个四边形是平行四边形#那么从角的关系能够
证明吗$ 从对角线的关系呢$
!!
性质与判定可以成对进行辨析
平行四边形的两组对边分别平行!反过来!两组对边分别平行的四边形是平行四边形
!
平行四边形的两组对边分别相等!反过来!两组对边分别相等的四边形是平行四边形
!
"!
对角线互相平分的四边形是平行四边形
由于对角线互相平分且对顶角相等!可证明三角形全等!得到一组对边平行且相等!
从而证明了对角线互相平分的四边形是平行四边形
!
#!
两组对角分别相等的四边形是平行四边形
利用对角相等与四边形内角和等于
+-"(
!得到邻角都互补!从而两组对边分别平行!
证明了两组对角分别相等的四边形是平行四边形
!
!!
下面给出了四边形
#$%&
中
#
#
!
#
$
!
#
%
!
#
&
的度数之比!其中能判定四边形
#$%&
是平行四边形的是 %
!!
&
*!$%&%+%) ,!&%&%+%+
.!&%+%+%& /!&%+%&%+
!
图
&!& ) &
"!
如图
&!& ) &
!在
-
#$%&
中!对角线
#%
!
$&
相交于点
+
!
'
!
(
是对角线
#%
上的两点!当
'
!
(
满足下列哪个条件时!四边
形
&'$(
不一定是平行四边形 %
!!
&
*!#''%( ,!&''$(
.!
#
#&''
#
%$( /!
#
#'&'
#
%($
#!
已知四边形
#$%&
的对角线
#%
!
$&
相交于点
+
!给出下列
!
个条件"
!
#$
)
%&
'
"
+#'+%
'
#
#$'%&
'
$#
$#&'
#
&%$
'
%
#&
)
$%!
从以上
!
个条件中任选
&
个条件!能推出四边形
#$%&
是平行四边形的有"
!
%用序号表示&
!
要理清平行四边形的判定与性质的区别
!
学会从边$角$对角线的关系去判定一个四
边形的形状!同时也会利用平行四边形的性质去得到边$角$对角线的关系
!
!!
能够判定一个四边形是平行四边形的条件是 %
!!
&
*!
一组对角相等
,!
两条对角线互相平分
.!
两条对角线互相垂直
/!
一对邻角的和为
$2"(
"!
如图
&!& ) +
!
'
!
(
是
-
#$%&
对角线
$&
上的两点!请你添加一个适当的条件"
!!!!!
!使四边形
#'%(
是平行四边形
!
图
&!& ) +
#!
如图
&!& ) )
!在
-
#$%&
中!
$2'&0
!
$''&(
!四边形
0'2(
是平行四边形吗#
!
图
&!& ) )
为什么#
!
!
!
!
!
!
! !
"!"
.9:8%
!"
!前置诊断"
!!*
!
"!!
!变式训练"
!!!
"!.
四边形
"$%#
是平行四边形#
1"#
)
$%
#
"#-$%!
.",-%/
#
1#,-$/!
在
#
#',
和
#
$'/
中#
"
#',-
"
$'/
#
"
'#,-
"
'$/
#
#,-$/
#
1
#
#',
(#
$'/!
1',-'/!
!效果检测"
!!"
!
"!,+67
#
'+67
#
,+67
#
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
'+67
!#(
!
#!.
四边形
"$%#
是平行四边形#
1"$
)
#%
#
"$-%#!
.$,-#/
#
1"$8$,-%#8#/
#即
",-%/!
."$
)
#%
#
1",
)
/%
#
1
"
%",-
"
"%/
#
"
,-
"
/
#
1
#
"',
(#
%'/!
1',-'/!
"!"
.9:8%
!
"
"
!前置诊断"
!!!
!
"!*
!变式训练"
!!"
"!#
!
.)67
#
,67
#
967
可以组成三角形#
1
三
角形三边都可以作为对角线#另外两边为平行
四边形的边#这样组成的平行四边形一共
#
个
!
#!',-'/!
理由如下$
在
*
"$%#
中#
."%
#
$#
交于点
'
#
1'$-'#
#
"
'$,-
"
'#/!
又
"
$',-
"
#'/
#
1
#
'$,
(#
'#/!
1',-'/!
!效果检测"
!!!
!
"!&
!
#!'#)%
$!"$-%#-'267
#
"#-$%-''67
%!',-'/!
理由如下$
.
四边形
"$%#
是平行四边形#
1"#-$%
#
"#
)
$%!
又
$,-#/
#
1"/-%,!
又
"
'"/-
"
'%,
#
"
"'/-
"
%',
#
1
#
'"/
(#
'%,
!
&&@
"
!
1',-'/!
"!"
.9:8%
!
#
"
!前置诊断"
!!*
"!!
!
.
四边形
"$%#
为平行四边形#
1"$
)
#%
#
"#
)
$%
#
1
"
1#"-
"
3
#
"
3#%-
"
1!
又
"
3#%-
"
1#"
#
1
"
1#"-
"
3-
"
3#%-
"
1
#
1"1-"#
#
%3-%#
#
$1-$3-3!
1
*
"$%#
的周长
-"$8$%8%#8#"-
"$8$%8%38"1-$18$3-($1-'(!
!变式训练"
!!"#
)
$%
!或者
"$-%#
"
"!.
"
$"%-
"
#%"
#
"
#"%-
"
$%"
#
1"$
)
#%
#
"#
)
$%
#
1
四边形
"$%#
是平行四边形#
1"#-$%!
!效果检测"
!!!
"!
*
"$%#
和
*
%#,/
!
一组对边平行且相等的
四边形是平行四边形
!
两组对边分别相等的四
边形是平行四边形
#!.
四边形
"$%#
是平行四边形#
1+
#
"$%
-+
#
"#%
!
又
.#,
$
"%
#
$/
$
"%
#
1#,-$/
#
#,
)
/$
#
1
四边形
#,$/
为平行四边形
!
"!"
.9:8%
!
$
"
!前置诊断"
!!#
!
两组对边分别相等的四边形是平行四边形
"!!
!变式训练"
!!!
!
"!
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
"
#!
"#
#
"$
#
"%
#
"&
#
#&
#
%&
"#
$
#
"'$
与
#
%'#
全等#从而
"$-%#
#
一组对边平行且相等的四边形是平行四边形(
"$
$一组对边平行且相等的四边形是平行四
边形(
"%
$易证
"
"$%-
"
"#%
#两组对角分别相
等的四边形是平行四边形(
"&
$两组对边分别平行的四边形是平行四
边形(
#&
$
#
"'#
与
#
%'$
全等#从而
"#-%$
#
一组对边平行且相等的四边形是平行四边形(
%&
$易证
"
"$%-
"
"#%
#两组对角分别相
等的四边形是平行四边形
!
!效果检测"
!!"
"!
"
$",-
"
#%/
!或
"
#"/-
"
$%,
或
$,-
#/
或
",
)
/%
或
"/
)
,%
"
#!
四边形
1,3/
是平行四边形
!
理由如下$
.
四边形
"$%#
是平行四边形#
1
"
1#/-
"
3$,!
又
.$3-#1
#
$,-#/
#
1
#
#1/
(#
$3,
!
@&@
"
!
11/-,3
#
"
#/1 -
"
$,3!
1
"
1/,-
"
3,/
#
11/
)
,3
#
1
四边形
1,3/
是 四边形
!
!
!
!
!
!
!
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
!
平行四边形! "
!前置诊断"检测你的基础#助力新课学习
!
!!
已知平行四边形的面积是
$))
!相邻两边上的高分别为
2
和
1
!则它的周长是 %
!!
&
*!$3 ,!+) .!-2 /!3&
"!
用
&"#
长的一铁丝围成一个平行四边形!使长边与短边的比为
+%&
!则短边长为
%
!!
&
*!$&# ,!2# .!-# /!)#
!前置巩固"如果你没有全部正确#务必回顾复习
!
平行四边形的周长为两邻边和的两倍
!
!!
在小学#我们已初步认识了平行四边形#平行四边形究竟具有什么样的性质呢$通过
本节课的学习#我们将更加深入地认识平行四边形
!
!!
平行四边形的定义
两组对边分别平行的四边形叫作平行四边形
!
"!
根据定义画一个平行四边形!测量平行四边形四条边的长度$四个角的大小!你能
做出什么猜测#
%
$
&猜想"通过观察和测量!发现平行四边形对边相等!对角相等'
%
&
&验证猜想
!
如图
&!& $ $
!连接
#%!
!
图
&!& $ $
:
四边形
#$%&
为平行四边形!
;#$
)
&%
!
#&
)
$%
%平行四边形的两组对边分别平行&
!
;
#
$'
#
&
!
#
+'
#
)!
又
#%'%#
!
;
"
#$%
("
%&#!
;#$'%&
!
$%'&#
!
#
$'
#
&!
又
#
$0
#
)'
#
&0
#
+
!
;
#
$#&'
#
&%$!
#!
%
$
&平行四边形边的性质"
对边平行)))平行四边形的定义'
对边相等)))连接对角线!由全等三角形证明
!
%
&
&平行四边形角的性质"
邻角互补)))两直线平行!同旁内角互补'
对角相等)))同角的补角相等!即对角相等
!
!!
如图
&!& $ &
!在
-
#$%&
中!
#$'+
!
$%'!
!
#
#$%
的平分线交
#&
于点
'
!则
&'
的长为 %
!!
&
!
图
&!& $ &
*!
,!)
.!+
/!&
"!
如图
&!& $ +
!在
-
#$%&
中!点
'
!
(
分别在
#&
!
$%
上!且
#''%(
!
'(
!
$&
相交
于点
+!
求证"
+''+(!
图
&!& $ +
$!
平行四边形的内角和为
+-"(
!外角和为
+-"(!
&!
任何一条对角线将平行四边形分成两个全等的三角形
!
+!
平行四边形的性质为证明线段相等$角相等提供了新思路$新方法
!
)!
连接对角线!把四边形转化为两个三角形是解决四边形问题的常用方法
!
!!
如图
&!& $ )
!在
-
#$%&
中!
#
$'2"(
!
#'
平分
#
$#&
交
$%
于点
'
!
%(
)
'#
交
#&
于点
(
!则
#
$
的度数为 %
!!
&
图
&!& $ )
*!)"( ,!"( .!-"( /!2"(
"!
已知平行四边形的周长为
$""8#
!两邻边之差为
+"8#
!求平行四边形各边的长
!
#!
已知"如图
&!& $ !
!在
-
#$%&
中!延长
#$
至点
'
!延长
%&
至点
(
!使得
$''
&(
!连接
'(
!与对角线
#%
交于点
+!
求证"
+''+(!
!
图
&!& $ !
"!"
!
平行四边形!
"
"
!前置诊断"检测你的基础#助力新课学习
!
!!
在
-
#$%&
中!若
#
#'-!(
!则
#
%
的度数是 %
!!
&
*!$"!( ,!$$!( .!$&!( /!-!(
!
图
&!& & $
"!
如图
&!& & $
!四边形
#$%&
为平行四边形!
(
是
%&
的中点!
连接
#(
并延长与
$%
的延长线交于点
'
!则下面的结论不正确
的是 %
!!
&
*!#&'$% ,!#&'%'
.!#&'%( /!$%'%'
!前置巩固"如果你没有全部正确#务必回顾复习
!
平行四边形两组对边分别平行且相等!对角相等
!
!!
我们知道平行四边形的两组对边分别平行且相等#对角相等#那么平行四边形还有
什么其他的性质吗$ 对角线又有怎样的性质呢$
!!
平行四边形的对角线
连接平行四边形不相邻的两顶点得到的线段是平行四边形的对角线!平行四边形有
两条对角线!且相交于一点
!
"!
平行四边形对角线的性质
!
图
&!& & &
如图
&!& & &
!
:
四边形
#$%&
是平行四边形!
;#$
)
&%
!
#$'&%
!
;
#
$'
#
&
!
#
+'
#
)
!
;
"
+#$
("
+%&!
;+#'+%
!
+$'+&!
由此得到平行四边形的对角线互相平分
!
!
图
&!& & +
!!
如图
&!& & +
!
-
#$%&
的对角线
#%
!
$&
相交于点
+
!且
#%0$&'$-
!
%&'-
!则
"
#$+
的周长是 %
!!
&
*!$" ,!$)
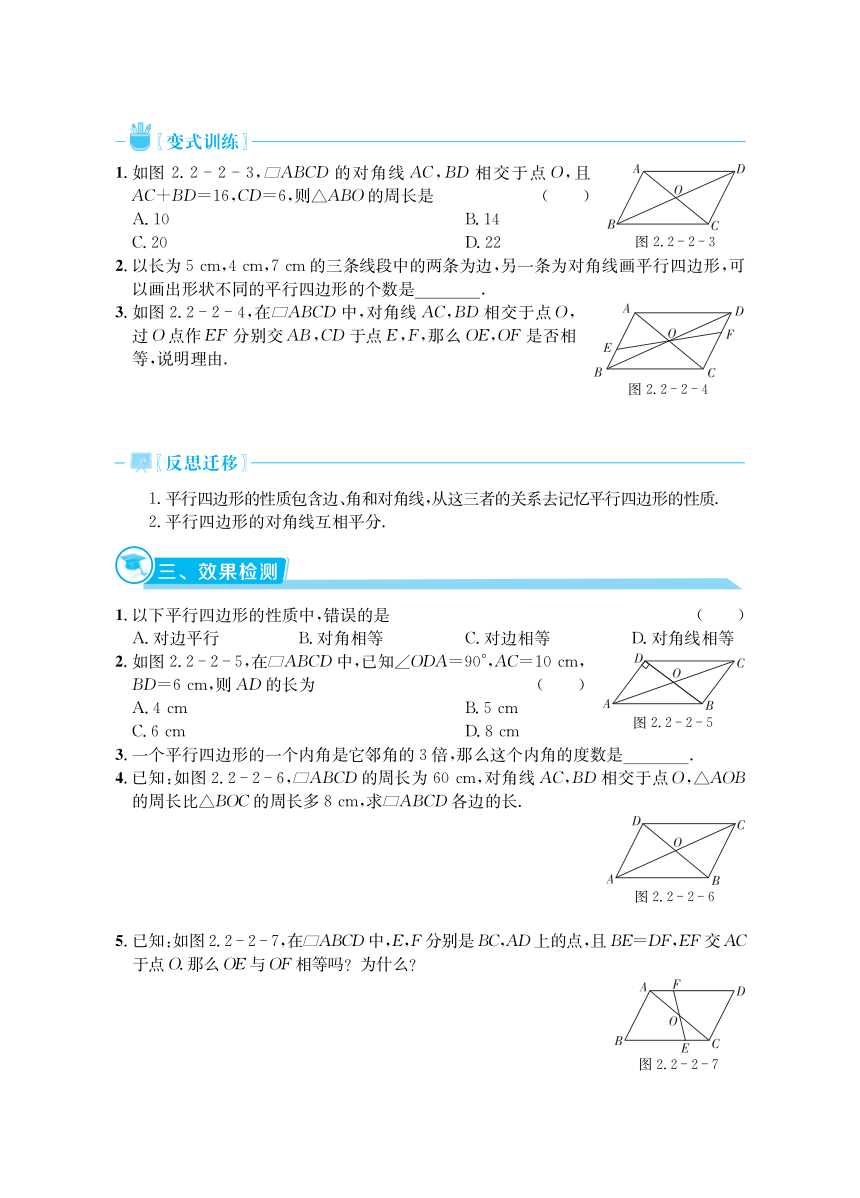
.!&" /!&&
"!
以长为
!8#
!
)8#
!
38#
的三条线段中的两条为边!另一条为对角线画平行四边形!可
以画出形状不同的平行四边形的个数是
!!!!
!
!
图
&!& & )
#!
如图
&!& & )
!在
-
#$%&
中!对角线
#%
!
$&
相交于点
+
!
过
+
点作
'(
分别交
#$
!
%&
于点
'
!
(
!那么
+'
!
+(
是否相
等!说明理由
!
$!
平行四边形的性质包含边$角和对角线!从这三者的关系去记忆平行四边形的性质
!
&!
平行四边形的对角线互相平分
!
!!
以下平行四边形的性质中!错误的是 %
!!
&
*!
对边平行
,!
对角相等
.!
对边相等
/!
对角线相等
!
图
&!& & !
"!
如图
&!& & !
!在
-
#$%&
中!已知
#
+&#'1"(
!
#%'$"8#
!
$&'-8#
!则
#&
的长为 %
!!
&
*!)8# ,!8#
.!-8# /!28#
#!
一个平行四边形的一个内角是它邻角的
+
倍!那么这个内角的度数是
!!!!
!
$!
已知"如图
&!& & -
!
-
#$%&
的周长为
-"8#
!对角线
#%
!
$&
相交于点
+
!
"
#+$
的周长比
"
$+%
的周长多
28#
!求
-
#$%&
各边的长
!
!
图
&!& & -
%!
已知"如图
&!& & 3
!在
-
#$%&
中!
'
!
(
分别是
$%
!
#&
上的点!且
$''&(
!
'(
交
#%
于点
+!
那么
+'
与
+(
相等吗# 为什么#
!
图
&!& & 3
"!"
!
平行四边形!
#
"
!前置诊断"检测你的基础#助力新课学习
!
!!
如图
&!& + $
!
+
是
-
#$%&
对角线的交点!
"
+$%
的周长为
!1
!
$&'+2
!
#%'&)
!
则
#&
的长是 %
!!
&
*!$& ,!$1 .!&2 /!+$
"!
如图
&!& + &
!在
"
0$2
中!
$0'-
!点
#
!
%
!
&
分别在
0$
!
$2
!
02
上!四边形
#$%&
为平行四边形!
#
2&%'
#
0&#
!则
-
#$%&
的周长是 %
!!
&
*!&) ,!$2 .!$- /!$&
图
&!& + $
!!!! 图
&!& + &
!前置巩固"如果你没有全部正确#务必回顾复习
!
平行四边形的性质"
!
两组对边分别平行且相等'
"
平行四边形的对角相等!邻角互补'
#
平行四边形的对角线互相平分
!
!!
我们已经学习了平行四边形的边+角以及对角线的相关性质#那么如何判定一个四
边形是平行四边形呢$ 它的边+角以及对角线又要满足什么条件呢$
!!
定义是判定的基本方法
利用平行四边形的定义可以判定一个四边形是不是平行四边形!即看两组对边是不
是分别平行
!
"!
平行四边形的判定定理
两组对边分别相等的四边形是平行四边形
!
只要连接对角线!利用全等!得到内错角
相等!从而证明两组对边分别平行
!
一组对边平行且相等的四边形是平行四边形
!
连接对角线!利用全等!得到另一组对
边也平行
!
!!
已知
#&'$%
!要使四边形
#$%&
是平行四边形!还需补充的一个条件是"
!!!!
!
"!
如图
&!& + +
!已知
#%
是四边形
#$%&
的对角线!
#
$#%'
#
&%#
!
#
&#%'
#
$%#
!求证"
#&'$%!
!
图
&!& + +
平行四边形的判定从边的关系来看!定义是基础!结合全等可以得到判定定理
$
和
&
!特别是一组对边平行且相等是常用的方法
!
!!
下列条件中!不能够判定一个四边形是平行四边形的是 %
!!
&
*!
两组对边分别相等
,!
两组对边分别平行
.!
一组对边平行且相等
/!
一组对边平行!另一组对边相等
"!
如图
&!& + )
!
#$
与
&%
平行且相等!
&%''('$"
!
&''%('2
!则图中的平行四
边形有
!!!!!!!!!!
!理由分别是
!!!!!!!!!!!
$
!!!!!!
!!!!!
!
图
&!& + )
#!
如图
&!& + !
!在
-
#$%&
中!
&'
$
#%
!
$(
$
#%
!证明"四边形
&'$(
为平行四
边形
!
!
图
&!& + !
"!"
!
平行四边形!
$
"
!前置诊断"检测你的基础#助力新课学习
!
!!
九根火柴棒排成如图
&!& ) $
形状!图中有
! !
个平行四边形!你判断的根据是
!
!
图
&!& ) $
"!
在四边形
#$%&
中!
#&
)
$%
!要判定
#$%&
是平行四边形!那么还需满足 %
!!
&
*!
#
#0
#
%'$2"( ,!
#
$0
#
&'$2"(
.!
#
#0
#
$'$2"( /!
#
#0
#
&'$2"(
!前置巩固"如果你没有全部正确#务必回顾复习
!
利用边的关系进行平行四边形的判定!方法有"
!
两组对边分别平行'
"
两组对边分别相等'
#
一组对边平行且相等
!
!!
我们已经学习了从边的关系来证明一个四边形是平行四边形#那么从角的关系能够
证明吗$ 从对角线的关系呢$
!!
性质与判定可以成对进行辨析
平行四边形的两组对边分别平行!反过来!两组对边分别平行的四边形是平行四边形
!
平行四边形的两组对边分别相等!反过来!两组对边分别相等的四边形是平行四边形
!
"!
对角线互相平分的四边形是平行四边形
由于对角线互相平分且对顶角相等!可证明三角形全等!得到一组对边平行且相等!
从而证明了对角线互相平分的四边形是平行四边形
!
#!
两组对角分别相等的四边形是平行四边形
利用对角相等与四边形内角和等于
+-"(
!得到邻角都互补!从而两组对边分别平行!
证明了两组对角分别相等的四边形是平行四边形
!
!!
下面给出了四边形
#$%&
中
#
#
!
#
$
!
#
%
!
#
&
的度数之比!其中能判定四边形
#$%&
是平行四边形的是 %
!!
&
*!$%&%+%) ,!&%&%+%+
.!&%+%+%& /!&%+%&%+
!
图
&!& ) &
"!
如图
&!& ) &
!在
-
#$%&
中!对角线
#%
!
$&
相交于点
+
!
'
!
(
是对角线
#%
上的两点!当
'
!
(
满足下列哪个条件时!四边
形
&'$(
不一定是平行四边形 %
!!
&
*!#''%( ,!&''$(
.!
#
#&''
#
%$( /!
#
#'&'
#
%($
#!
已知四边形
#$%&
的对角线
#%
!
$&
相交于点
+
!给出下列
!
个条件"
!
#$
)
%&
'
"
+#'+%
'
#
#$'%&
'
$#
$#&'
#
&%$
'
%
#&
)
$%!
从以上
!
个条件中任选
&
个条件!能推出四边形
#$%&
是平行四边形的有"
!
%用序号表示&
!
要理清平行四边形的判定与性质的区别
!
学会从边$角$对角线的关系去判定一个四
边形的形状!同时也会利用平行四边形的性质去得到边$角$对角线的关系
!
!!
能够判定一个四边形是平行四边形的条件是 %
!!
&
*!
一组对角相等
,!
两条对角线互相平分
.!
两条对角线互相垂直
/!
一对邻角的和为
$2"(
"!
如图
&!& ) +
!
'
!
(
是
-
#$%&
对角线
$&
上的两点!请你添加一个适当的条件"
!!!!!
!使四边形
#'%(
是平行四边形
!
图
&!& ) +
#!
如图
&!& ) )
!在
-
#$%&
中!
$2'&0
!
$''&(
!四边形
0'2(
是平行四边形吗#
!
图
&!& ) )
为什么#
!
!
!
!
!
!
! !
"!"
.9:8%
!"
!前置诊断"
!!*
!
"!!
!变式训练"
!!!
"!.
四边形
"$%#
是平行四边形#
1"#
)
$%
#
"#-$%!
.",-%/
#
1#,-$/!
在
#
#',
和
#
$'/
中#
"
#',-
"
$'/
#
"
'#,-
"
'$/
#
#,-$/
#
1
#
#',
(#
$'/!
1',-'/!
!效果检测"
!!"
!
"!,+67
#
'+67
#
,+67
#
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
'+67
!#(
!
#!.
四边形
"$%#
是平行四边形#
1"$
)
#%
#
"$-%#!
.$,-#/
#
1"$8$,-%#8#/
#即
",-%/!
."$
)
#%
#
1",
)
/%
#
1
"
%",-
"
"%/
#
"
,-
"
/
#
1
#
"',
(#
%'/!
1',-'/!
"!"
.9:8%
!
"
"
!前置诊断"
!!!
!
"!*
!变式训练"
!!"
"!#
!
.)67
#
,67
#
967
可以组成三角形#
1
三
角形三边都可以作为对角线#另外两边为平行
四边形的边#这样组成的平行四边形一共
#
个
!
#!',-'/!
理由如下$
在
*
"$%#
中#
."%
#
$#
交于点
'
#
1'$-'#
#
"
'$,-
"
'#/!
又
"
$',-
"
#'/
#
1
#
'$,
(#
'#/!
1',-'/!
!效果检测"
!!!
!
"!&
!
#!'#)%
$!"$-%#-'267
#
"#-$%-''67
%!',-'/!
理由如下$
.
四边形
"$%#
是平行四边形#
1"#-$%
#
"#
)
$%!
又
$,-#/
#
1"/-%,!
又
"
'"/-
"
'%,
#
"
"'/-
"
%',
#
1
#
'"/
(#
'%,
!
&&@
"
!
1',-'/!
"!"
.9:8%
!
#
"
!前置诊断"
!!*
"!!
!
.
四边形
"$%#
为平行四边形#
1"$
)
#%
#
"#
)
$%
#
1
"
1#"-
"
3
#
"
3#%-
"
1!
又
"
3#%-
"
1#"
#
1
"
1#"-
"
3-
"
3#%-
"
1
#
1"1-"#
#
%3-%#
#
$1-$3-3!
1
*
"$%#
的周长
-"$8$%8%#8#"-
"$8$%8%38"1-$18$3-($1-'(!
!变式训练"
!!"#
)
$%
!或者
"$-%#
"
"!.
"
$"%-
"
#%"
#
"
#"%-
"
$%"
#
1"$
)
#%
#
"#
)
$%
#
1
四边形
"$%#
是平行四边形#
1"#-$%!
!效果检测"
!!!
"!
*
"$%#
和
*
%#,/
!
一组对边平行且相等的
四边形是平行四边形
!
两组对边分别相等的四
边形是平行四边形
#!.
四边形
"$%#
是平行四边形#
1+
#
"$%
-+
#
"#%
!
又
.#,
$
"%
#
$/
$
"%
#
1#,-$/
#
#,
)
/$
#
1
四边形
#,$/
为平行四边形
!
"!"
.9:8%
!
$
"
!前置诊断"
!!#
!
两组对边分别相等的四边形是平行四边形
"!!
!变式训练"
!!!
!
"!
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
"
#!
"#
#
"$
#
"%
#
"&
#
#&
#
%&
"#
$
#
"'$
与
#
%'#
全等#从而
"$-%#
#
一组对边平行且相等的四边形是平行四边形(
"$
$一组对边平行且相等的四边形是平行四
边形(
"%
$易证
"
"$%-
"
"#%
#两组对角分别相
等的四边形是平行四边形(
"&
$两组对边分别平行的四边形是平行四
边形(
#&
$
#
"'#
与
#
%'$
全等#从而
"#-%$
#
一组对边平行且相等的四边形是平行四边形(
%&
$易证
"
"$%-
"
"#%
#两组对角分别相
等的四边形是平行四边形
!
!效果检测"
!!"
"!
"
$",-
"
#%/
!或
"
#"/-
"
$%,
或
$,-
#/
或
",
)
/%
或
"/
)
,%
"
#!
四边形
1,3/
是平行四边形
!
理由如下$
.
四边形
"$%#
是平行四边形#
1
"
1#/-
"
3$,!
又
.$3-#1
#
$,-#/
#
1
#
#1/
(#
$3,
!
@&@
"
!
11/-,3
#
"
#/1 -
"
$,3!
1
"
1/,-
"
3,/
#
11/
)
,3
#
1
四边形
1,3/
是 四边形
!
!
!
!
!
!
!
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
&
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
