人教版六年级下册4.2.1正比例和反比例——正比例课件(16张PPT)
文档属性
| 名称 | 人教版六年级下册4.2.1正比例和反比例——正比例课件(16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-18 14:24:53 | ||
图片预览





文档简介
(共16张PPT)
4.2.1正比例和反比例
——正比例
人教版 六年级下
新知导入
1、一辆汽车从甲地开往乙地,10分钟总共行驶了120千米,它每分钟行驶多少千米?
120÷10=12(千米)
答:它每分钟行驶12千米。
①已知路程和时间,可以求速度?
速度 = 路程÷时间
2、妈妈在商店买了12支笔,一共24元,每支笔多少元?
24÷12=2(元)
答:每支笔2元。
②已知总价和数量,可以求单价?
单价 = 总价÷数量
③已知工作总量和工作时间,怎样求工作效率?
工作效率 = 工作总量÷工作时间
这节课我们一起来研究有特殊关系的两种相关联的量。
新知讲解
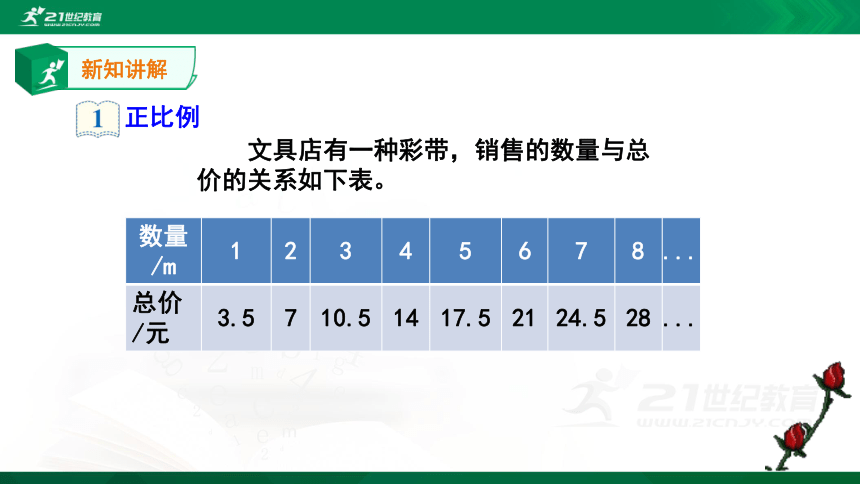
文具店有一种彩带,销售的数量与总价的关系如下表。
数量/m 1 2 3 4 5 6 7 8 ...
总价
/元 3.5 7 10.5 14 17.5 21 24.5 28 ...
正比例
新知讲解
观察上表,回答下面的问题:
(1)表中有哪两个量? (2)总价是怎样随着数量变化的?
(3)相对应的总价和数量的比是多少?比值是多少?
数量/m 1 2 3 4 5 6 7 8 ...
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 ...
通过观察上表可知:(1)有数量和总价两种相关联的量。
(2)数量增加,总价增加;数量减少,总价也减少。
(3)总价和数量的比分别为:
=
=
=
=
=
=
=
=
=
3.5
比值为:
新知讲解
比值3.5,实际就是彩带的单价。用式子表示它们的关系就是:
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
如果用字母y和x表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用下面的式子表示:
新知讲解
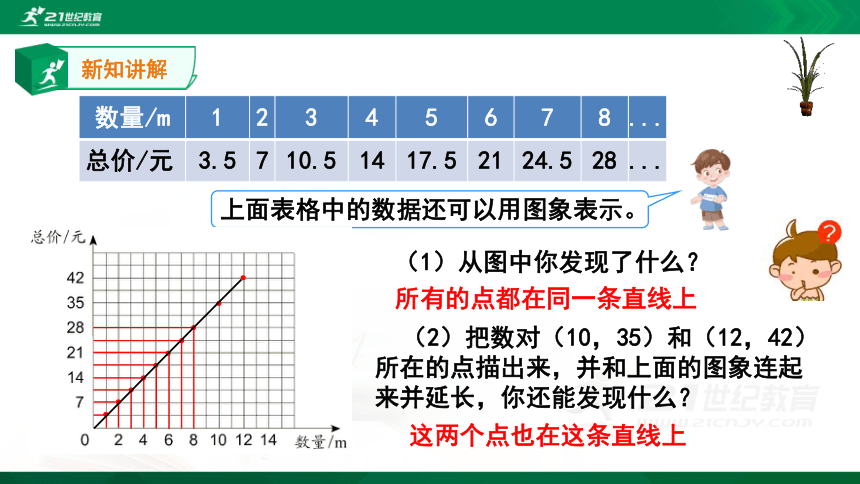
上面表格中的数据还可以用图象表示。
数量/m 1 2 3 4 5 6 7 8 ...
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 ...
(1)从图中你发现了什么?
(2)把数对(10,35)和(12,42)所在的点描出来,并和上面的图象连起来并延长,你还能发现什么?
所有的点都在同一条直线上
这两个点也在这条直线上
新知讲解
(3)不计算,根据图像判断,如果买9m彩带,总价是多少?49元能买多少米彩带?
(9,31.5)
(14,49)
买9m彩带总价31.5元;
49元能买14m彩带。
由 可知:
(4)小明买的彩带的米数是小丽的2倍,他花的钱是小丽的几倍?
他花的钱也是小丽的2倍。
你能举出生活中正比例关系的例子吗?
如:正方形的周长与边长成正比例关系。
课堂练习
做一做
1、一辆汽车行驶的时间和路程如下表。
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
(1)写出几组路程与相对的时间的比,并比较比值的大小。
=
=
=
=
=
=
80
(2)说一说这个比值表示什么。
这个比值表示汽车行驶的速度。
(3)汽车行驶的路程与时间成正比例关系吗?为什么?
成正比例;因为路程和时间对应的比值一定,都等于80。
课堂练习
(4)在图中描出表示路程和相对应时间的点,然后把它们按顺序连接起来。并估计一下行驶120km大约要用多少时间。
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
120
1.5
行驶120km大约需要1.5小时
120÷80=1.5(千米)
(7)和一定,加数和另一个加数成正比例。( )
(4)圆的半径和周长成正比例。( )
课堂练习
(2)长方形的长一定,宽与面积成正比例。( )
(1)一个因数不变,积与另一个因数成正比例。 ( )
(3)大米的总量一定,吃掉的和剩下的成正比列。( )
1、判断对错。
×
√
(5)分数的分子一定,分数值和分母成正比列。( )
×
×
√
√
(6)如果3m=8n,那么m与n成正比列。( )
√
课堂练习
2、一房间铺地面积和用砖块数如下表。
铺地面积(m2) 1 2 3 4 5
用砖块数 25 50 75 100 125
(1)表中( )和( )是相关联的量,( )随着( )的变化而变化。
铺地面积
用砖块数
铺地面积
用砖块数
(2)表中第三组这两种量相对应的两个数的比是( ),比值是( );第五组这两种量相对应的两个数的比是( ),比值是( )。
3:75
1
25
5:125
1
25
(3)上面所求出的比值所表示的意义是( ),铺地面积和用砖块数的( )是一定的,所以铺地面积和用砖块数( )。
每块地砖面积
比值
成正比列
课堂练习
3、下面是水果批发市场苹果、橘子销售价格的图像,请根据图像计算并填空。
(1)两种水果中,较贵的是( )。
(2)苹果和橘子各买5千克,一共需要( )元。
(3)用36元可以购买橘子的数量与可以购买苹果的数量的比是( )。
橘子
75
2:3
课堂总结
相关联的两种量y和x,如果它们的比值k一定,则y和x叫做成正比例的量,它们的关系叫做正比例关系。
正比例
正比例关系表达式:
正比例图像
画法:
运用:
表格
描点
连线
求值
找点
直线
作业布置
1、完成书上第49-50页,第1-7题的作业。
2、探究生活中成正比例的量的实际应用。
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
4.2.1正比例和反比例
——正比例
人教版 六年级下
新知导入
1、一辆汽车从甲地开往乙地,10分钟总共行驶了120千米,它每分钟行驶多少千米?
120÷10=12(千米)
答:它每分钟行驶12千米。
①已知路程和时间,可以求速度?
速度 = 路程÷时间
2、妈妈在商店买了12支笔,一共24元,每支笔多少元?
24÷12=2(元)
答:每支笔2元。
②已知总价和数量,可以求单价?
单价 = 总价÷数量
③已知工作总量和工作时间,怎样求工作效率?
工作效率 = 工作总量÷工作时间
这节课我们一起来研究有特殊关系的两种相关联的量。
新知讲解
文具店有一种彩带,销售的数量与总价的关系如下表。
数量/m 1 2 3 4 5 6 7 8 ...
总价
/元 3.5 7 10.5 14 17.5 21 24.5 28 ...
正比例
新知讲解
观察上表,回答下面的问题:
(1)表中有哪两个量? (2)总价是怎样随着数量变化的?
(3)相对应的总价和数量的比是多少?比值是多少?
数量/m 1 2 3 4 5 6 7 8 ...
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 ...
通过观察上表可知:(1)有数量和总价两种相关联的量。
(2)数量增加,总价增加;数量减少,总价也减少。
(3)总价和数量的比分别为:
=
=
=
=
=
=
=
=
=
3.5
比值为:
新知讲解
比值3.5,实际就是彩带的单价。用式子表示它们的关系就是:
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
如果用字母y和x表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以用下面的式子表示:
新知讲解
上面表格中的数据还可以用图象表示。
数量/m 1 2 3 4 5 6 7 8 ...
总价/元 3.5 7 10.5 14 17.5 21 24.5 28 ...
(1)从图中你发现了什么?
(2)把数对(10,35)和(12,42)所在的点描出来,并和上面的图象连起来并延长,你还能发现什么?
所有的点都在同一条直线上
这两个点也在这条直线上
新知讲解
(3)不计算,根据图像判断,如果买9m彩带,总价是多少?49元能买多少米彩带?
(9,31.5)
(14,49)
买9m彩带总价31.5元;
49元能买14m彩带。
由 可知:
(4)小明买的彩带的米数是小丽的2倍,他花的钱是小丽的几倍?
他花的钱也是小丽的2倍。
你能举出生活中正比例关系的例子吗?
如:正方形的周长与边长成正比例关系。
课堂练习
做一做
1、一辆汽车行驶的时间和路程如下表。
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
(1)写出几组路程与相对的时间的比,并比较比值的大小。
=
=
=
=
=
=
80
(2)说一说这个比值表示什么。
这个比值表示汽车行驶的速度。
(3)汽车行驶的路程与时间成正比例关系吗?为什么?
成正比例;因为路程和时间对应的比值一定,都等于80。
课堂练习
(4)在图中描出表示路程和相对应时间的点,然后把它们按顺序连接起来。并估计一下行驶120km大约要用多少时间。
时间/时 1 2 3 4 5 6
路程/km 80 160 240 320 400 480
120
1.5
行驶120km大约需要1.5小时
120÷80=1.5(千米)
(7)和一定,加数和另一个加数成正比例。( )
(4)圆的半径和周长成正比例。( )
课堂练习
(2)长方形的长一定,宽与面积成正比例。( )
(1)一个因数不变,积与另一个因数成正比例。 ( )
(3)大米的总量一定,吃掉的和剩下的成正比列。( )
1、判断对错。
×
√
(5)分数的分子一定,分数值和分母成正比列。( )
×
×
√
√
(6)如果3m=8n,那么m与n成正比列。( )
√
课堂练习
2、一房间铺地面积和用砖块数如下表。
铺地面积(m2) 1 2 3 4 5
用砖块数 25 50 75 100 125
(1)表中( )和( )是相关联的量,( )随着( )的变化而变化。
铺地面积
用砖块数
铺地面积
用砖块数
(2)表中第三组这两种量相对应的两个数的比是( ),比值是( );第五组这两种量相对应的两个数的比是( ),比值是( )。
3:75
1
25
5:125
1
25
(3)上面所求出的比值所表示的意义是( ),铺地面积和用砖块数的( )是一定的,所以铺地面积和用砖块数( )。
每块地砖面积
比值
成正比列
课堂练习
3、下面是水果批发市场苹果、橘子销售价格的图像,请根据图像计算并填空。
(1)两种水果中,较贵的是( )。
(2)苹果和橘子各买5千克,一共需要( )元。
(3)用36元可以购买橘子的数量与可以购买苹果的数量的比是( )。
橘子
75
2:3
课堂总结
相关联的两种量y和x,如果它们的比值k一定,则y和x叫做成正比例的量,它们的关系叫做正比例关系。
正比例
正比例关系表达式:
正比例图像
画法:
运用:
表格
描点
连线
求值
找点
直线
作业布置
1、完成书上第49-50页,第1-7题的作业。
2、探究生活中成正比例的量的实际应用。
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
