2018-2019学年上海市闵行区二十一校联考七年级第二学期期中数学试卷 含解析
文档属性
| 名称 | 2018-2019学年上海市闵行区二十一校联考七年级第二学期期中数学试卷 含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 16:46:52 | ||
图片预览



文档简介
2018-2019学年七年级第二学期期中数学试卷
一、选择题
1.在,,2.00010001000,,0,0.13,中有理数的个数
A.2个 B.3个 C.4个 D.5个
2.下列说法不正确的是
A.实数包括正实数、零、负实数 B.正整数和负整数统称为整数
C.无理数一定是无限小数 D.2是4的平方根
3.下列计算中正确的是
A. B. C. D.
4.如图:,,,下列条件能得到的是
A. B. C. D.
5.如图:,垂直于,垂足为,,则等于
A. B. C. D.
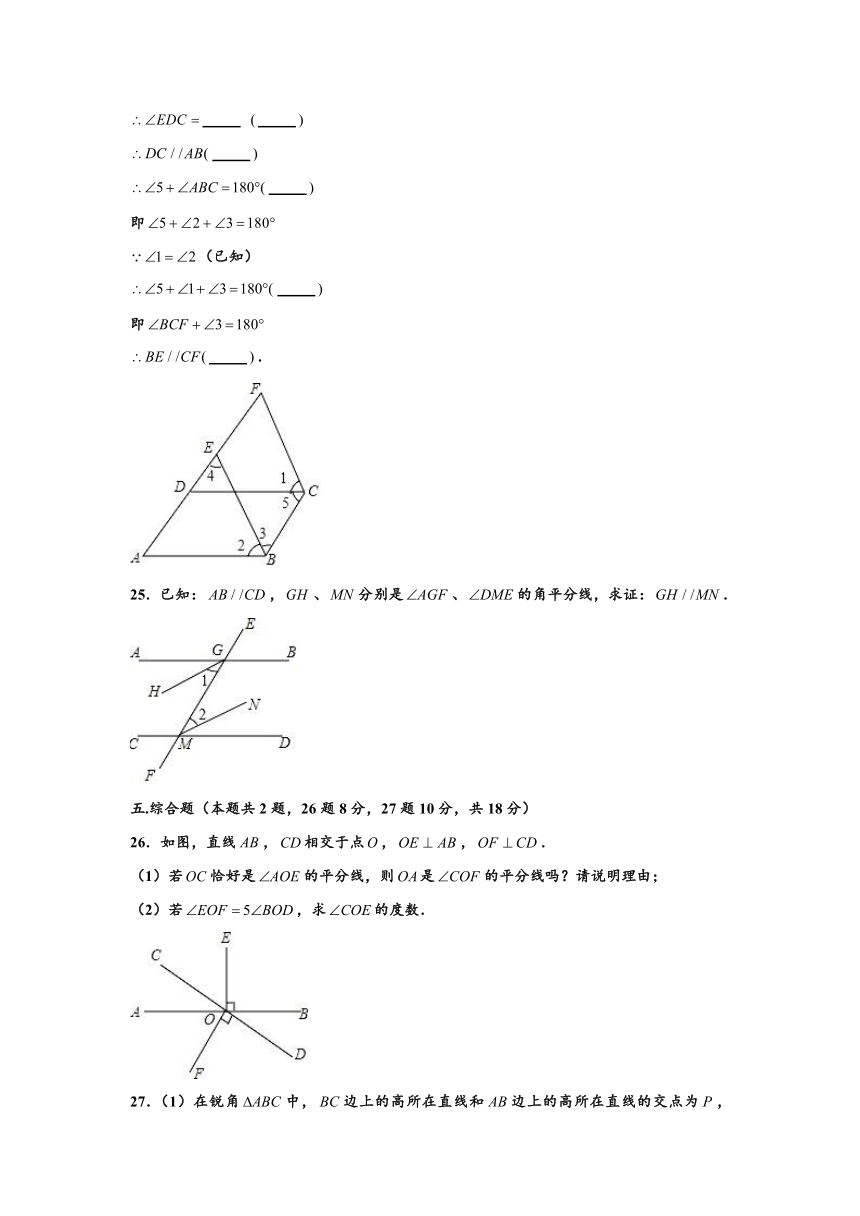
6.如图,同位角共有 对.
A.6 B.5 C.8 D.7
二.填空题(本题共12题,毎题3分,共36分)
7.的平方根是 .
8.计算: .
9.比较大小: (填“”或“” .
10.把化为幂的形式是 .
11.2018年12月,华为轮值董事长郭平在新年致辞中指出“困难越大,荣耀也越大”.2018年公司预计实现销售收入1085亿美元,同比增长.请将1085亿保留三位有效数字为 .
12.把一个长方形纸片按照如图所示的长方形折叠后,的对应点,的对应点,若得到,则 .
13.如果,那么整数 .
14.如果实数与在数轴上分别表示点和点,则线段的距离是 .
15.一个等腰三角形的两边长分别为3和7,这个三角形的周长是 .
16.如图:直线,相交于点,若,则直线与的夹角度数为 .
17.如图,已知,,,则 .
18.如图,对面积为1的逐次进行以下操作:第一次操作,分别延长、、至点、、,使得、、,顺次连接、、,得到△,记其面积为;第二次操作,分别延长、、至点、、,使得、、,顺次连接、、,得到△,记其面积为;;按此规律继续下去,可得到△,则其面积 .
三.简答题(本题共4题,每题4分,共16分)
19.计算:
20.计算:
21.利用幂的运算性质进行计算:
22.解方程:
四.简答题(本题共3题,23题4分,24题7分,25题7分,共18分)
23.作图:如图已知.
(1)作出点到直线的距离;
(2)作出点到直线的距离;
(3)已知,,那么 .
24.如图,已知,,,试说明:.
完善下面的解答过程,并填写理由或数学式:解:
(已知)
(已知)
即
(已知)
即
.
25.已知:,、分别是、的角平分线,求证:.
五.综合题(本题共2题,26题8分,27题10分,共18分)
26.如图,直线,相交于点,,.
(1)若恰好是的平分线,则是的平分线吗?请说明理由;
(2)若,求的度数.
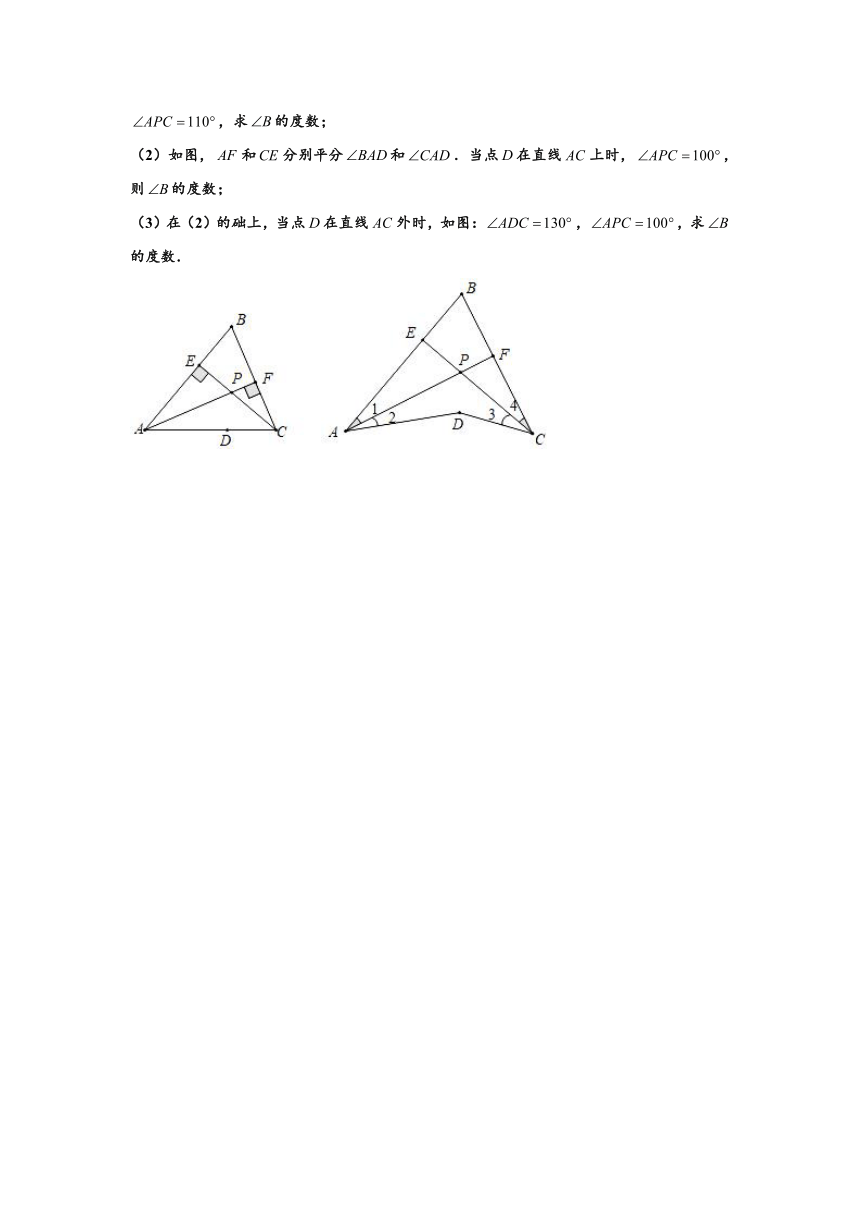
27.(1)在锐角中,边上的高所在直线和边上的高所在直线的交点为,,求的度数;
(2)如图,和分别平分和.当点在直线上时,,则的度数;
(3)在(2)的础上,当点在直线外时,如图:,,求的度数.
参考答案
一、单项选择题(本题共6题,每题2分,共12分)
1.在,,2.00010001000,,0,0.13,中有理数的个数
A.2个 B.3个 C.4个 D.5个
解:在,,2.00010001000,,0,0.13,中,有理数是,2.00010001000,,0,0.13,共有5个.
故选:.
2.下列说法不正确的是
A.实数包括正实数、零、负实数 B.正整数和负整数统称为整数
C.无理数一定是无限小数 D.2是4的平方根
解:、实数包括正实数、零、负实数,正确;
、正整数、0和负整数统称为整数,错误;
、无理数一定是无限小数,正确;
、2是4的平方根,正确;
故选:.
3.下列计算中正确的是
A. B. C. D.
解:,所以错误;
所以错误;
,所以错误;
故选:.
4.如图:,,,下列条件能得到的是
A. B. C. D.
解:,,,
欲使,
则,或.
故选:.
5.如图:,垂直于,垂足为,,则等于
A. B. C. D.
解:垂直于,垂足为,
,
,
.
,
.
故选:.
6.如图,同位角共有 对.
A.6 B.5 C.8 D.7
解:同位角有6对,与,与,与,与,与,与,
故选:.
二.填空题(本题共12题,毎题3分,共36分)
7.的平方根是 .
解:,
的平方根是.
故答案为:.
8.计算: .
解:
故答案为:.
9.比较大小: (填“”或“” .
解:,,
,
故答案为:.
10.把化为幂的形式是 .
解:
故答案为:
11.2018年12月,华为轮值董事长郭平在新年致辞中指出“困难越大,荣耀也越大”.2018年公司预计实现销售收入1085亿美元,同比增长.请将1085亿保留三位有效数字为 .
解:1085亿保留三位有效数字为.
故答案为.
12.把一个长方形纸片按照如图所示的长方形折叠后,的对应点,的对应点,若得到,则 .
解:,
,
,
,
四边形是矩形,
,
.
故答案为:.
13.如果,那么整数 3 .
解:,
,
,
整数.
故答案为:3
14.如果实数与在数轴上分别表示点和点,则线段的距离是 .
解:由题意,得.
故答案是:.
15.一个等腰三角形的两边长分别为3和7,这个三角形的周长是 17 .
解:(1)若3为腰长,7为底边长,
由于,则三角形不存在;
(2)若7为腰长,则符合三角形的两边之和大于第三边.
所以这个三角形的周长为.
故答案为:17.
16.如图:直线,相交于点,若,则直线与的夹角度数为 .
解:,
又,
,
解得.
故直线与的夹角度数为.
故答案为:.
17.如图,已知,,,则 .
解:如图.
,
,
又,
.
故答案是:.
18.如图,对面积为1的逐次进行以下操作:第一次操作,分别延长、、至点、、,使得、、,顺次连接、、,得到△,记其面积为;第二次操作,分别延长、、至点、、,使得、、,顺次连接、、,得到△,记其面积为;;按此规律继续下去,可得到△,则其面积 361 .
解:连接,根据,得到:,
因而若过点,作与△的边上的高,则高线的比是,
因而面积的比是,则△的面积是的面积的2倍,
设的面积是,则△的面积是,
同理可以得到△的面积是△面积的2倍,是,
则△的面积是,
同理△和△的面积都是,
△的面积是,
即△的面积是的面积的19倍,
同理△的面积是△的面积的19倍,
即的面积是19,的面积,
故答案为361.
三.简答题(本题共4题,每题4分,共16分)
19.计算:
解:原式
.
20.计算:
解:原式
.
21.利用幂的运算性质进行计算:
解:
.
22.解方程:
解:,
,
则,
.
四.简答题(本题共3题,23题4分,24题7分,25题7分,共18分)
23.作图:如图已知.
(1)作出点到直线的距离;
(2)作出点到直线的距离;
(3)已知,,那么 6 .
解:(1)线段如图所示.
(2)线段如图所示.
(3),
,
.
故答案为6.
24.如图,已知,,,试说明:.
完善下面的解答过程,并填写理由或数学式:解:
(已知)
(已知)
即
(已知)
即
.
解:
(已知)
内错角相等,两直线平行)
两直线平行,内错角相等)
(已知)
(等量代换)
同位角相等,两直线平行)
(两直线平行,同旁内角互补)
即
(已知)
(等量代换)
即
(同旁内角互补,两直线平行);
故答案为:;内错角相等,两直线平行;两直线平行,内错角相等;;等量代换;同位角相等,两直线平行;两直线平行,同旁内角互补;等量代换;同旁内角互补,两直线平行.
25.已知:,、分别是、的角平分线,求证:.
【解答】证明:,
,
又、分别是、的角平分线,
,,
,
.
五.综合题(本题共2题,26题8分,27题10分,共18分)
26.如图,直线,相交于点,,.
(1)若恰好是的平分线,则是的平分线吗?请说明理由;
(2)若,求的度数.
解:(1)是的平分线.
,
,
恰好是的平分线,
,
,
,
,
是的平分线;
(2)设,
,
,
,
,
,
,
解得,
.
27.(1)在锐角中,边上的高所在直线和边上的高所在直线的交点为,,求的度数;
(2)如图,和分别平分和.当点在直线上时,,则的度数;
(3)在(2)的础上,当点在直线外时,如图:,,求的度数.
解:(1)如图1中,
,是高,
,
,
,
.
(2)如图2中,
,
,
,,
,
.
(3)如图3中,
,,,,
.
同课章节目录
