人教版七年级数学下册课件:5.3.1 平行线的性质(共24张PPT)
文档属性
| 名称 | 人教版七年级数学下册课件:5.3.1 平行线的性质(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 331.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-18 08:45:11 | ||
图片预览








文档简介
课件24张PPT。5.3.1 平行线的性质
知识与技能:理解平行线的性质;
过程与方法:经历平行线性质的探究过程,从中体会研究几何图形的一般方法;
情感态度价值观:形成热爱数学的情感体会数学学科的逻辑严密性。
学习重难点
得到平行线的性质的推理过程.学习目标 判定方法1 同位角相等,两直线平行. 判定方法2 内错角相等,两直线平行.判定方法3 同旁内角互补,两直线平行.1.梳理旧知,引出新课结论 平行线的判定两
直
线
平
行1.梳理旧知,引出新课条件结论?两条平行线
被第三条直
线所截1.梳理旧知,引出新课条件结论同位角?内错角?同旁内角? 探究1:动手操作
(1)利用直尺和三角板画两条平行线a//b;
(2)一条截线c与这两条平行线相交;
(3)度量所形成的八个角
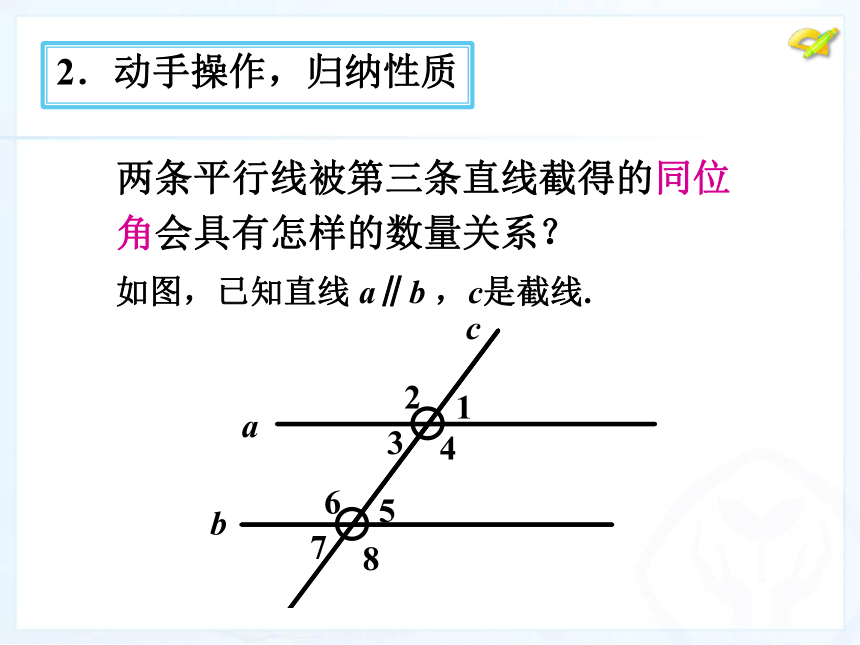
你测到的同位角相等吗? 2.动手操作,归纳性质 两条平行线被第三条直线截得的同位角会具有怎样的数量关系? 2.动手操作,归纳性质 如图,已知直线 a∥b ,c是截线. 两条平行线被第三条直线截得的同位角会具有怎样的数量关系? 2.动手操作,归纳性质性质1 两条平行线被第三条直线 所截,同位角相等. 2.动手操作,归纳性质性质1 两条平行线被第三条直线 所截,同位角相等. 两直线平行,同位角相等的应用 3.应用转化,推出性质 3.应用转化,推出性质性质2 两条平行线被第三条直线 所截,内错角相等.两条平行线被第三条直线截得的内错角会具有怎样的数量关系? 3.应用转化,推出性质性质2 两条平行线被第三条直线 所截,内错角相等. 3.应用转化,推出性质 3.应用转化,推出性质性质3 两条平行线被第三条直线 所截,同旁内角互补.两条平行线被第三条直线截得的同旁内角会具有怎样的数量关系? 3.应用转化,推出性质性质3 两条平行线被第三条直线 所截,同旁内角互补.(1)从∠1=110o.可以知道∠2是多少度吗?为什么?4.巩固新知,深化理解答:∠2 =110o.因为AB∥CD,∠1和∠2是内错角,根据两直线平行,内错角相等,得到∠1=∠2.因为∠1=110o,所以∠2 =110o.例1 如图,平行线AB,CD被直线AE所截.(2)从∠1=110o可以知道∠3是多少度吗?为什么?4.巩固新知,深化理解例1 如图,平行线AB,CD被直线AE所截.答:∠3 =110o.因为AB∥CD ,∠1和∠3是同位角,根据两直线平行,同位角相等,得到∠1=∠3.因为∠1=110o,所以∠3 =110o.(3)从∠1=110o可以知道∠4是多少度吗?为什么?4.巩固新知,深化理解例1 如图,平行线AB,CD被直线AE所截.答:∠4=70o.因为AB∥CD , ∠1和∠4是同旁内角,根据两直线平行,同旁内角互补,得到∠1+∠4=180o.因为∠1=110o,所以∠4=70o.例2 如图,已知AB∥CD,AE∥CF,∠A= 39°,
∠C是多少度?为什么? 4.巩固新知,深化理解方法一
解:∵AB∥CD,
∴ ∠C=∠1.
∵ AE∥CF,
∴ ∠A=∠1.
∴ ∠C=∠A.
∵∠A= 39o,
∴∠C= 39o.4.巩固新知,深化理解1方法二
解:∵AB∥CD,
∴ ∠C=∠2.
∵ AE∥CF,
∴ ∠A=∠2.
∴ ∠C=∠A.
∵∠A= 39o,
∴∠C= 39o.4.巩固新知,深化理解2(1)平行线的性质是什么?5.归纳小结(2)你能用自己的语言叙述研究平行线性质的过程吗? (3)性质2和性质3是通过简单推理得到的,在推理论证中需要注意哪些问题?教科书 习题5.3 第2、4、6题6.布置作业
知识与技能:理解平行线的性质;
过程与方法:经历平行线性质的探究过程,从中体会研究几何图形的一般方法;
情感态度价值观:形成热爱数学的情感体会数学学科的逻辑严密性。
学习重难点
得到平行线的性质的推理过程.学习目标 判定方法1 同位角相等,两直线平行. 判定方法2 内错角相等,两直线平行.判定方法3 同旁内角互补,两直线平行.1.梳理旧知,引出新课结论 平行线的判定两
直
线
平
行1.梳理旧知,引出新课条件结论?两条平行线
被第三条直
线所截1.梳理旧知,引出新课条件结论同位角?内错角?同旁内角? 探究1:动手操作
(1)利用直尺和三角板画两条平行线a//b;
(2)一条截线c与这两条平行线相交;
(3)度量所形成的八个角
你测到的同位角相等吗? 2.动手操作,归纳性质 两条平行线被第三条直线截得的同位角会具有怎样的数量关系? 2.动手操作,归纳性质 如图,已知直线 a∥b ,c是截线. 两条平行线被第三条直线截得的同位角会具有怎样的数量关系? 2.动手操作,归纳性质性质1 两条平行线被第三条直线 所截,同位角相等. 2.动手操作,归纳性质性质1 两条平行线被第三条直线 所截,同位角相等. 两直线平行,同位角相等的应用 3.应用转化,推出性质 3.应用转化,推出性质性质2 两条平行线被第三条直线 所截,内错角相等.两条平行线被第三条直线截得的内错角会具有怎样的数量关系? 3.应用转化,推出性质性质2 两条平行线被第三条直线 所截,内错角相等. 3.应用转化,推出性质 3.应用转化,推出性质性质3 两条平行线被第三条直线 所截,同旁内角互补.两条平行线被第三条直线截得的同旁内角会具有怎样的数量关系? 3.应用转化,推出性质性质3 两条平行线被第三条直线 所截,同旁内角互补.(1)从∠1=110o.可以知道∠2是多少度吗?为什么?4.巩固新知,深化理解答:∠2 =110o.因为AB∥CD,∠1和∠2是内错角,根据两直线平行,内错角相等,得到∠1=∠2.因为∠1=110o,所以∠2 =110o.例1 如图,平行线AB,CD被直线AE所截.(2)从∠1=110o可以知道∠3是多少度吗?为什么?4.巩固新知,深化理解例1 如图,平行线AB,CD被直线AE所截.答:∠3 =110o.因为AB∥CD ,∠1和∠3是同位角,根据两直线平行,同位角相等,得到∠1=∠3.因为∠1=110o,所以∠3 =110o.(3)从∠1=110o可以知道∠4是多少度吗?为什么?4.巩固新知,深化理解例1 如图,平行线AB,CD被直线AE所截.答:∠4=70o.因为AB∥CD , ∠1和∠4是同旁内角,根据两直线平行,同旁内角互补,得到∠1+∠4=180o.因为∠1=110o,所以∠4=70o.例2 如图,已知AB∥CD,AE∥CF,∠A= 39°,
∠C是多少度?为什么? 4.巩固新知,深化理解方法一
解:∵AB∥CD,
∴ ∠C=∠1.
∵ AE∥CF,
∴ ∠A=∠1.
∴ ∠C=∠A.
∵∠A= 39o,
∴∠C= 39o.4.巩固新知,深化理解1方法二
解:∵AB∥CD,
∴ ∠C=∠2.
∵ AE∥CF,
∴ ∠A=∠2.
∴ ∠C=∠A.
∵∠A= 39o,
∴∠C= 39o.4.巩固新知,深化理解2(1)平行线的性质是什么?5.归纳小结(2)你能用自己的语言叙述研究平行线性质的过程吗? (3)性质2和性质3是通过简单推理得到的,在推理论证中需要注意哪些问题?教科书 习题5.3 第2、4、6题6.布置作业
