人教版七年级数学下册 5.2.2 平行线的判定课件(共21张PPT)
文档属性
| 名称 | 人教版七年级数学下册 5.2.2 平行线的判定课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 345.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-18 08:03:16 | ||
图片预览




文档简介
课件21张PPT。5.2.2平行线的判定1.下面说法中正确的是 ( ).
(1) 在同一平面内,两条直线的位置关系有相交、平行、垂直三种
(2) 在同一平面内, 不垂直的两条直线必平行
(3) 在同一平面内, 不平行的两条直线必垂直
(4) 在同一平面内,不相交的两条直线一定不垂直小测D1.下面说法中正确的是 ( ).
(1) 在同一平面内,两条直线的位置关系有相交、平行、垂直三种
(2) 在同一平面内, 不垂直的两条直线必平行
(3) 在同一平面内, 不平行的两条直线必垂直
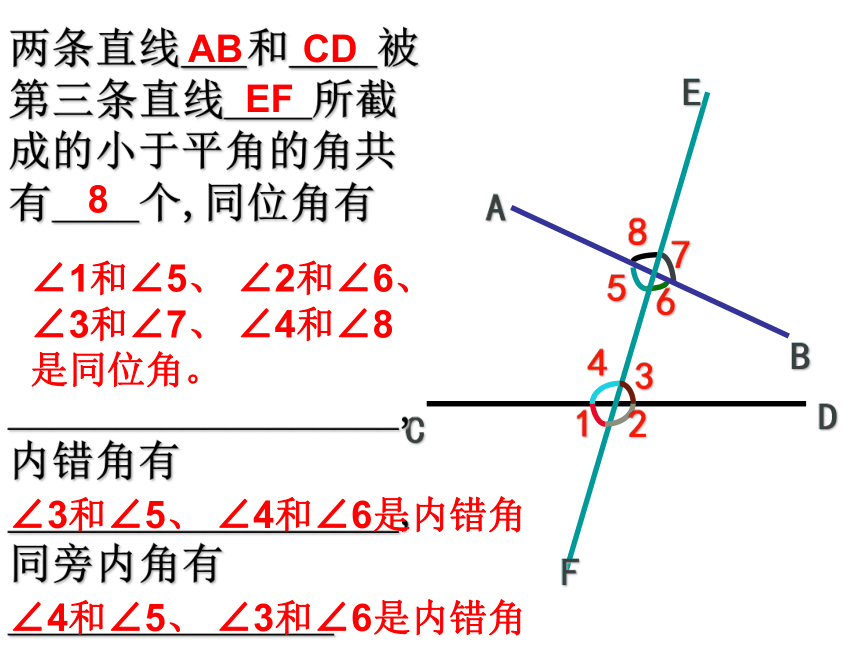
(4) 在同一平面内,不相交的两条直线一定不垂直小测D两条直线___和____被第三条直线____所截成的小于平角的角共有____个,同位角有
__________________,
内错角有__________________,
同旁内角有_______________ABEFCD8∠1和∠5、 ∠2和∠6、 ∠3和∠7、 ∠4和∠8
是同位角。∠3和∠5、 ∠4和∠6是内错角∠4和∠5、 ∠3和∠6是内错角学习目标:1、通过画平行线理解并记住平行线判定方法1;2、利用判定方法1推理说明判定方法2、3;
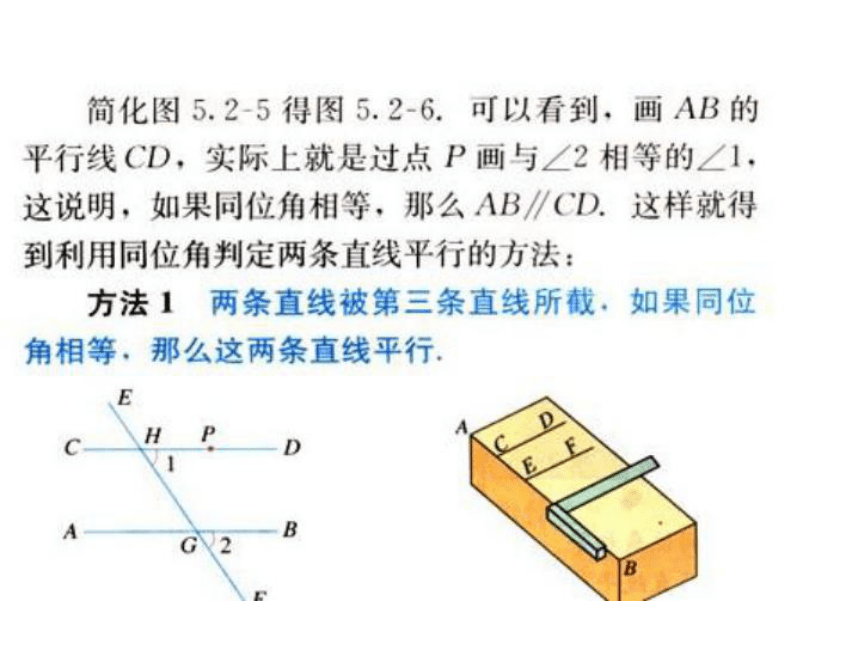
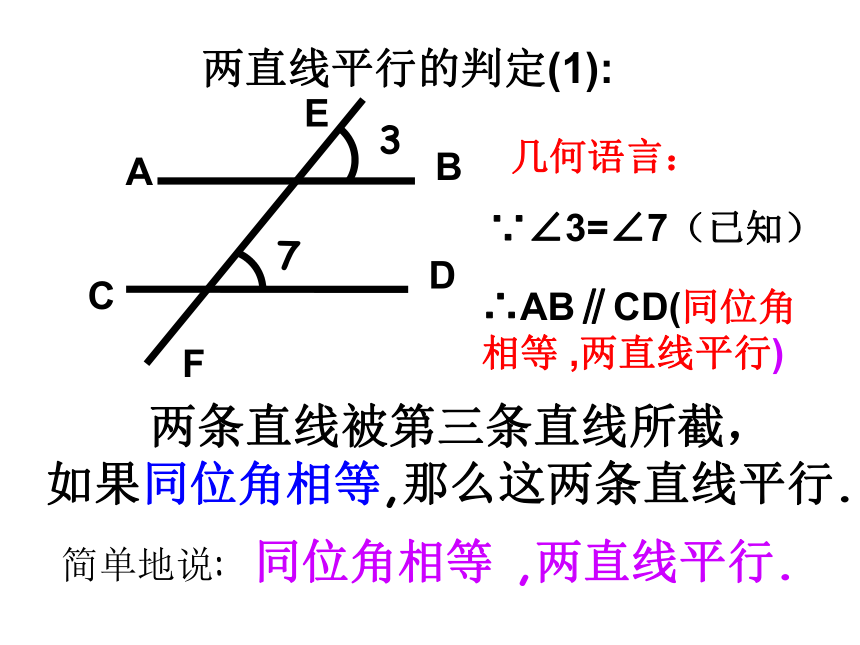
并记住判定方法2、3;3、综合运用判定方法1、2、3进行判断和说明。两直线平行的判定(1): 两条直线被第三条直线所截,
如果同位角相等,那么这两条直线平行.
简单地说: 同位角相等 ,两直线平行.
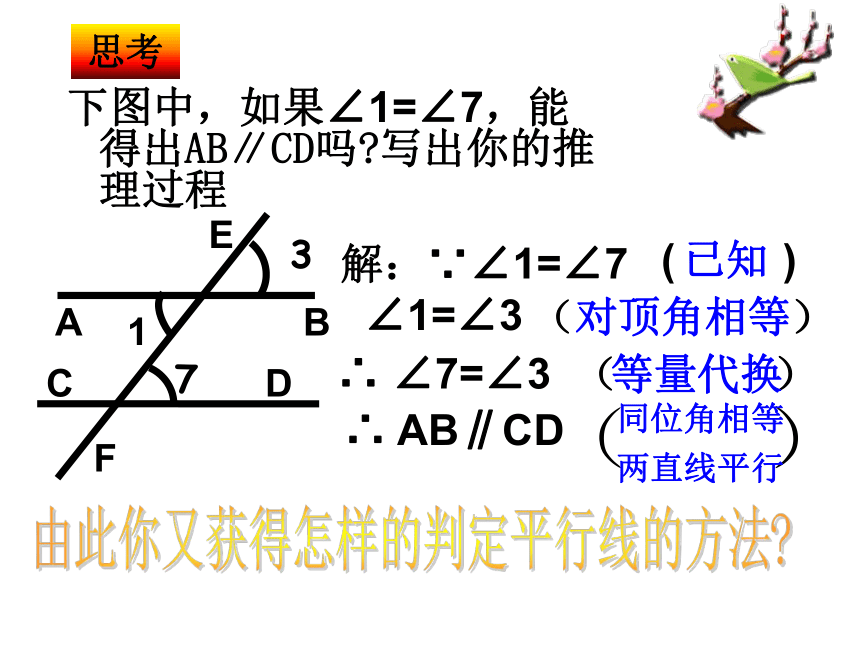
几何语言:∵∠3=∠7(已知)∴AB∥CD(同位角相等 ,两直线平行)下图中,如果∠1=∠7,能得出AB∥CD吗?写出你的推理过程思考解:∵∠1=∠7
∠1=∠3
∴ ∠7=∠3∴ AB∥CDB1ACDF37E由此你又获得怎样的判定平行线的方法?
( ) 已知 ( ) 对顶角相等( ) 等量代换 ( )
同位角相等
两直线平行 两直线平行的判定方法(2): 两条直线被第三条直线所截,
如果内错角相等,那么这两条直线平行.C简单地说: 内错角相等 ,两直线平行.几何语言:∵∠1=∠7(已知)∴AB∥CD(内错角相等 ,两直线平行)下图中,如果∠4+∠7=180°,
能得出AB∥CD?思考解:∵ ∠4+∠7=180 °(已知)
∠4+∠3=180°(邻补角的定义)
∴ ∠7=∠3(同角的补角相等)∴ AB∥CD(同位角相等, 两直线平行)1AC3478DBEF你还有其它的说理方法吗?下图中,如果∠4+∠7=180°,
能得出AB∥CD?思考1AC3478DBEF方法2解∵ ∠4+∠7=180 °(已知)
∠4+∠1=180°(邻补角的定义)∴ ∠7=∠1(同角的补角相等)∴ AB∥CD(内错角相等, 两直线平行)把你所悟到的证明一个真命题的方法,步骤,书写格式以及注意事项内化为一种方法.两直线平行的判定(3): 两条直线被第三条直线所截,
如果同旁内角互补,那么这两条直线平行.简单地说:同旁内角互补,两直线平行.几何语言:∵ ∠4+∠7=180 °(已知) ∴ AB∥CD
(同旁内角互补, 两直线平行) 1.如图,
(1)从∠1=∠2,可以推出 ∥
理由是
(2)从∠2=∠ ,可以推出c∥d ,
理由是
(3)如果∠4=75°,∠3=75 °,
可以推出 ∥
(4) 从∠4=75°,∠5= °,
可以推出a∥b.
考考你dba内错角相等,两直线平行同位角相等,两直线平行.3 cdc1052.如图,你可以添加哪些条件使得
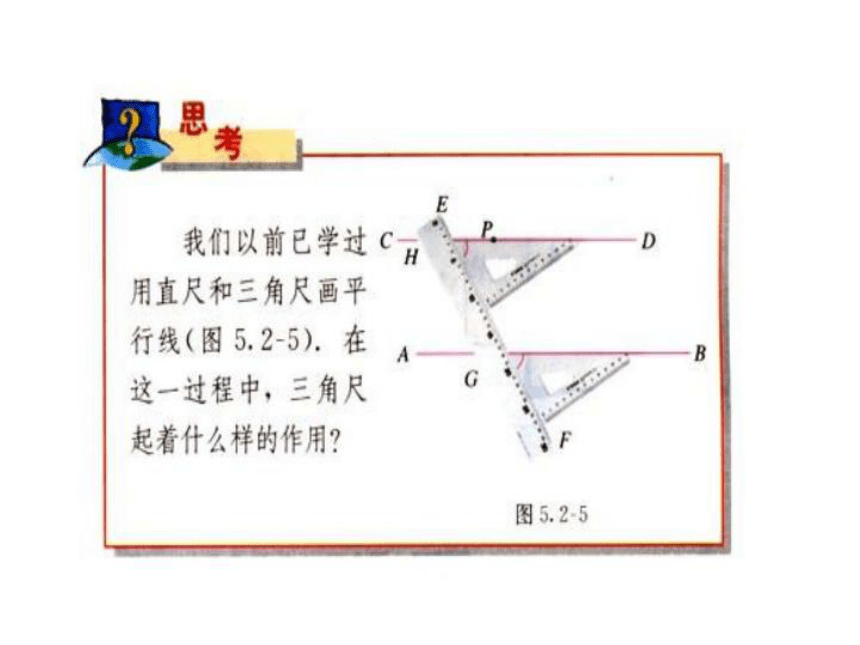
AB∥CD?考考你 小明用如图所示的方法作出了平行线,你认为他的作法对吗?为什么?平行线的判定?公理:
同位角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.判定定理1:
内错角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.判定定理2:
同旁内角互补,两直线平行.
∵∠1+∠2=1800 , ∴ a∥b. 这里的结论,以后可以直接运用. 如图:直线AB、CD都和AE相交,
且∠1+∠A=180o .
求证:AB//CDCBAD21E 证明:∵∠1+∠A=180o3测试:∴∠2+∠A=180o∴( )( )( )( )已知对顶角相等等量代换同旁内角互补,
两直线平行∠1=∠2AB∥CD探究:在同一平面内,如果两条直线垂直于同一条直线,那么这两条直线平行吗?为什么?已知:如图,直线AB⊥EF、CD⊥EF问:AB∥CD成立吗?为什么?小结通过这节课的学习,
你有哪些收获?议一议
(1) 在同一平面内,两条直线的位置关系有相交、平行、垂直三种
(2) 在同一平面内, 不垂直的两条直线必平行
(3) 在同一平面内, 不平行的两条直线必垂直
(4) 在同一平面内,不相交的两条直线一定不垂直小测D1.下面说法中正确的是 ( ).
(1) 在同一平面内,两条直线的位置关系有相交、平行、垂直三种
(2) 在同一平面内, 不垂直的两条直线必平行
(3) 在同一平面内, 不平行的两条直线必垂直
(4) 在同一平面内,不相交的两条直线一定不垂直小测D两条直线___和____被第三条直线____所截成的小于平角的角共有____个,同位角有
__________________,
内错角有__________________,
同旁内角有_______________ABEFCD8∠1和∠5、 ∠2和∠6、 ∠3和∠7、 ∠4和∠8
是同位角。∠3和∠5、 ∠4和∠6是内错角∠4和∠5、 ∠3和∠6是内错角学习目标:1、通过画平行线理解并记住平行线判定方法1;2、利用判定方法1推理说明判定方法2、3;
并记住判定方法2、3;3、综合运用判定方法1、2、3进行判断和说明。两直线平行的判定(1): 两条直线被第三条直线所截,
如果同位角相等,那么这两条直线平行.
简单地说: 同位角相等 ,两直线平行.
几何语言:∵∠3=∠7(已知)∴AB∥CD(同位角相等 ,两直线平行)下图中,如果∠1=∠7,能得出AB∥CD吗?写出你的推理过程思考解:∵∠1=∠7
∠1=∠3
∴ ∠7=∠3∴ AB∥CDB1ACDF37E由此你又获得怎样的判定平行线的方法?
( ) 已知 ( ) 对顶角相等( ) 等量代换 ( )
同位角相等
两直线平行 两直线平行的判定方法(2): 两条直线被第三条直线所截,
如果内错角相等,那么这两条直线平行.C简单地说: 内错角相等 ,两直线平行.几何语言:∵∠1=∠7(已知)∴AB∥CD(内错角相等 ,两直线平行)下图中,如果∠4+∠7=180°,
能得出AB∥CD?思考解:∵ ∠4+∠7=180 °(已知)
∠4+∠3=180°(邻补角的定义)
∴ ∠7=∠3(同角的补角相等)∴ AB∥CD(同位角相等, 两直线平行)1AC3478DBEF你还有其它的说理方法吗?下图中,如果∠4+∠7=180°,
能得出AB∥CD?思考1AC3478DBEF方法2解∵ ∠4+∠7=180 °(已知)
∠4+∠1=180°(邻补角的定义)∴ ∠7=∠1(同角的补角相等)∴ AB∥CD(内错角相等, 两直线平行)把你所悟到的证明一个真命题的方法,步骤,书写格式以及注意事项内化为一种方法.两直线平行的判定(3): 两条直线被第三条直线所截,
如果同旁内角互补,那么这两条直线平行.简单地说:同旁内角互补,两直线平行.几何语言:∵ ∠4+∠7=180 °(已知) ∴ AB∥CD
(同旁内角互补, 两直线平行) 1.如图,
(1)从∠1=∠2,可以推出 ∥
理由是
(2)从∠2=∠ ,可以推出c∥d ,
理由是
(3)如果∠4=75°,∠3=75 °,
可以推出 ∥
(4) 从∠4=75°,∠5= °,
可以推出a∥b.
考考你dba内错角相等,两直线平行同位角相等,两直线平行.3 cdc1052.如图,你可以添加哪些条件使得
AB∥CD?考考你 小明用如图所示的方法作出了平行线,你认为他的作法对吗?为什么?平行线的判定?公理:
同位角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.判定定理1:
内错角相等,两直线平行.
∵ ∠1=∠2, ∴ a∥b.判定定理2:
同旁内角互补,两直线平行.
∵∠1+∠2=1800 , ∴ a∥b. 这里的结论,以后可以直接运用. 如图:直线AB、CD都和AE相交,
且∠1+∠A=180o .
求证:AB//CDCBAD21E 证明:∵∠1+∠A=180o3测试:∴∠2+∠A=180o∴( )( )( )( )已知对顶角相等等量代换同旁内角互补,
两直线平行∠1=∠2AB∥CD探究:在同一平面内,如果两条直线垂直于同一条直线,那么这两条直线平行吗?为什么?已知:如图,直线AB⊥EF、CD⊥EF问:AB∥CD成立吗?为什么?小结通过这节课的学习,
你有哪些收获?议一议
