人教版七年级数学下册课件:5.1.2 垂线(共21张PPT)
文档属性
| 名称 | 人教版七年级数学下册课件:5.1.2 垂线(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 757.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-17 00:00:00 | ||
图片预览



文档简介
课件21张PPT。5.1 相交线(5.1.2 垂线)人教版七年级下册(一)创设情境、导入新课、
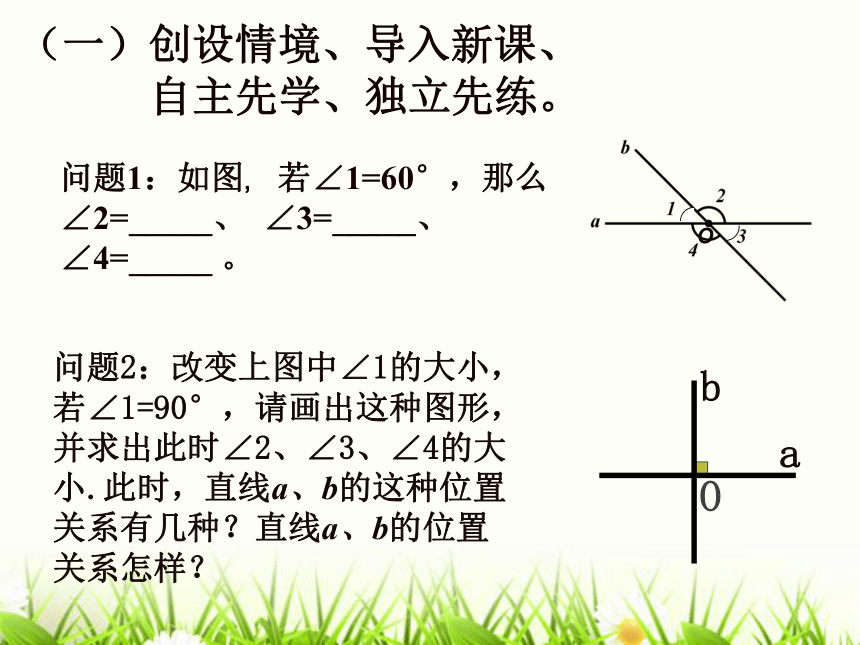
自主先学、独立先练。问题1:如图,若∠1=60°,那么
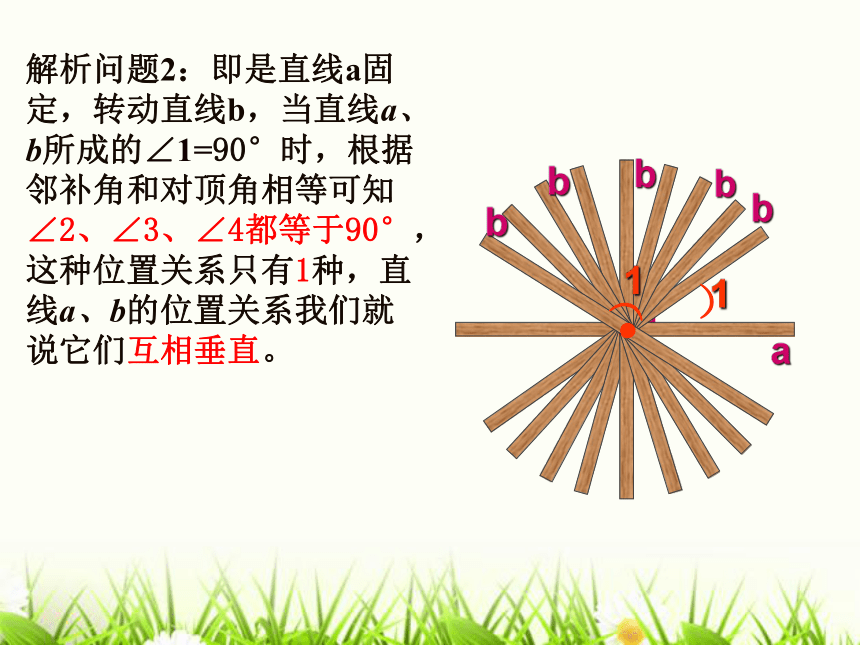
∠2=_____、 ∠3=_____、∠4=_____ 。问题2:改变上图中∠1的大小,若∠1=90°,请画出这种图形,并求出此时∠2、∠3、∠4的大小.此时,直线a、b的这种位置关系有几种?直线a、b的位置关系怎样?O)1 abbbbb)1 解析问题2:即是直线a固定,转动直线b,当直线a、b所成的∠1=90°时,根据邻补角和对顶角相等可知∠2、∠3、∠4都等于90°,这种位置关系只有1种,直线a、b的位置关系我们就说它们互相垂直。
1、垂直的概念(二)小组合作、共同探究、
归纳新知,达标测评。(1) 小组合作、共同探究:探讨问题2,垂直是相交的一种特殊情形,请用文字叙述垂直、垂线的定义,并用几何语言表示。①.垂直定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。例如、问题2,a、b互相垂直,O叫垂足.a叫b的垂线,b也叫a的垂线。从垂直的定义可知,
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个交角中一个角是直角。(2)归纳新知:②.垂直的表示方法:
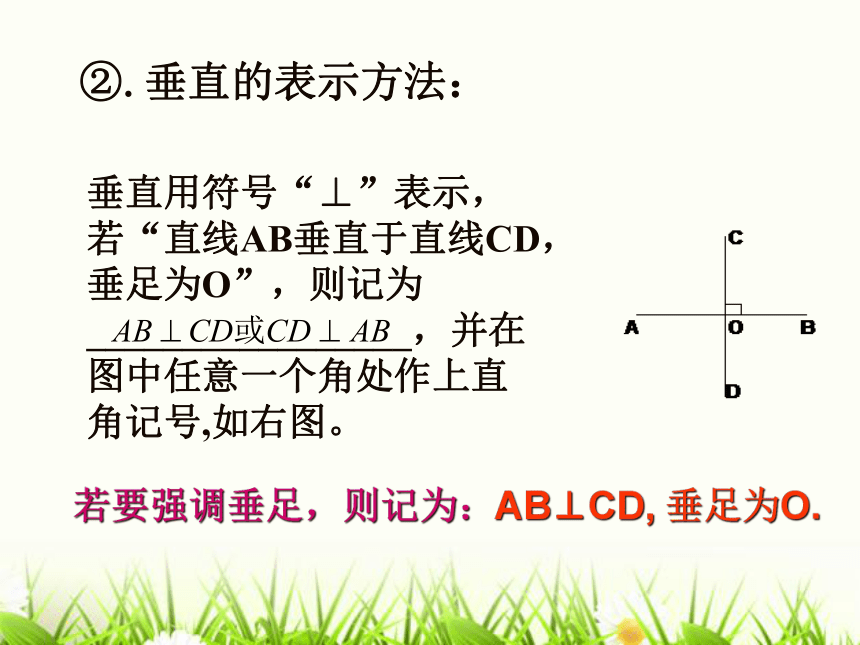
垂直用符号“⊥”表示,若“直线AB垂直于直线CD, 垂足为O”,则记为_________________,并在图中任意一个角处作上直角记号,如右图。若要强调垂足,则记为:AB⊥CD, 垂足为O.ABCDO几何语言: 如图,当直线AB与CD相交于O点,∠AOD=90°时,那么AB⊥CD,垂足为O。∵∠AOD=90°(已知)
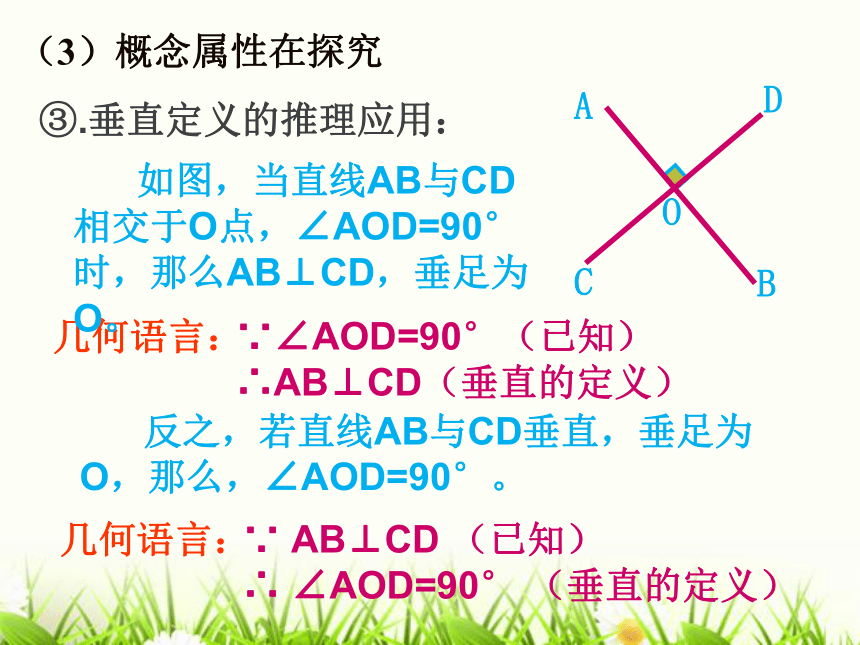
∴AB⊥CD(垂直的定义)几何语言: 反之,若直线AB与CD垂直,垂足为O,那么,∠AOD=90°。③.垂直定义的推理应用:∵ AB⊥CD (已知)
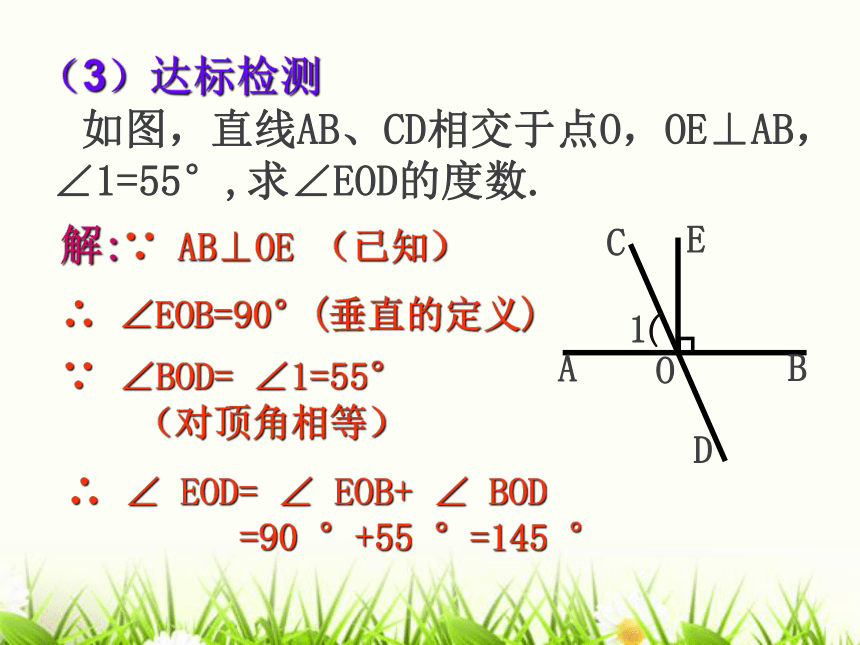
∴ ∠AOD=90° (垂直的定义)(3)概念属性在探究 如图,直线AB、CD相交于点O,OE⊥AB,∠1=55°,求∠EOD的度数.ACEBDO1∴ ∠EOB=90°(垂直的定义) ∴ ∠ EOD= ∠ EOB+ ∠ BOD
=90 °+55 °=145 °(解:∵ AB⊥OE (已知)∵ ∠BOD= ∠1=55°
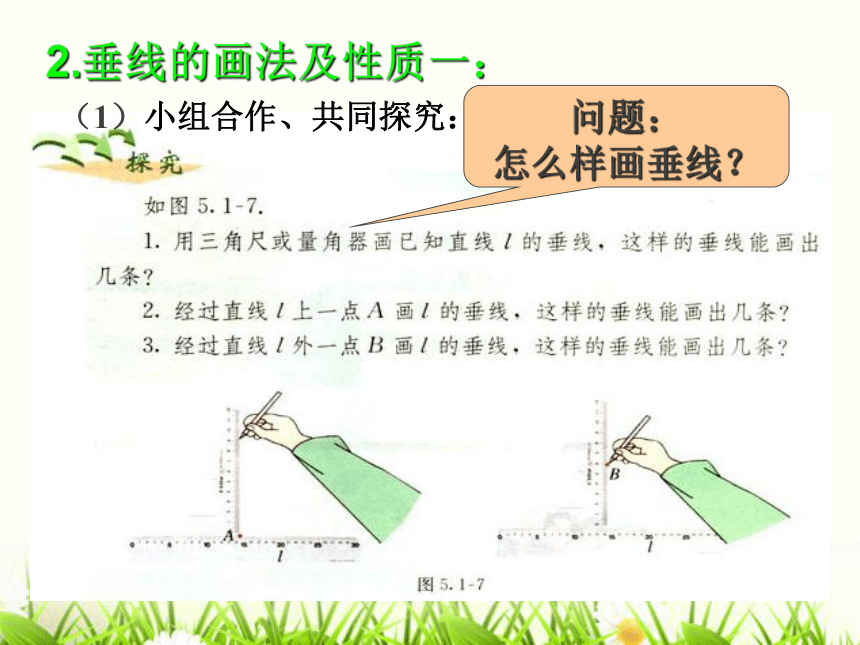
(对顶角相等)(3)达标检测问题:
怎么样画垂线?2.垂线的画法及性质一:(1)小组合作、共同探究:问题1:画已知直线l的垂线,这样的垂线能画出几条?1放、
2靠、
3画线、lO如图,已知直线 l,作l的垂线。工具:直尺、三角板或量角器无数条lA问题2:已知直线 l 和l上的一点A ,过点A作l的垂线.C4画线:沿着三角板的另一直角边画出垂线.1放:放直尺,直尺的一边要与已知直线重合;3移:移动三角板到已知点;2靠:靠三角板,把三角板的一直角边靠在直尺上; 则所画直线AC是过点A的直线l的垂线.lB问题3:已知直线 l 和l外的一点B ,过点B作l的垂线.D4画线:沿着三角板的另一直角边画出垂线.1放:放直尺,直尺的一边要与已知直线重合;3移:移动三角板到已知点;2靠:靠三角板,把三角板的一直角边靠在直尺上; 则所画直线BD是过点B的直线l的垂线.请同学们画一下 结论:
过一点有且只有一条直线与已知直线垂直.能作一条,而且只能作一条.问题4:过已知直线 l 和l上(或外)的一点A ,作l的垂线,可以作几条? 注意:
过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.(2)归纳新知:(3)达标检测①请你过点P画出线段AB和射线OA的垂线注意:画线段(或射线)的垂线时,有时要将线段延长(或将射线反向延长)后再画垂线. 此问题就是“直线外一点与已知直线上各点所连的线段中,有没有最短的线段?”P3、垂线的性质二及点到直线的距离问题1:(1)小组合作、共同探究:两点之间,线段最短问题2:上学期我们曾经学过什么最短的知识,还记得吗?P问题3:上面问题1可以转化为数学问题:“已知直线l和直线外一点P,连接点P到直线l上各点O,A1,A2,A3…,其中 PO⊥l(我们称PO为点P到直线l的垂线段)。 请你画图,并用
尺量一下,看看哪
一条线段最短?
连接直线外一点与直线上各点的所有线段中,垂线段最短。垂线段最短直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。PClD垂线段的长度简单说成:垂线段最短.A2A3A4A1O(2)归纳新知: ①如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?请画出图来,并说明理由。C∟垂线段最短(3)达标检测②.如图, AC⊥BC, ∠C=900 ,线段AC、BC、CD中最短的是( )
(A) AC (B) BC (C) CD (D) 不能确定DABCC回忆两条直线相交这部分知识,并问:你们能够把它们画成一个知识结构图吗? 小结
自主先学、独立先练。问题1:如图,若∠1=60°,那么
∠2=_____、 ∠3=_____、∠4=_____ 。问题2:改变上图中∠1的大小,若∠1=90°,请画出这种图形,并求出此时∠2、∠3、∠4的大小.此时,直线a、b的这种位置关系有几种?直线a、b的位置关系怎样?O)1 abbbbb)1 解析问题2:即是直线a固定,转动直线b,当直线a、b所成的∠1=90°时,根据邻补角和对顶角相等可知∠2、∠3、∠4都等于90°,这种位置关系只有1种,直线a、b的位置关系我们就说它们互相垂直。
1、垂直的概念(二)小组合作、共同探究、
归纳新知,达标测评。(1) 小组合作、共同探究:探讨问题2,垂直是相交的一种特殊情形,请用文字叙述垂直、垂线的定义,并用几何语言表示。①.垂直定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。例如、问题2,a、b互相垂直,O叫垂足.a叫b的垂线,b也叫a的垂线。从垂直的定义可知,
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个交角中一个角是直角。(2)归纳新知:②.垂直的表示方法:
垂直用符号“⊥”表示,若“直线AB垂直于直线CD, 垂足为O”,则记为_________________,并在图中任意一个角处作上直角记号,如右图。若要强调垂足,则记为:AB⊥CD, 垂足为O.ABCDO几何语言: 如图,当直线AB与CD相交于O点,∠AOD=90°时,那么AB⊥CD,垂足为O。∵∠AOD=90°(已知)
∴AB⊥CD(垂直的定义)几何语言: 反之,若直线AB与CD垂直,垂足为O,那么,∠AOD=90°。③.垂直定义的推理应用:∵ AB⊥CD (已知)
∴ ∠AOD=90° (垂直的定义)(3)概念属性在探究 如图,直线AB、CD相交于点O,OE⊥AB,∠1=55°,求∠EOD的度数.ACEBDO1∴ ∠EOB=90°(垂直的定义) ∴ ∠ EOD= ∠ EOB+ ∠ BOD
=90 °+55 °=145 °(解:∵ AB⊥OE (已知)∵ ∠BOD= ∠1=55°
(对顶角相等)(3)达标检测问题:
怎么样画垂线?2.垂线的画法及性质一:(1)小组合作、共同探究:问题1:画已知直线l的垂线,这样的垂线能画出几条?1放、
2靠、
3画线、lO如图,已知直线 l,作l的垂线。工具:直尺、三角板或量角器无数条lA问题2:已知直线 l 和l上的一点A ,过点A作l的垂线.C4画线:沿着三角板的另一直角边画出垂线.1放:放直尺,直尺的一边要与已知直线重合;3移:移动三角板到已知点;2靠:靠三角板,把三角板的一直角边靠在直尺上; 则所画直线AC是过点A的直线l的垂线.lB问题3:已知直线 l 和l外的一点B ,过点B作l的垂线.D4画线:沿着三角板的另一直角边画出垂线.1放:放直尺,直尺的一边要与已知直线重合;3移:移动三角板到已知点;2靠:靠三角板,把三角板的一直角边靠在直尺上; 则所画直线BD是过点B的直线l的垂线.请同学们画一下 结论:
过一点有且只有一条直线与已知直线垂直.能作一条,而且只能作一条.问题4:过已知直线 l 和l上(或外)的一点A ,作l的垂线,可以作几条? 注意:
过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.(2)归纳新知:(3)达标检测①请你过点P画出线段AB和射线OA的垂线注意:画线段(或射线)的垂线时,有时要将线段延长(或将射线反向延长)后再画垂线. 此问题就是“直线外一点与已知直线上各点所连的线段中,有没有最短的线段?”P3、垂线的性质二及点到直线的距离问题1:(1)小组合作、共同探究:两点之间,线段最短问题2:上学期我们曾经学过什么最短的知识,还记得吗?P问题3:上面问题1可以转化为数学问题:“已知直线l和直线外一点P,连接点P到直线l上各点O,A1,A2,A3…,其中 PO⊥l(我们称PO为点P到直线l的垂线段)。 请你画图,并用
尺量一下,看看哪
一条线段最短?
连接直线外一点与直线上各点的所有线段中,垂线段最短。垂线段最短直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。PClD垂线段的长度简单说成:垂线段最短.A2A3A4A1O(2)归纳新知: ①如图:要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?请画出图来,并说明理由。C∟垂线段最短(3)达标检测②.如图, AC⊥BC, ∠C=900 ,线段AC、BC、CD中最短的是( )
(A) AC (B) BC (C) CD (D) 不能确定DABCC回忆两条直线相交这部分知识,并问:你们能够把它们画成一个知识结构图吗? 小结
