17.1 勾股定理同步测试题（含解析）

中小学教育资源及组卷应用平台


人教版2019-2020学年八年级下学期
17.1勾股定理
（时间60分钟 总分100分）
一、选择题（每小题5分，共30分）
1.高为3，底边长为8的等腰三角形腰长为（ ）
A.3 B.4 C.5 D.6
2.直角三角形两直角边分别为5、12，则这个直角三角形斜边上的高为（ ）
A.6 B.8.5 C. D.
3.若三角形三边长为a、b、c，且满足等式，则此三角形是（ ）
A.锐角三角形 B.钝角三角形 C.等腰直角三角形 D.直角三角形
4.如图，直角三角形ABC的周长为24，且AB:BC=5：3，则AC=（ ）

A.6 B.8 C.10 D.12
5.已知，如图，四边形ABCD中，AB=3cm，AD=4cm，BC=13cm，CD=12cm，且∠A=90°，则四边形ABCD的面积为（ ）

A.36 B.22 C.18 D.12
6.已知，如图长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则ABE的面积为（ ）

A.6cm B.8cm C.10cm D.12cm
二、填空题（每小题5分，共20分）
7.在RtABC中，AC=5，BC=12，则AB边的长是_________
8.如图（1）、（2）中，（1）正方形A的面积为_______.（2）斜边x=_______

9.如图，在一个高为3米，长为5米的楼梯表面铺地毯，则地毯长度为_____米

10.等腰ABC的面积为12cm，底上的高AD=3cm，则它的周长为______cm.
三、解答题（共5题，共50分）
11.已知：如图，AD=4，CD=3，∠ADC=90°，AB=13，∠ACB=90°，求图形中阴影部分的面积.




12.如图，在ABC中，∠ACB=90°，CDAB于点D，AC=12cm，BC=16cm，求AD、CD的长.









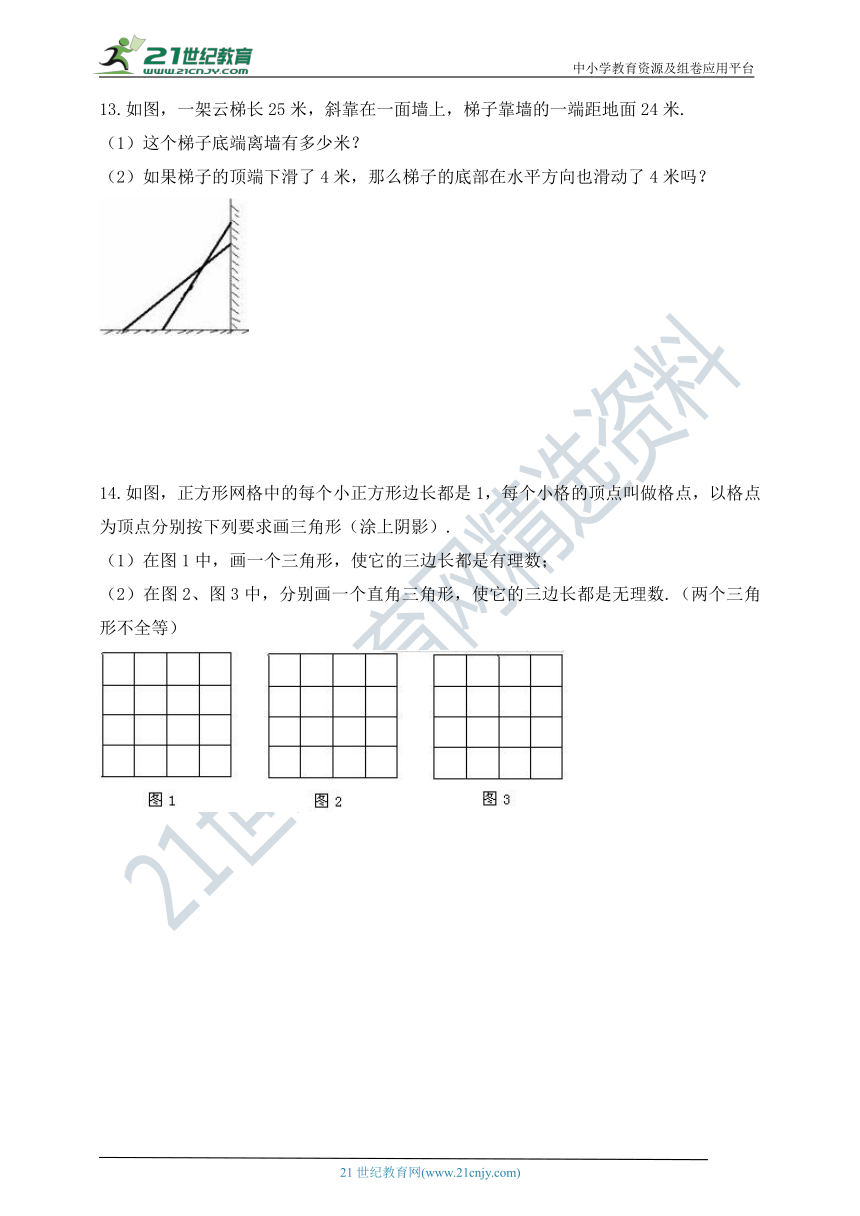
13.如图，一架云梯长25米，斜靠在一面墙上，梯子靠墙的一端距地面24米.
（1）这个梯子底端离墙有多少米？
（2）如果梯子的顶端下滑了4米，那么梯子的底部在水平方向也滑动了4米吗？





14.如图，正方形网格中的每个小正方形边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形（涂上阴影）.
（1）在图1中，画一个三角形，使它的三边长都是有理数；
（2）在图2、图3中，分别画一个直角三角形，使它的三边长都是无理数.（两个三角形不全等）










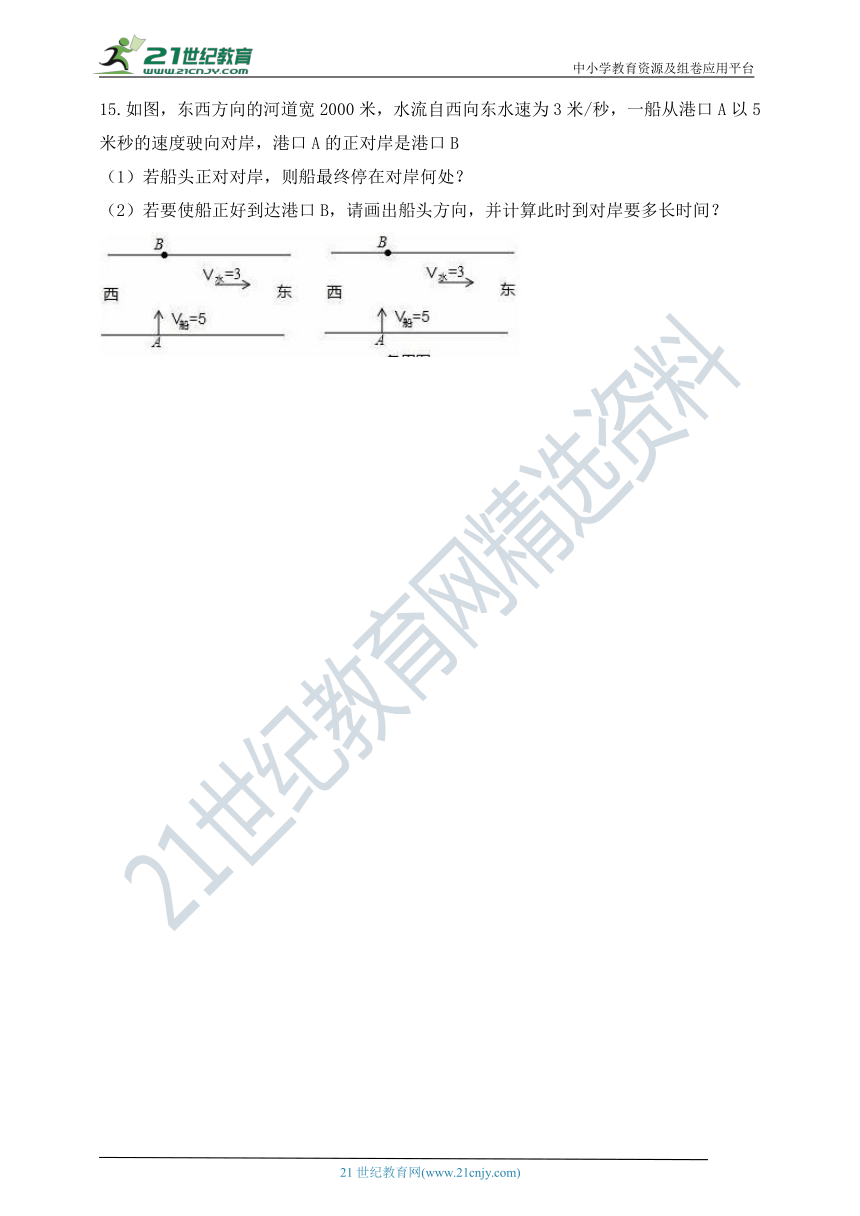
15.如图，东西方向的河道宽2000米，水流自西向东水速为3米/秒，一船从港口A以5米秒的速度驶向对岸，港口A的正对岸是港口B
（1）若船头正对对岸，则船最终停在对岸何处？
（2）若要使船正好到达港口B，请画出船头方向，并计算此时到对岸要多长时间？





















答案
1.【解析】，，，，又AD=3，在RtABD中，AB===5，故选C。

2.【解析】由勾股定理可得：斜边长,则斜边长=13，直角三角形面积
斜边的高，可得：斜边的高,故选D.
3.【解析】,,所以为直角三角形,故选D.
4.【解析】设AB=5x，BC=3x，在RtACB中，由勾股定理得：
,直角三角形ABC的周长为：5x+4x+3x=24，x=2，所以，AC=2×4=8，故选B.
5.【解析】连接BD，,=5cm，
，，，
，.四边形ABCD的面积为30+6=36（cm）,故选A。
6.【解析】由于长方形折叠，使点B与点D重合，所以ED=BE，设AE=xcm，则ED=BE=（9-x）cm，在RtABE中，，，解得：x=4，所以△ABE的面积为，故选A
7.【解析】（1）当AC、BC为直角边时，根据勾股定理得：

（2）当BC为斜边，AC为直角边时，根据勾股定理得：
8.【解析】（1）设A的边长为a，如图（1）所示：在该直角三角形中，由勾股定理可得：，所以正方形A的面积为a=36.
（2）如图（2）所示：在该直角三角形中，由勾股定理可得：，所以，斜边x=13.
9.【解析】由勾股定理得：，所以地毯的长度为4+3=7米。故答案为：7.
10.【解析】设底为a，则,，根据勾股定理得，
,所以腰为5，因此周长为5+5+8=18cm.

11.【解析】在RtACD中，
在RtACB中，
，，所以阴影部分面积为30-6=24
12.【解析】因为∠ACB=90°，AC=12cm,BC=16cm,AB=20cm.根据直角三角形的面积公式，得，在RtACD中
13.【解析】（1）7米；（2）不是设滑动后梯子的底端到墙的距离为x米，得方程，
，解得x=15，所以梯子向后滑动了8米。
14.【解析】

15.【解析】解：（1）2000-5=400（秒），
3×400=1200（米）.
答：船最终停在港口B东边的1200米处.
（2）在RtACD中，AC=5米/秒，CD=3米秒，
20004=500（秒）.答：此时到对岸要500秒钟.








21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）



HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)