人教版高中物理必修二第五章第二节 运动的合成与分解 (共44页).pptx
文档属性
| 名称 | 人教版高中物理必修二第五章第二节 运动的合成与分解 (共44页).pptx |  | |
| 格式 | zip | ||
| 文件大小 | 860.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-03-17 22:36:17 | ||
图片预览








文档简介
(共44张PPT)
课前检测
什么是合力合分力?
力(矢量)的合成和分解遵循什么原则?
物体做直线运动的条件是什么?
课程标准:
会用运动合成与分解的方法分析抛体运动。
学习目标:
1、理解运动的独立性、合运动与分运动
2、掌握运动的合成与分解的方法-平行四边形定则
3、会用平行四边形定则分析速度、位移的合成与分解的问题
运动的合成与分解
提出问题
物体的运动轨迹不是直线
比如我们将网球以某个角度抛出,其运动的轨迹不是直线而是曲线。
网球运动的频闪照片
思考:曲线运动与直线运动除了运动轨迹不同,还有什么显著不同?
直线运动物体速度的方向
曲线运动物体速度的方向
时刻改变
不变
?
怎样确定曲线运动中任意时刻(或任意位置)的速度方向呢?
1、定义:运动轨迹是曲线的运动叫做曲线运动。
A
曲线运动
砂轮
2、曲线运动的速度方向:做曲线运动的质点在某一点(或某一时刻)的速度方向是在曲线的这一点的切线方向; zxxk
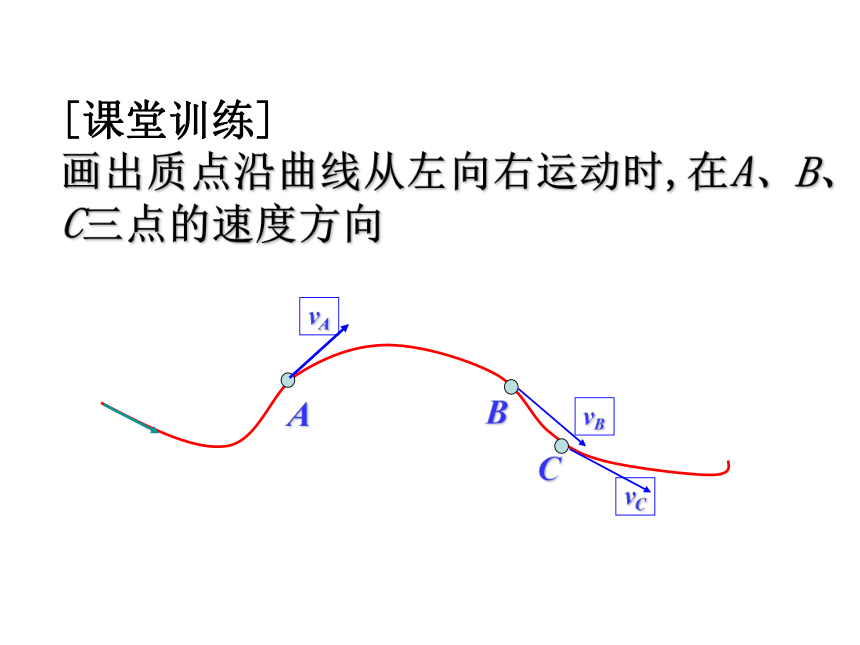
[课堂训练]
画出质点沿曲线从左向右运动时,在A、B、C三点的速度方向学科网
A
B
C
vA
vB
vC
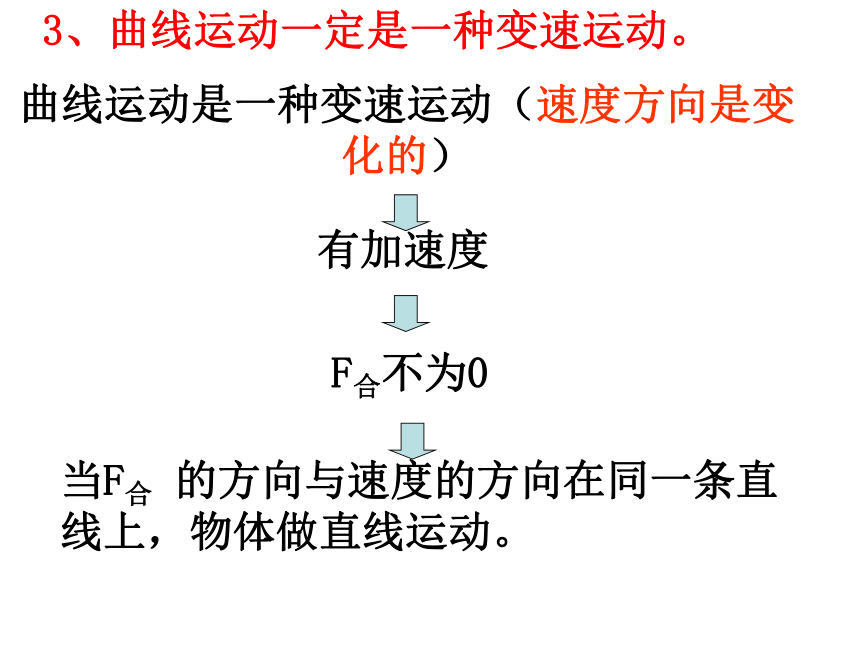
曲线运动是一种变速运动(速度方向是变化的)
有加速度
F合不为0
当F合 的方向与速度的方向在同一条直线上,物体做直线运动。
3、曲线运动一定是一种变速运动。
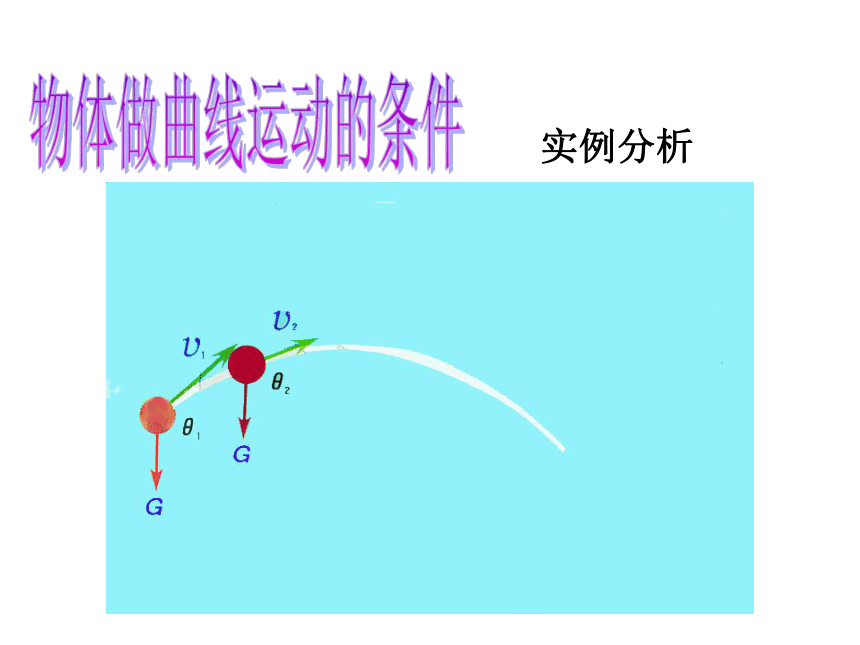
物体做曲线运动的条件
实例分析
物体什么时候做曲线运动呢?
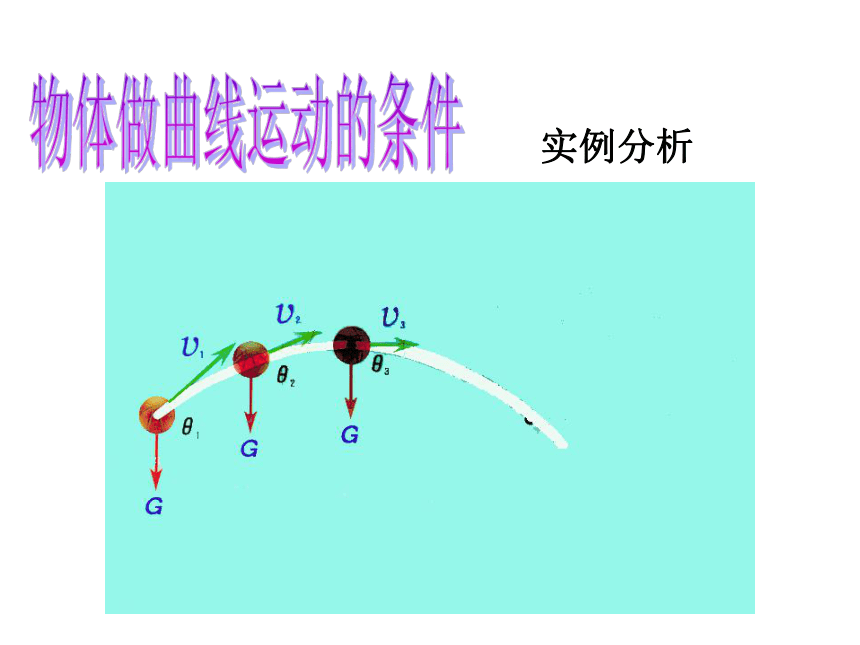
物体做曲线运动的条件
实例分析
物体做曲线运动的条件
实例分析
物体做曲线运动的条件
实例分析1
物体做曲线运动的条件
实例分析组.卷.网
物体所受合外力的方向跟它速度的方向不在同一条直线上;
加速度方向和速度方向不在一条直线上,物体做曲线运动
从运动学角度:
4、物体做曲线运动的条件:
F合或 a 跟 v 在同一直线上
直线运动
a 恒定→匀变速直线运动
a 变化→变加速直线运动
F合或 a 跟 v 不在同一直线上
曲线运动
a 恒定→匀变速曲线运动
a 变化→变加速曲线运动
说明:判断直线还是曲线运动关键看a 与v 是否同一直线;判断匀变速还是变加速关键看a 是否恒定
总结
做曲线运动的物体运动轨迹、速度方向与其所受合外力方向三者位置关系如何?
【思考】
5、做曲线运动的物体所受合外力必定指向运动轨迹的内侧(或轨迹弯曲的一侧)。
怎样研究、描述这样的曲线运动呢?
观察红蜡烛的运动情况
运动的合成和分解
2.运动的合成和分解的方法
速度、位移、加速度的合成和分解——遵循平行四边形定则
1)合运动:物体实际的运动
2)分运动:与合运动等效的其它方向的运动
3)运动的合成:已知分运动求合运动
4)运动的分解:已知合运动求分运动
1.几个基本概念
x1
x2
x
v1
v2
v
a1
a2
a
x1
x2
x
3.合运动与分运动的关系
1)等效性:合运动的效果与各分运动共同产生的效果相同。
2)等时性:合运动与分运动所用时间相同。
3)独立性:各分运动各自按自己的规律运动,互不干扰。
合运动与分运动的区分原则:物体实际进行的运动一定是合运动,对应于平行四边形的对角线.
1)是直线运动还是曲线运动?(判断轨迹)
2)是匀变速运动还是变加速运动?(判断运动性质)
思考:如何判断两个直线运动的合运动的运动轨迹和运动性质?
合力F合的方向或加速度a的方向与合速度v合的方向是否同一直线
合力或加速度是否恒定
判断:不在一直线上的两个匀速直线运动的合运动?一个匀速直线运动与一个匀加速直线运动的合运动?两个匀变速直线运动的合运动?
v2
v
v2
v1
a1
a2
a
v1
v
a1
a2
a
加速直线运动
加速曲线运动
画图分析两个加速运动的合成
1、两互成角度的匀速直线运动的合成
匀速直线运动
2、两互成角度的初速为零的匀加速直线运动的合成
匀加速直线运动
3、两互成角度的初速不为零的匀加速直线运动的合成
匀变速直线运动或匀变速曲线运动
4、一个匀速直线运动和一个匀加速直线运动的合成
匀变速直线运动或匀变速曲线运动
方法1.按运动的实际效果分解
方法2.正交分解
1)分解的原则
2)运动分解的典型问题
a.渡船问题的分解
b.拉绳问题的分解
4.运动的分解
合运动与分运动
【例1】关于互成角度的两个初速度不为0的匀变速直线运动的合运动,下述说法正确的是( )
A.一定是直线运动
B.一定是抛物线运动
C.可能是直线运动,也可能是抛物线运动
D.以上说法都不对
C
2.关于运动的合成,下列说法中正确的( )
A.合运动的速度一定比每一个分运动的速度大
B.两个分运动的时间一定与它们合运动的时间相等
C.只要两个分运动是直线运动,合运动一定是直线运动
D.两个匀变速直线运动的合运动一定是匀变速直线运动
B
例1:一艘小船在100m宽的河中横渡到对岸,已知水流速度是3m/s,小船在静水中的速度是4m/s,求:
欲使船渡河时间最短,船应该怎样渡河?最短时间是多少?船经过的位移多大?
运动的合成和分解的应用:小船渡河
分析1:时间最短
d
结论:欲使船渡河时间最短,船头的方向应该垂直于河岸。
解1:当船头垂直河岸时,所用时间最短
最短时间
此时合速度
此时航程
例2:一艘小船在100m宽的河中横渡到对岸,已知水流速度是3m/s,小船在静水中的速度是4m/s,求:
欲使航行距离最短,船应该怎样渡河?渡河时间多长?
分析2:航程最短
θ
d
设船头指向与上游河岸成θ:
结论:当v船>v水时,最短航程等于河宽d。
解:2、当船头指向斜上游,与岸夹角为?时,合运动垂直河岸,航程最短,数值等于河宽100米。
过河时间:
合速度:
则cos ? =
小船过河
假如船不动 水流动
V水
小船过河
假如水不流动 船动
V船
小船过河问题
V水
V船
小船过河问题
V水
V船
问题拓展
1、在船头始终垂直对岸的情况下,在行驶到河中间时,水流速度突然增大,过河时间如何变化?
2、为了垂直到达河对岸,在行驶到河中间时,水流速度突然增大,过河时间如何变化?
答案:变长
答案:不变
【例题】如图所示,纤绳以恒定速率v沿水平方向通过定滑轮牵引小船靠岸,当纤绳与水面夹角为θ时,船靠岸的速度是 ,若使船匀速靠岸,则纤绳的速度是 。(填:匀速、加速、减速)
减速
运动的合成和分解的应用:绳物模型
注:物体的实际运动为合运动
练习如图所示,汽车沿水平路面以恒定速度v前进,则当拉绳与水平方向成θ角时,被吊起的物体M的速度为vM= 。
【答案】
选做:若河宽仍为100m,已知水流速度是4m/s,小船在静水中的速度是3m/s,即船速(静水中)小于水速。
求:
(1)欲使船渡河时间最短,船应该怎样渡河?
(2)欲使航行距离最短,船应该怎样渡河?最短航线是河宽吗?
θ
θ
结论:当v船< v水时,最短航程不等于河宽d。
船头指向与上游河岸成θ:
小结
探究曲线运动的基本方法——运动的合成与分解.这种方法在应用过程中遵循平行四边形定则.在实际的解题过程中,通常选择实际看到的运动为合运动,其他的运动为分运动.运动的合成与分解包括以下几方面的内容:
(1)速度的合成与分解;
(2)位移的合成与分解;
(3)加速度的合成与分解.
合运动与分运动之间还存在如下的特点:
独立性;等效性;等时性
课前检测
什么是合力合分力?
力(矢量)的合成和分解遵循什么原则?
物体做直线运动的条件是什么?
课程标准:
会用运动合成与分解的方法分析抛体运动。
学习目标:
1、理解运动的独立性、合运动与分运动
2、掌握运动的合成与分解的方法-平行四边形定则
3、会用平行四边形定则分析速度、位移的合成与分解的问题
运动的合成与分解
提出问题
物体的运动轨迹不是直线
比如我们将网球以某个角度抛出,其运动的轨迹不是直线而是曲线。
网球运动的频闪照片
思考:曲线运动与直线运动除了运动轨迹不同,还有什么显著不同?
直线运动物体速度的方向
曲线运动物体速度的方向
时刻改变
不变
?
怎样确定曲线运动中任意时刻(或任意位置)的速度方向呢?
1、定义:运动轨迹是曲线的运动叫做曲线运动。
A
曲线运动
砂轮
2、曲线运动的速度方向:做曲线运动的质点在某一点(或某一时刻)的速度方向是在曲线的这一点的切线方向; zxxk
[课堂训练]
画出质点沿曲线从左向右运动时,在A、B、C三点的速度方向学科网
A
B
C
vA
vB
vC
曲线运动是一种变速运动(速度方向是变化的)
有加速度
F合不为0
当F合 的方向与速度的方向在同一条直线上,物体做直线运动。
3、曲线运动一定是一种变速运动。
物体做曲线运动的条件
实例分析
物体什么时候做曲线运动呢?
物体做曲线运动的条件
实例分析
物体做曲线运动的条件
实例分析
物体做曲线运动的条件
实例分析1
物体做曲线运动的条件
实例分析组.卷.网
物体所受合外力的方向跟它速度的方向不在同一条直线上;
加速度方向和速度方向不在一条直线上,物体做曲线运动
从运动学角度:
4、物体做曲线运动的条件:
F合或 a 跟 v 在同一直线上
直线运动
a 恒定→匀变速直线运动
a 变化→变加速直线运动
F合或 a 跟 v 不在同一直线上
曲线运动
a 恒定→匀变速曲线运动
a 变化→变加速曲线运动
说明:判断直线还是曲线运动关键看a 与v 是否同一直线;判断匀变速还是变加速关键看a 是否恒定
总结
做曲线运动的物体运动轨迹、速度方向与其所受合外力方向三者位置关系如何?
【思考】
5、做曲线运动的物体所受合外力必定指向运动轨迹的内侧(或轨迹弯曲的一侧)。
怎样研究、描述这样的曲线运动呢?
观察红蜡烛的运动情况
运动的合成和分解
2.运动的合成和分解的方法
速度、位移、加速度的合成和分解——遵循平行四边形定则
1)合运动:物体实际的运动
2)分运动:与合运动等效的其它方向的运动
3)运动的合成:已知分运动求合运动
4)运动的分解:已知合运动求分运动
1.几个基本概念
x1
x2
x
v1
v2
v
a1
a2
a
x1
x2
x
3.合运动与分运动的关系
1)等效性:合运动的效果与各分运动共同产生的效果相同。
2)等时性:合运动与分运动所用时间相同。
3)独立性:各分运动各自按自己的规律运动,互不干扰。
合运动与分运动的区分原则:物体实际进行的运动一定是合运动,对应于平行四边形的对角线.
1)是直线运动还是曲线运动?(判断轨迹)
2)是匀变速运动还是变加速运动?(判断运动性质)
思考:如何判断两个直线运动的合运动的运动轨迹和运动性质?
合力F合的方向或加速度a的方向与合速度v合的方向是否同一直线
合力或加速度是否恒定
判断:不在一直线上的两个匀速直线运动的合运动?一个匀速直线运动与一个匀加速直线运动的合运动?两个匀变速直线运动的合运动?
v2
v
v2
v1
a1
a2
a
v1
v
a1
a2
a
加速直线运动
加速曲线运动
画图分析两个加速运动的合成
1、两互成角度的匀速直线运动的合成
匀速直线运动
2、两互成角度的初速为零的匀加速直线运动的合成
匀加速直线运动
3、两互成角度的初速不为零的匀加速直线运动的合成
匀变速直线运动或匀变速曲线运动
4、一个匀速直线运动和一个匀加速直线运动的合成
匀变速直线运动或匀变速曲线运动
方法1.按运动的实际效果分解
方法2.正交分解
1)分解的原则
2)运动分解的典型问题
a.渡船问题的分解
b.拉绳问题的分解
4.运动的分解
合运动与分运动
【例1】关于互成角度的两个初速度不为0的匀变速直线运动的合运动,下述说法正确的是( )
A.一定是直线运动
B.一定是抛物线运动
C.可能是直线运动,也可能是抛物线运动
D.以上说法都不对
C
2.关于运动的合成,下列说法中正确的( )
A.合运动的速度一定比每一个分运动的速度大
B.两个分运动的时间一定与它们合运动的时间相等
C.只要两个分运动是直线运动,合运动一定是直线运动
D.两个匀变速直线运动的合运动一定是匀变速直线运动
B
例1:一艘小船在100m宽的河中横渡到对岸,已知水流速度是3m/s,小船在静水中的速度是4m/s,求:
欲使船渡河时间最短,船应该怎样渡河?最短时间是多少?船经过的位移多大?
运动的合成和分解的应用:小船渡河
分析1:时间最短
d
结论:欲使船渡河时间最短,船头的方向应该垂直于河岸。
解1:当船头垂直河岸时,所用时间最短
最短时间
此时合速度
此时航程
例2:一艘小船在100m宽的河中横渡到对岸,已知水流速度是3m/s,小船在静水中的速度是4m/s,求:
欲使航行距离最短,船应该怎样渡河?渡河时间多长?
分析2:航程最短
θ
d
设船头指向与上游河岸成θ:
结论:当v船>v水时,最短航程等于河宽d。
解:2、当船头指向斜上游,与岸夹角为?时,合运动垂直河岸,航程最短,数值等于河宽100米。
过河时间:
合速度:
则cos ? =
小船过河
假如船不动 水流动
V水
小船过河
假如水不流动 船动
V船
小船过河问题
V水
V船
小船过河问题
V水
V船
问题拓展
1、在船头始终垂直对岸的情况下,在行驶到河中间时,水流速度突然增大,过河时间如何变化?
2、为了垂直到达河对岸,在行驶到河中间时,水流速度突然增大,过河时间如何变化?
答案:变长
答案:不变
【例题】如图所示,纤绳以恒定速率v沿水平方向通过定滑轮牵引小船靠岸,当纤绳与水面夹角为θ时,船靠岸的速度是 ,若使船匀速靠岸,则纤绳的速度是 。(填:匀速、加速、减速)
减速
运动的合成和分解的应用:绳物模型
注:物体的实际运动为合运动
练习如图所示,汽车沿水平路面以恒定速度v前进,则当拉绳与水平方向成θ角时,被吊起的物体M的速度为vM= 。
【答案】
选做:若河宽仍为100m,已知水流速度是4m/s,小船在静水中的速度是3m/s,即船速(静水中)小于水速。
求:
(1)欲使船渡河时间最短,船应该怎样渡河?
(2)欲使航行距离最短,船应该怎样渡河?最短航线是河宽吗?
θ
θ
结论:当v船< v水时,最短航程不等于河宽d。
船头指向与上游河岸成θ:
小结
探究曲线运动的基本方法——运动的合成与分解.这种方法在应用过程中遵循平行四边形定则.在实际的解题过程中,通常选择实际看到的运动为合运动,其他的运动为分运动.运动的合成与分解包括以下几方面的内容:
(1)速度的合成与分解;
(2)位移的合成与分解;
(3)加速度的合成与分解.
合运动与分运动之间还存在如下的特点:
独立性;等效性;等时性
