苏科版八下数学第12章二次根式考点 易错整理学案
文档属性
| 名称 | 苏科版八下数学第12章二次根式考点 易错整理学案 |  | |
| 格式 | zip | ||
| 文件大小 | 579.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-18 09:58:10 | ||
图片预览



文档简介
第12章《二次根式》考点+易错整理
知识梳理
重难点分类解析
考点1 二次根式的概念和性质
【考点解读】一般地,式子叫做二次根式,叫做被开方数,被开方数为非负数.这是中考重要考点之一.二次根式的性质是二次根式化简计算的依据,其性质有两个:一是当时,;二是.在中考中多以计算的形式出现在选择题或填空题中.
例1 (2018·苏州)若在实数范围内有意义,则的取值范围在数轴上表示正确的是( )
分析:由题意,得,解得.在数轴上表示是在点-2处取向右的方向,-2处用实心点圆.
答案:D
【规律·技法】要使一个代数式有意义,在确定字母的取值范围时,若含有分式,则分母不为0;若含有二次根式,则被开方数为非负数.
【反馈练习】
1.若有意义,则实数的取值范围是( )
A. B. C. D.
点拨:二次根式的被开方数大于或等于0,且分母不为零.
2.已知实数在数轴上对应点的位置如图所示,则化简的结果是( )
A. B. C. 3 D.-3
点拨:由数轴可知与的符号,从而进行化简.
考点2 二次根式的乘除
【考点解读】二次根式的乘除主要运算公式有,这两个公式是将二次根式进行化简计算的依据,二次根式化简后要求化为最简二次根式,即被开方数中不含能开得尽方的因数或因式,被开方数中不含分母,分母中不含根式.中考中本知识点常以选择题形式出现.
例2 下列式子为最简二次根式的是( )
A. B. C. D.
分析:A.被开方数不含分母,被开方数不含能开得尽方的因数或因式,故A符合题意;B.被开方数含能开得尽方的因数,故B不符合题意;C.被开方数含能开得尽方的因数,故C不符合题意;D。被开方数含分母,故D不符合题意.
答案:A
【规律·技法】最简二次根式必须满足三个条件:被开方数中不含能开得尽方的因数或因式;被开方数中不含分母;分母中不含有根号.
【反馈练习】
3. (2018·镇江) = .
点拨:利用二次根式的乘法法则可得.
4.下列各式中,错误的是( )
A. B. C. D.
点拨:利用二次根式的性质和乘除法则求解.
考点3 二次根式的加减
【考点解读】二次根式的加减运算的本质即为二次根式的化简,然后合并同类二次根式.进行二次根式混合运算时,整式运算的法则、公式和运算律仍然适用.中考主要以简单的计算题为主,属于简单题型.
例3 计算: = .
分析:原式=.
答案:
【规律·技法】二次根式的混合运算,先把各二次根式化为最简二次根式,再进行二次根式的加减运算,最后合并同类二次根式.
【反馈练习】
5.计算:
(1) ; (2) .
点拨:利用二次根式的性质和混合运算法则求解.
6.计算:
(1) ; (2) .
点拨:利用二次根式的运算法则求解.
考点4 二次根式的化简求值
【考点解读】二次根式的化简求值,主要利用二次根式的性质及运算法则.中考要求较低,一般以选择题或填空题的形式出现.
例4 已知,则的值为( )
A.2 B. 4 C. 5 D. 7
分析:
答案:B
【规律·技法】二次根式的化简求值,熟知二次根式混合运算的法则是解答此题的关键.
【反馈练习】
7.如果为有理数),那么等于( )
A. B. 8 C. D. 10
点拨:由二次根式的乘法运算求解.
8.已知,求代数式的值.
点拨:先分别对分母有理化,再代入求解.
考点5 二次根式的应用
【考点解读】二次根式的应用比较广泛,有关数学类计算均可涉及,应用过程主要体现二次根式的化简与计算过程,难度比较低,属于简单的计算题.
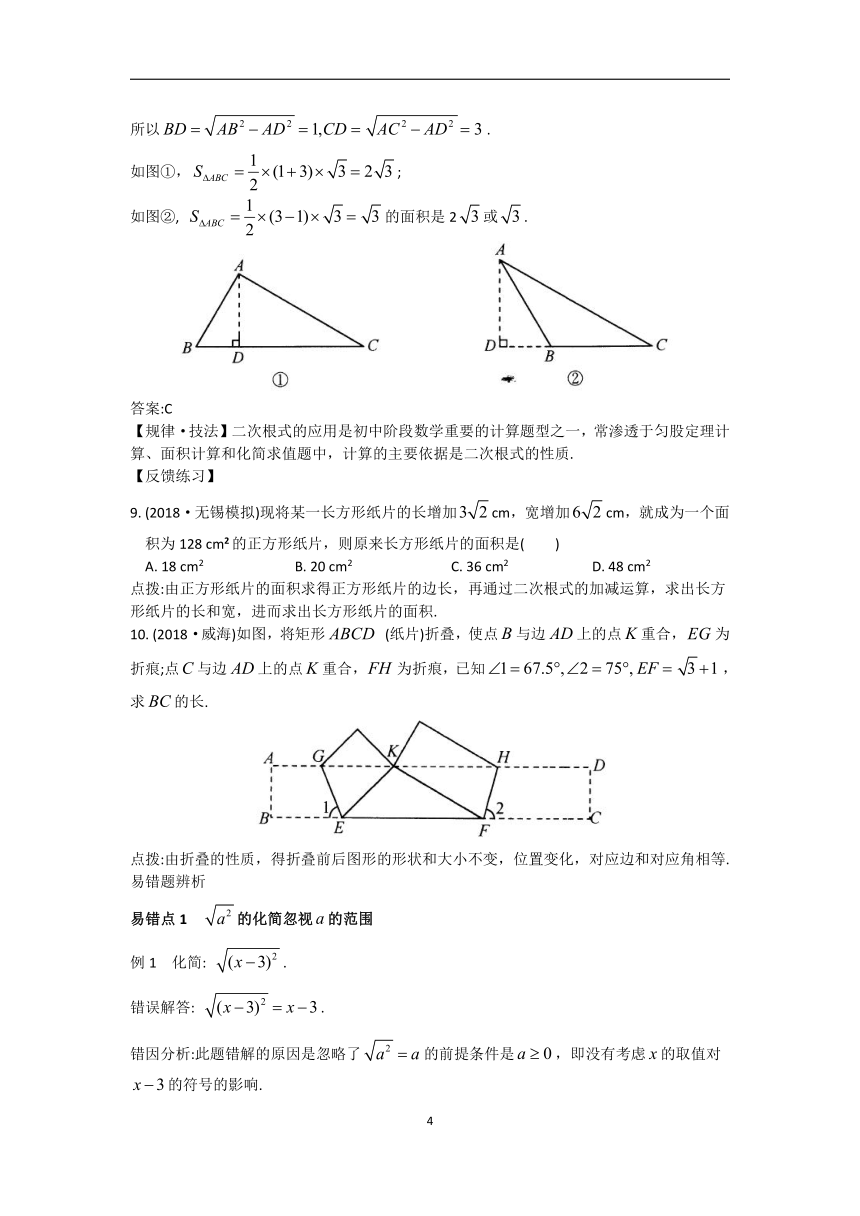
例5 已知的两边长和分别为2和,且第三边上的高等于,则的面积是( )
A. B. 2 C. 或2 D.不能确定
分析:由题意,得.
所以.
如图①,;
如图②, 的面积是2或.
答案:C
【规律·技法】二次根式的应用是初中阶段数学重要的计算题型之一,常渗透于匀股定理计算、面积计算和化简求值题中,计算的主要依据是二次根式的性质.
【反馈练习】
9. (2018·无锡模拟)现将某一长方形纸片的长增加cm,宽增加cm,就成为一个面
积为128 cm2的正方形纸片,则原来长方形纸片的面积是( )
A. 18 cm2 B. 20 cm2 C. 36 cm2 D. 48 cm2
点拨:由正方形纸片的面积求得正方形纸片的边长,再通过二次根式的加减运算,求出长方形纸片的长和宽,进而求出长方形纸片的面积.
10. (2018·威海)如图,将矩形 (纸片)折叠,使点与边上的点重合,为
折痕;点与边上的点重合,为折痕,已知,求的长.
点拨:由折叠的性质,得折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
易错题辨析
易错点1 的化简忽视的范围
例1 化简: .
错误解答: .
错因分析:此题错解的原因是忽略了的前提条件是,即没有考虑的取值对的符号的影响.
正确解答: =.
易错辨析:在对进行化简时,由于的取值为任意实数,先得到,再根据的取值情况进行讨论,而不能误认为.
易错点2 运算顺序不正确
例2 计算:
(1) ;
(2) ;
(3).
错误解答:(1) .
(2) .
(3) .
错因分析:本题错在没有正确掌握二次根式混合运算的顺序.
正确解答:(1).
(2) .
(3) .
易错辨析:二次根式混合运算的顺序与有理数混合运算的顺序相同,都是先乘方,再乘除,最后加减,有括号则先算括号内的.
【反馈练习】
1.化简:
(1) ; (2).
点拨:不能忽视算术平方根的非负性
2.计算:
(1) ; (2) .
点拨:利用运算法则进行计算时,应看清运算顺序.
探究与应用
探究1 整体代换求值
例1 已知,求的值.
点拨:由求值式变形: ,需先将分母有理化,再求出的值,然后整体代入就可以计算了.
解答:因为,所以.所以.
【规律·提示】先分母有理化,再代入计算即可.
【举一反三】
1.已知,求代数式的
值.
探究2 值的估算
例2 已知实数的整数部分为,小数部分为,求的值.
点拨:对于实数,可写为,其中表示的整数部分,表示的小数部分,且,如.由此知识先确定的整数部分和小数部分,再代入求值.
解答:由题意,得.因为,所以,所以整部分,即,所以小数部分.所以.
【规律·提示】先分别表示出的值,再代入求值.
例3 不用计算器,试比较和的大小.
点拨: 与互为倒数,与为倒数,通过变形,使之成为同分子的分数相比较.
解答:方法一:因为,所以.因为,所以.因为,所以,所以.
方法二:(作差比较)因为,且,,所以,所以.
【规律·提示】“数感”是课程标准的一个重要教学目标,实数作为二次根式运算的一部分内容,在培养运算能力中成为一个重要的载体.
【举一反三】
2. (1)化简:;
(2)设为的小数部分,为的小数部分,求的值.
3.公元三世纪,我国古代数学家刘徽就能利用近似公式得到的近似值.他的算法是:先看成,由近似公式得到;再看成了,由近似公式得到,……,依此算法,所得的近似值会越来越精确.当取得近似值时,试确定近似公式中的与的值
参考答案
知识梳理
合并同类二次根式 仍适用于
重难点分类解析
【反馈练习】
1. B 2. C
3. 2
4. B
5. (1)
(2)
6.(1)
(2)
7. D
8.
9. B
10.
易错题辨析
【反馈练习】
1. (1)
(2)
2. (1)
(2)
探究与应用
【举一反三】
1.
当时,原式
2. (1)
(2)
3.
3
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
