北师大版高中数学选修2-2第三章 2.2最大值、最小值问题 导数与函数的最值 课件(28张ppt)
文档属性
| 名称 | 北师大版高中数学选修2-2第三章 2.2最大值、最小值问题 导数与函数的最值 课件(28张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-18 10:58:11 | ||
图片预览





文档简介
(共28张PPT)
*
北师大版高中数学选修2-2第三章《导数应用》
*
一、教学目标:1、知识与技能:会求函数的最大值与最小值。2、过程与方法:通过具体实例的分析,会利用导数求函数的最值。3、情感、态度与价值观:让学生感悟由具体到抽象,由特殊到一般的思想方法。
二、教学重点:函数最大值与最小值的求法 教学难点:函数最大值与最小值的求法
三、教学方法:探究归纳,讲练结合
四、教学过程:
*
必要条件
(一)、知识回顾:
*
f(a)
f(b)
极大值点和极小值点
统称为极值点
极大值和极小值
统称为极值
函数极值的判定定理
x xb
f ’(x) + 0 -
f(x) 单调
递增 极大值 单调
递减
x xa
f ’(x) - 0 +
f(x) 单调
递减 极小值 单调
递增
*
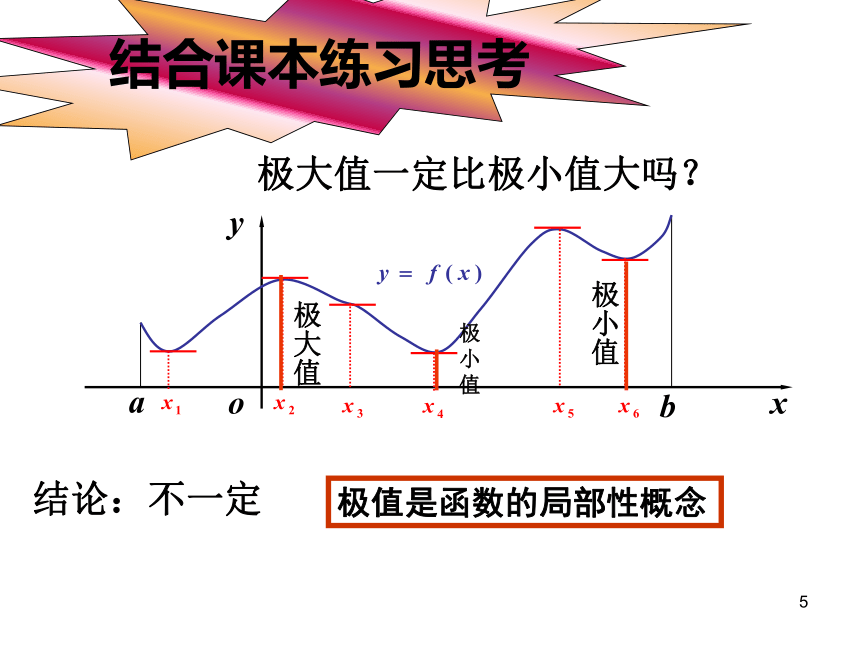
结合课本练习思考
极大值一定比极小值大吗?
极值是函数的局部性概念
结论:不一定
极大值
极小值
极小值
*
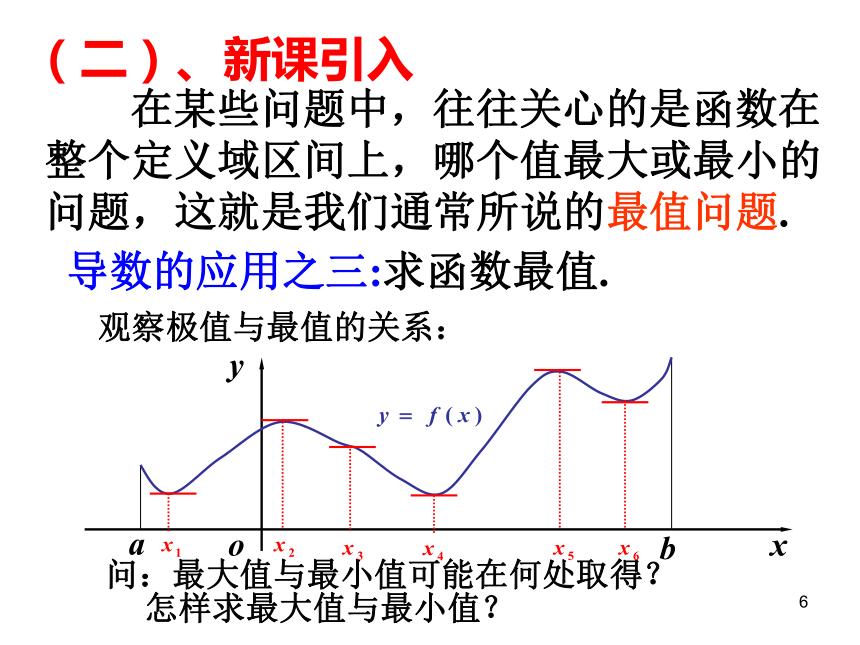
导数的应用之三:求函数最值.
在某些问题中,往往关心的是函数在整个定义域区间上,哪个值最大或最小的问题,这就是我们通常所说的最值问题.
(二)、新课引入
问:最大值与最小值可能在何处取得?
怎样求最大值与最小值?
观察极值与最值的关系:
*
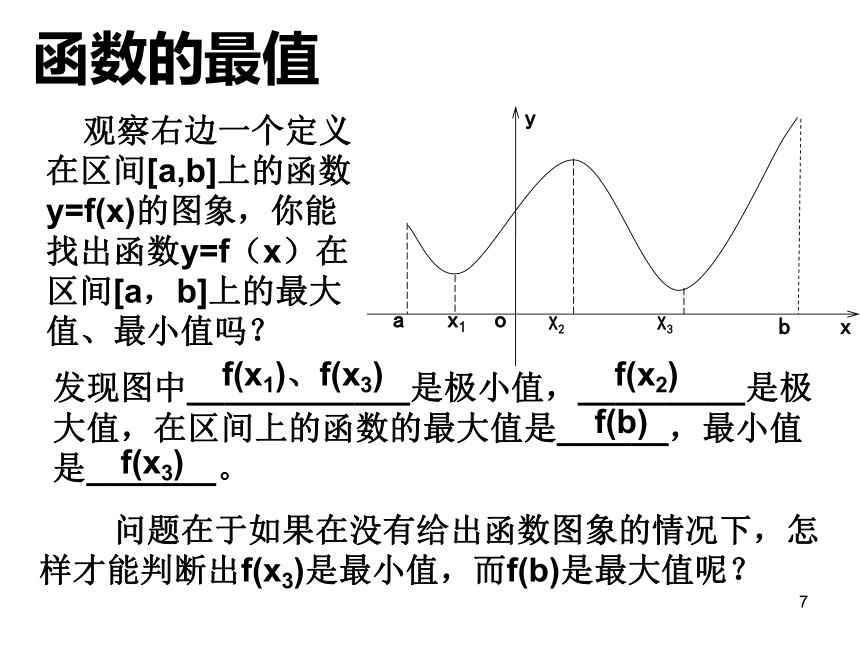
函数的最值
观察右边一个定义在区间[a,b]上的函数y=f(x)的图象,你能找出函数y=f(x)在区间[a,b]上的最大值、最小值吗?
发现图中____________是极小值,_________是极大值,在区间上的函数的最大值是______,最小值是_______。
问题在于如果在没有给出函数图象的情况下,怎样才能判断出f(x3)是最小值,而f(b)是最大值呢?
*
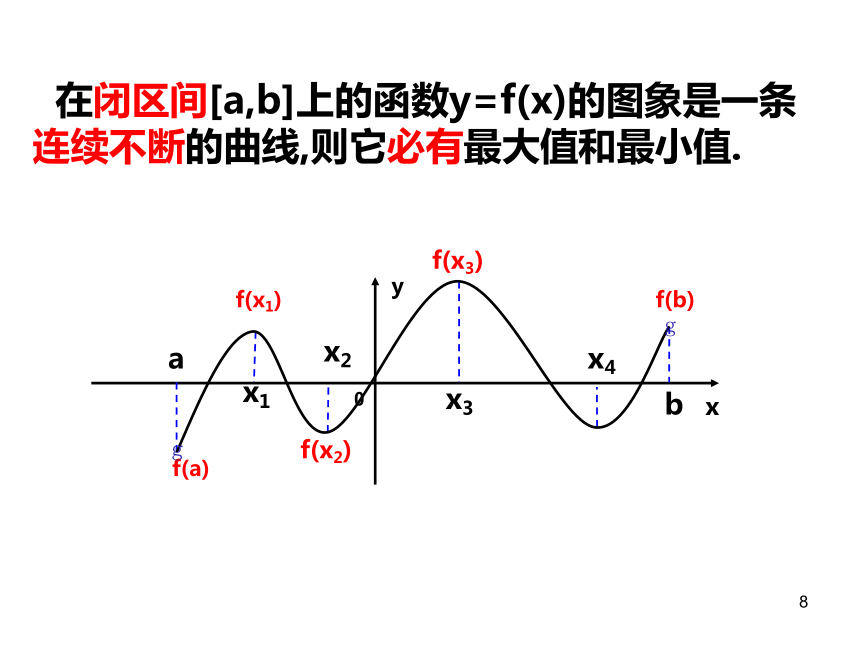
在闭区间[a,b]上的函数y=f(x)的图象是一条连续不断的曲线,则它必有最大值和最小值.
*
(2)将y=f(x)的各极值与f(a)、f(b)比较,其中最大的一个为最大值,最小的一个最小值
求f(x)在闭区间[a,b]上的最值的步骤:
(1)求f(x)在区间(a,b)内极值(极大值或极小值)
(三)、新课探析:
求函数的最值时,应注意以下几点:
(1)函数的极值是在局部范围内讨论问题,是一个局部概
念,而函数的最值是对整个定义域而言,是在整体范围
内讨论问题,是一个整体性的概念.
(2)闭区间[a,b]上的连续函数一定有最值.开区间(a,b)内
的可导函数不一定有最值,但若有唯一的极值,则此极
值必是函数的最值.
*
(3)函数在其定义域上的最大值与最小值至多各有一个,而函数的极值则可能不止一个,也可能没有极值,并且极大值(极小值)不一定就是最大值(最小值),但除端点外在区间内部的最大值(或最小值),则一定是极大值(或极小值).
(4)如果函数不在闭区间[a,b]上可导,则在确定函数的最值时,不仅比较该函数各导数为零的点与端点处的值,还要比较函数在定义域内各不可导的点处的值.
*
o
x
y
a
b
o
x
y
a
b
o
x
y
a
b
o
x
y
a
b
y=f(x)
y=f(x)
y=f(x)
y=f(x)
在闭区间上的连续函数必有最大值与最小值,
在开区间内的连续函数不一定有最大值与
最小值.
*
例1、求函数f(x)=x2-4x+6在区间[1,5]内
的最大值和最小值.
法一 、 将二次函数f(x)=x2-4x+6配方,利用二次函数单调性处理
(四)、知识运用:
一是利用函数性质;二是利用不等式;三是利用导数。
注:
求函数最值的一般方法:
*
例1、求函数f(x)=x2-4x+6在区间[1,5]内
的极值与最值
故函数f(x) 在区间[1,5]内有极小值为2,
最大值为11,最小值为2
法二、
解、 f ’(x)=2x-4
令f ’(x)=0,即2x-4=0,
得x=2。
-
+
3
11
2
x 1 (1,2) 2 (2,5) 5
y/
0
y
*
如果函数 f (x)在[a, b]上单调增加(减少),
则 f (a)是 f(x)在[a, b]上的最小值(最大值),f (b)
是 f (x)在[a, b]上的最大值(最小值)。
函数的最值一般有两种情况:
(1)
*
如果函数在区间(a, b)内有且仅有一个极大(小)值,而没有极小(大)值,则此极大(小)值就是函数在区间[a, b]上的最大(小)值。
函数的最值一般分为两种情况:
(2)如果函数在区间(a, b)内有极值,将y=f(x)的各极值与f(a)、f(b)比较,其中最大的一个为最大值,最小的一个最小值.
*
求函数在闭区间内的最值的步骤
求出函数 y = f (x)在(a , b)内的全部驻点和
驻点处的函数值;
(2) 求出区间端点处的函数值;
比较以上各函数值,其中最大的就是函数
的最大值,最小的就是函数的最小值。
例1:求
↘
-4/3
+
在[0,3]的最大值与最小值
4
-
0
↗
1
因此,函数在[0,3]上的最大值是4,
最小值是- 4/3.
三、例题讲解
-
+
x 0 (0,2) 2 (2,3) 3
y′
y
*
求下列函数在指定区间内的最大值和最小值。
最大值 f (1)=-29,最小值 f (3)= -61
课堂练习:
*
1. 求 在 上的最大值与最小值的步骤:
小结
2.求函数最值的一般方法:①.是利用函数性质;②.是利用不等式;③.是利用导数
*
北师大版高中数学选修2-2第三章《导数应用》
*
一、教学目标:1、知识与技能:会求函数的最大值与最小值。2、过程与方法:通过具体实例的分析,会利用导数求函数的最值。3、情感、态度与价值观:让学生感悟由具体到抽象,由特殊到一般的思想方法。
二、教学重点:函数最大值与最小值的求法 教学难点:函数最大值与最小值的求法
三、教学方法:探究归纳,讲练结合
四、教学过程:
*
必要条件
(一)、知识回顾:
*
f(a)
f(b)
极大值点和极小值点
统称为极值点
极大值和极小值
统称为极值
函数极值的判定定理
x xb
f ’(x) + 0 -
f(x) 单调
递增 极大值 单调
递减
x xa
f ’(x) - 0 +
f(x) 单调
递减 极小值 单调
递增
*
结合课本练习思考
极大值一定比极小值大吗?
极值是函数的局部性概念
结论:不一定
极大值
极小值
极小值
*
导数的应用之三:求函数最值.
在某些问题中,往往关心的是函数在整个定义域区间上,哪个值最大或最小的问题,这就是我们通常所说的最值问题.
(二)、新课引入
问:最大值与最小值可能在何处取得?
怎样求最大值与最小值?
观察极值与最值的关系:
*
函数的最值
观察右边一个定义在区间[a,b]上的函数y=f(x)的图象,你能找出函数y=f(x)在区间[a,b]上的最大值、最小值吗?
发现图中____________是极小值,_________是极大值,在区间上的函数的最大值是______,最小值是_______。
问题在于如果在没有给出函数图象的情况下,怎样才能判断出f(x3)是最小值,而f(b)是最大值呢?
*
在闭区间[a,b]上的函数y=f(x)的图象是一条连续不断的曲线,则它必有最大值和最小值.
*
(2)将y=f(x)的各极值与f(a)、f(b)比较,其中最大的一个为最大值,最小的一个最小值
求f(x)在闭区间[a,b]上的最值的步骤:
(1)求f(x)在区间(a,b)内极值(极大值或极小值)
(三)、新课探析:
求函数的最值时,应注意以下几点:
(1)函数的极值是在局部范围内讨论问题,是一个局部概
念,而函数的最值是对整个定义域而言,是在整体范围
内讨论问题,是一个整体性的概念.
(2)闭区间[a,b]上的连续函数一定有最值.开区间(a,b)内
的可导函数不一定有最值,但若有唯一的极值,则此极
值必是函数的最值.
*
(3)函数在其定义域上的最大值与最小值至多各有一个,而函数的极值则可能不止一个,也可能没有极值,并且极大值(极小值)不一定就是最大值(最小值),但除端点外在区间内部的最大值(或最小值),则一定是极大值(或极小值).
(4)如果函数不在闭区间[a,b]上可导,则在确定函数的最值时,不仅比较该函数各导数为零的点与端点处的值,还要比较函数在定义域内各不可导的点处的值.
*
o
x
y
a
b
o
x
y
a
b
o
x
y
a
b
o
x
y
a
b
y=f(x)
y=f(x)
y=f(x)
y=f(x)
在闭区间上的连续函数必有最大值与最小值,
在开区间内的连续函数不一定有最大值与
最小值.
*
例1、求函数f(x)=x2-4x+6在区间[1,5]内
的最大值和最小值.
法一 、 将二次函数f(x)=x2-4x+6配方,利用二次函数单调性处理
(四)、知识运用:
一是利用函数性质;二是利用不等式;三是利用导数。
注:
求函数最值的一般方法:
*
例1、求函数f(x)=x2-4x+6在区间[1,5]内
的极值与最值
故函数f(x) 在区间[1,5]内有极小值为2,
最大值为11,最小值为2
法二、
解、 f ’(x)=2x-4
令f ’(x)=0,即2x-4=0,
得x=2。
-
+
3
11
2
x 1 (1,2) 2 (2,5) 5
y/
0
y
*
如果函数 f (x)在[a, b]上单调增加(减少),
则 f (a)是 f(x)在[a, b]上的最小值(最大值),f (b)
是 f (x)在[a, b]上的最大值(最小值)。
函数的最值一般有两种情况:
(1)
*
如果函数在区间(a, b)内有且仅有一个极大(小)值,而没有极小(大)值,则此极大(小)值就是函数在区间[a, b]上的最大(小)值。
函数的最值一般分为两种情况:
(2)如果函数在区间(a, b)内有极值,将y=f(x)的各极值与f(a)、f(b)比较,其中最大的一个为最大值,最小的一个最小值.
*
求函数在闭区间内的最值的步骤
求出函数 y = f (x)在(a , b)内的全部驻点和
驻点处的函数值;
(2) 求出区间端点处的函数值;
比较以上各函数值,其中最大的就是函数
的最大值,最小的就是函数的最小值。
例1:求
↘
-4/3
+
在[0,3]的最大值与最小值
4
-
0
↗
1
因此,函数在[0,3]上的最大值是4,
最小值是- 4/3.
三、例题讲解
-
+
x 0 (0,2) 2 (2,3) 3
y′
y
*
求下列函数在指定区间内的最大值和最小值。
最大值 f (1)=-29,最小值 f (3)= -61
课堂练习:
*
1. 求 在 上的最大值与最小值的步骤:
小结
2.求函数最值的一般方法:①.是利用函数性质;②.是利用不等式;③.是利用导数
同课章节目录
