鲁教版(五四制)九年级下册5.5 确定圆的条件(1) 课件(21张PPT)
文档属性
| 名称 | 鲁教版(五四制)九年级下册5.5 确定圆的条件(1) 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 763.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-18 00:00:00 | ||
图片预览







文档简介
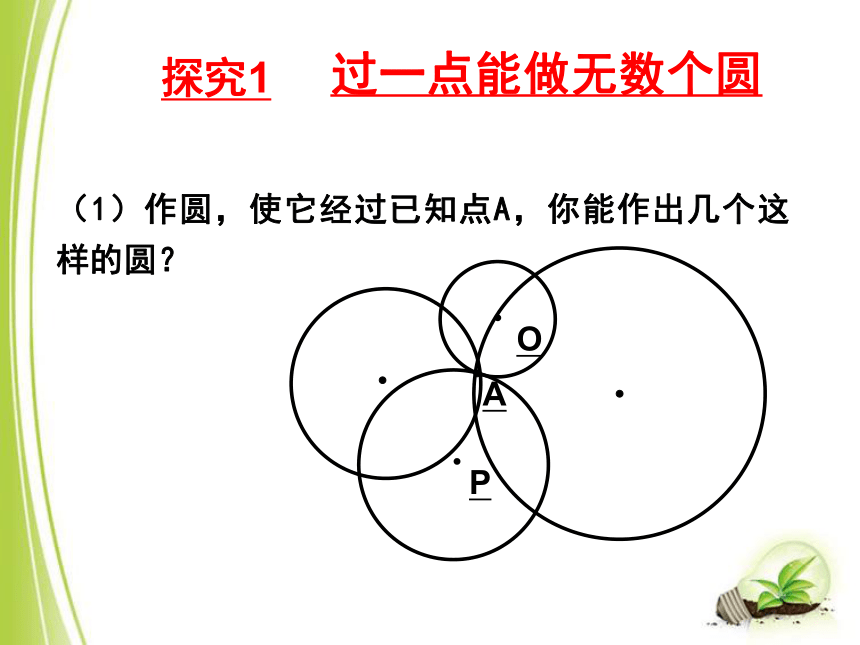
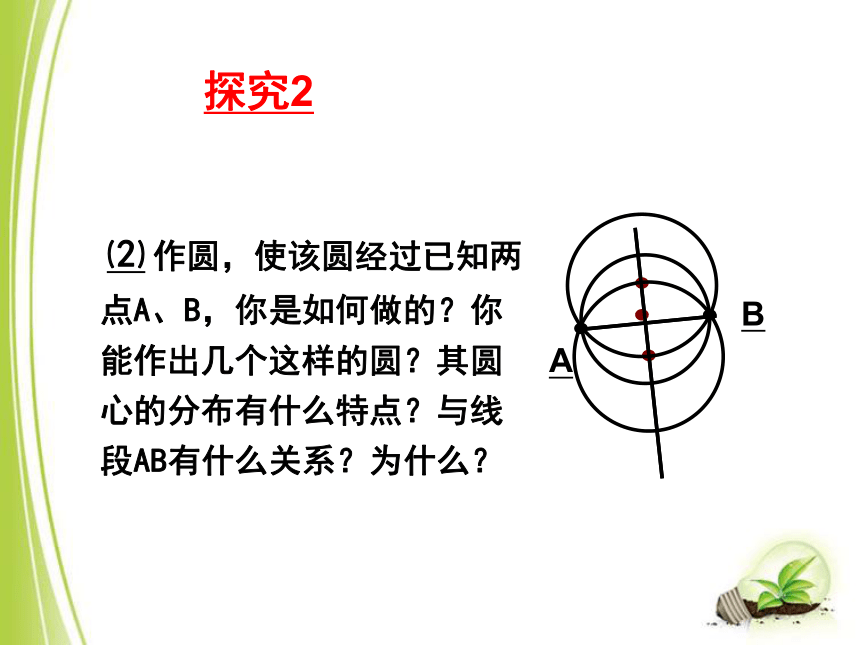
课件21张PPT。确定圆的条件(1)(1)作圆,使它经过已知点A,你能作出几个这样的圆?过一点能做无数个圆A探究1 作圆,使该圆经过已知两点A、B,你是如何做的?你能作出几个这样的圆?其圆心的分布有什么特点?与线段AB有什么关系?为什么?⑵AB探究2 经过两点能做无数个圆,且这些圆的圆心都在这两点所连线段的垂直平分线上.过已知点作圆的关键是什么?
所作圆的个数取决于什么?关键是确定圆心的位置和半径的大小;
所作圆的个数取决于圆心的位置和圆心的个数.思考1.2. 作圆,使该圆经过已知点A,B,C
(A,B,C三点不在同一条直线上)
⑶探究3你是如何做的?你能作出几个这样的圆?1.连接AB,BC.2.分别作线段AB,BC的垂直平分线DE和FG,
DE与FG相交于点O.3.以O为圆心,OA长为半径作圆.
就是所要求作的圆.CABODEFG作 法:不在同一条直线上的 三个点确定一个圆 经过三角形的三个顶点可以作一个圆,
这个圆叫做三角形的外接圆.
再获新知外接圆的圆心是三角形三边垂直平分线的交点,叫做这个三角形的外心.等腰三角形的外心一定在它的外部B选一选随堂练习1三条高的交点2.三角形的外心是( )三条边垂直平分线的交点三条中线的交点三条角平分线的交点A.D.C.B.C 已知下面三个三角形,分别作出它们的外接圆.它们外心的位置有怎样的特点?随堂练习2 锐角三角形的外心在三角形内部;
直角三角形的外心在三角形的斜边上;
钝角三角形的外心在三角形外部. 及时总结 草原上有三个放牧点,要修建一个牧民定居点,
使得三个放牧点到定居点的距离相等.随堂练习3(1)如果三个放牧点的位置如下图所示,
那么如何确定定居点的位置?放牧点1放牧点2放牧点3定居点如果另外一处草原上也有三个放牧点,那么满足同样条件的定居点的位置应设在何处?(2) 定居点放牧点1放牧点2放牧点3 已知AB=4cm,以3cm长为半径作圆,使它经过点A 和点B.这样的圆能作几个? AB1.数学理解如图,MN所在的直线垂直平分线段AB,利用这样的工具,最少使用多少次, 就可以确定圆形工件的圆心?2.ABMN为什么?本节课你收获了什么?1.确定圆的条件:2.三角形的外接圆: 经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆.
不在同一条直线上的三个点确定一个圆3.三角形的外心:外接圆的圆心是三角形三边垂直平分
线的交点,叫做这个三角形的外心.知
识
技
能数学思想 转化、类比、
数学建模等思想
所作圆的个数取决于什么?关键是确定圆心的位置和半径的大小;
所作圆的个数取决于圆心的位置和圆心的个数.思考1.2. 作圆,使该圆经过已知点A,B,C
(A,B,C三点不在同一条直线上)
⑶探究3你是如何做的?你能作出几个这样的圆?1.连接AB,BC.2.分别作线段AB,BC的垂直平分线DE和FG,
DE与FG相交于点O.3.以O为圆心,OA长为半径作圆.
就是所要求作的圆.CABODEFG作 法:不在同一条直线上的 三个点确定一个圆 经过三角形的三个顶点可以作一个圆,
这个圆叫做三角形的外接圆.
再获新知外接圆的圆心是三角形三边垂直平分线的交点,叫做这个三角形的外心.等腰三角形的外心一定在它的外部B选一选随堂练习1三条高的交点2.三角形的外心是( )三条边垂直平分线的交点三条中线的交点三条角平分线的交点A.D.C.B.C 已知下面三个三角形,分别作出它们的外接圆.它们外心的位置有怎样的特点?随堂练习2 锐角三角形的外心在三角形内部;
直角三角形的外心在三角形的斜边上;
钝角三角形的外心在三角形外部. 及时总结 草原上有三个放牧点,要修建一个牧民定居点,
使得三个放牧点到定居点的距离相等.随堂练习3(1)如果三个放牧点的位置如下图所示,
那么如何确定定居点的位置?放牧点1放牧点2放牧点3定居点如果另外一处草原上也有三个放牧点,那么满足同样条件的定居点的位置应设在何处?(2) 定居点放牧点1放牧点2放牧点3 已知AB=4cm,以3cm长为半径作圆,使它经过点A 和点B.这样的圆能作几个? AB1.数学理解如图,MN所在的直线垂直平分线段AB,利用这样的工具,最少使用多少次, 就可以确定圆形工件的圆心?2.ABMN为什么?本节课你收获了什么?1.确定圆的条件:2.三角形的外接圆: 经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆.
不在同一条直线上的三个点确定一个圆3.三角形的外心:外接圆的圆心是三角形三边垂直平分
线的交点,叫做这个三角形的外心.知
识
技
能数学思想 转化、类比、
数学建模等思想
