鲁教版(五四制)九年级下册5.6 直线和圆的位置关系 (1) 课件(21张PPT)
文档属性
| 名称 | 鲁教版(五四制)九年级下册5.6 直线和圆的位置关系 (1) 课件(21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 816.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-18 21:49:51 | ||
图片预览






文档简介
课件21张PPT。直线和圆的位置关系(1) 直线和圆有两个公共点,
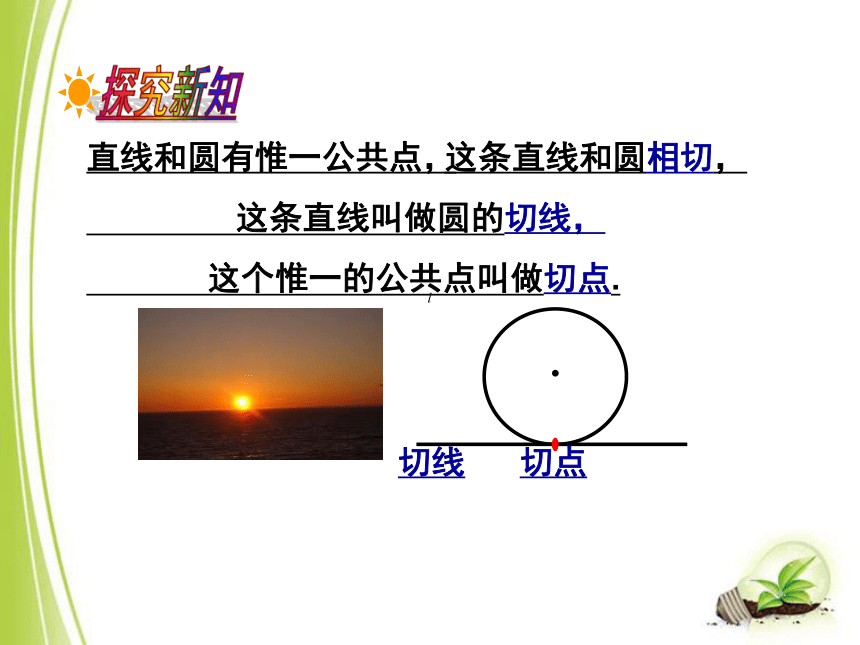
这条直线和圆相交.直线和圆有惟一公共点,
这条直线叫做圆的切线,
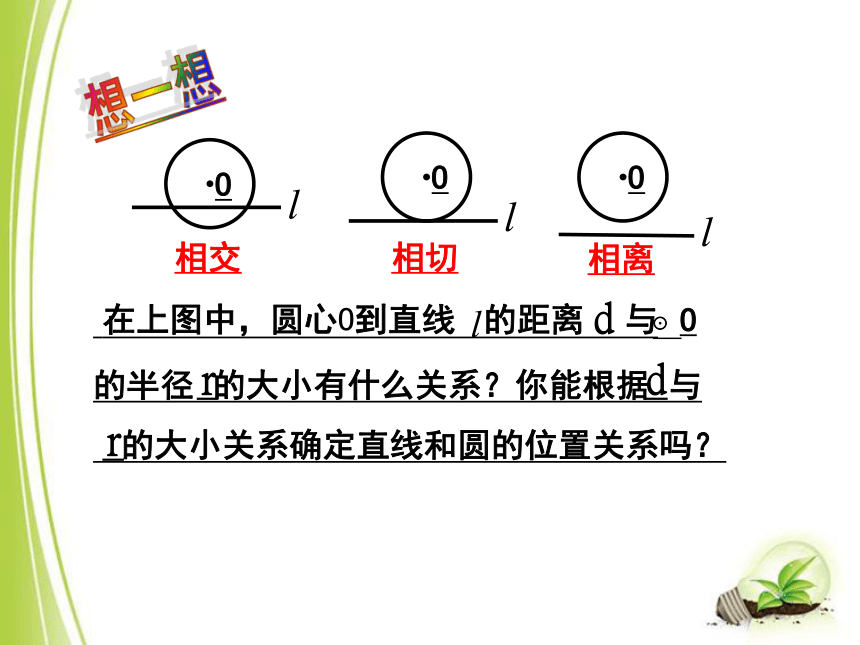
这个惟一的公共点叫做切点.切线切点这条直线和圆相切,直线和圆没有公共点,这条直线和圆相离.想一想相交相切相离点与圆的关系:点在圆内,即d<r.点在圆上,即d=r.点在圆外,即d>r.知识链接O直线和圆相交,即 rdd r<及时总结Ord直线和圆相切,即 d r=及时总结Ord直线和圆相离,即 d r>及时总结知识汇总议一议你能举出生活中直线和圆相交、相切、相离的实例吗?与同伴进行交流.典型例题例1:如图,在Rt△ABC中∠C= 90°,AB=8cm,AC=4cm.ABC(2)以C为圆心,分别以2cm和4cm 的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系? (1)以C为圆心作圆,当半径的长为多少时,AB与⊙C相切?解: (1)如图,过点C作CD⊥AB,垂足为D, 在Rt△ABC中,(2)由(1)可知,圆心C到AB的距离d= cm,所以,
当r=2cm时, d>r , ⊙C和AB相离;
当r=3cm时, d∵ AC=4cm, AB=8cm,∴∴ ∠A=60°.∴因此,当半径的长为 cm时, AB与⊙C相切.ABCD对于例1(1),你还有其他解法吗?1.已知一条直线 与半径为r的⊙O相交,且点O到直线 的距离为5,求r的取值范围.∴ d < r ∴ r > 55如图,一艘渔船正由西向东追赶鱼群,在A处测得小岛C在船的北偏东60°方向,距A处80海里,此时渔船得到通知,以小岛C为中心周围30海里以内为我军导弹部队军事演习的着弹危险区,问这艘渔船继续向东追赶鱼群,是否有进入危险区域的可能?问题解决60°北AC东D1CD=80÷2=40>30D1解:过点C作正东方向的垂线段CD
则∠1=90°-60°=30°
∴在Rt△ACD中,
CD=AC÷2=80÷2=40(海里)
∵40>30
∴这艘渔船没有进入危险区的可能.回顾总结本节课你收获了什么?知
识
技
能1.直线和圆的位置关系数学思想数形结合思想
这条直线和圆相交.直线和圆有惟一公共点,
这条直线叫做圆的切线,
这个惟一的公共点叫做切点.切线切点这条直线和圆相切,直线和圆没有公共点,这条直线和圆相离.想一想相交相切相离点与圆的关系:点在圆内,即d<r.点在圆上,即d=r.点在圆外,即d>r.知识链接O直线和圆相交,即 rdd r<及时总结Ord直线和圆相切,即 d r=及时总结Ord直线和圆相离,即 d r>及时总结知识汇总议一议你能举出生活中直线和圆相交、相切、相离的实例吗?与同伴进行交流.典型例题例1:如图,在Rt△ABC中∠C= 90°,AB=8cm,AC=4cm.ABC(2)以C为圆心,分别以2cm和4cm 的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系? (1)以C为圆心作圆,当半径的长为多少时,AB与⊙C相切?解: (1)如图,过点C作CD⊥AB,垂足为D, 在Rt△ABC中,(2)由(1)可知,圆心C到AB的距离d= cm,所以,
当r=2cm时, d>r , ⊙C和AB相离;
当r=3cm时, d
则∠1=90°-60°=30°
∴在Rt△ACD中,
CD=AC÷2=80÷2=40(海里)
∵40>30
∴这艘渔船没有进入危险区的可能.回顾总结本节课你收获了什么?知
识
技
能1.直线和圆的位置关系数学思想数形结合思想
