苏科版七年级数学下册同步练习 :7.1 探索直线平行的条件(含答案)
文档属性
| 名称 | 苏科版七年级数学下册同步练习 :7.1 探索直线平行的条件(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 139.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-18 23:43:11 | ||
图片预览



文档简介
7.1 探索直线平行的条件
一.选择题(共10小题)
1.如图,∠1=120°,要使a∥b,则∠2的大小是( )
A.60° B.80° C.100° D.120°
2.如图,不能判定AB∥CD的是( )
A.∠B=∠DCE B.∠A=∠ACD
C.∠B+∠BCD=180° D.∠A=∠DCE
3.如图,直线a,b被直线c所截,下列条件中,不能判定a∥b( )
A.∠2=∠4 B.∠1+∠4=180° C.∠5=∠4 D.∠1=∠3
4.将一副三角板(∠A=30°,∠E=45°)按如图所示方式摆放,使得BA∥EF,则∠AOF等于( )
A.75° B.90° C.105° D.115°
5.如图,直线AD,BE被直线BF和AC所截,则∠1的同位角和∠5的内错角分别是( )
A.∠4,∠2 B.∠2,∠6 C.∠5,∠4 D.∠2,∠4
6.如图,直线a,b被直线c所截,那么∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
7.如图,已知两直线l1与l2被第三条直线l3所截,下列等式一定成立的是( )
A.∠1=∠2 B.∠2=∠3 C.∠2+∠4=180° D.∠1+∠4=180°
8.下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容
则回答正确的是( )
A.◎代表∠FEC B.@代表同位角 C.▲代表∠EFC D.※代表AB
9.如图所示,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为( )
A.∠C+∠ADC=180° B.∠A+∠ABD=180°
C.∠CBD=∠ADC D.∠C=∠CDA
10.如图,在四边形ABCD中,点E在线段DC的延长线上,能使直线AD∥BC的条件有( )(1)∠D=∠BCE,(2)∠B=∠BCE,(3)∠A+∠B=180°,(4)∠A+∠D=180°,(5)∠B=∠D
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题)
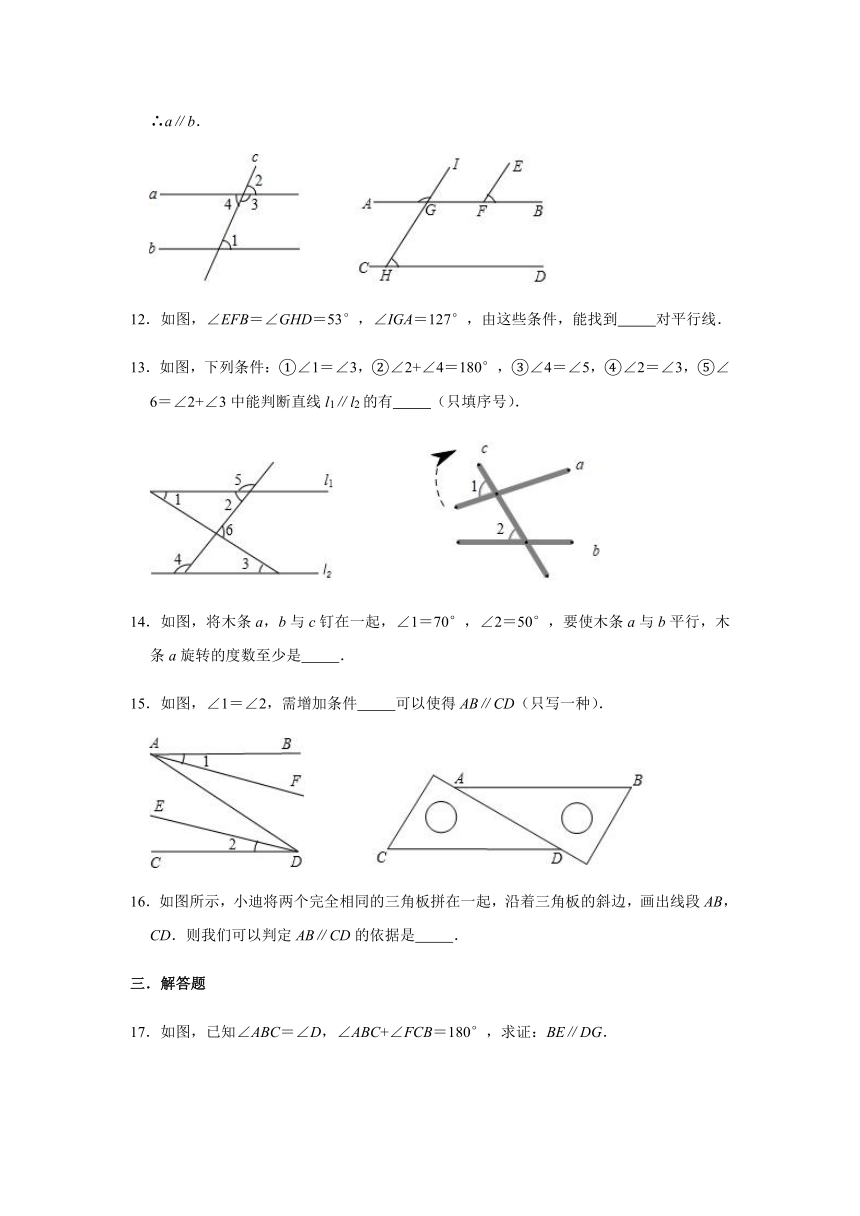
11.结合图,用符号语言表达定理“同旁内角互补,两直线平行”的推理形式:∵ ,∴a∥b.
12.如图,∠EFB=∠GHD=53°,∠IGA=127°,由这些条件,能找到 对平行线.
13.如图,下列条件:①∠1=∠3,②∠2+∠4=180°,③∠4=∠5,④∠2=∠3,⑤∠6=∠2+∠3中能判断直线l1∥l2的有 (只填序号).
14.如图,将木条a,b与c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是 .
15.如图,∠1=∠2,需增加条件 可以使得AB∥CD(只写一种).
16.如图所示,小迪将两个完全相同的三角板拼在一起,沿着三角板的斜边,画出线段AB,CD.则我们可以判定AB∥CD的依据是 .
三.解答题
17.如图,已知∠ABC=∠D,∠ABC+∠FCB=180°,求证:BE∥DG.
18.如图,∠1+∠2=180°,∠3=∠C.求证:DE∥BC.
19.如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,求证:BE∥DF.
20.已知:如图,CD⊥AB,垂足为D,点F是BC上的一点,FE⊥AB,垂足为E,且∠1=∠2,求证:DG∥BC.
答案
一.选择题(共10小题)
1.
D.
2.
D.
3.
D.
4.
A.
5.
B.
6.
C.
7.
D.
8.
C.
9.
A.
10.
B.
二.填空题
11.
∠1+∠3=180°.
12.
2.
13.
①②③⑤.
14.
20°.
15.
∠FAD=∠EDA(或AF∥DE)
16.
内错角相等两直线平行.
查平行线的判定,解题的关键是熟练掌握基本知识,属于中考常考题型.
三.解答题
17.
证明:∵∠ABC=∠D,∠ABC+∠FCB=180°(已知),
∴∠D+∠FCB=180°(等量代换),
∵∠ECD=∠FCB(对顶角相等),
∴∠D+∠ECD=180°(等量代换),
∴BE∥DG(同旁内角互补,两直线平行).
18.
解:∵∠1+∠DHE=180°,∠1+∠2=180°,
∴∠DHE=∠2,
∴DH∥AC,
∴∠3=∠AED,
又∵∠3=∠C,
∴∠C=∠AED,
∴DE∥BC.
19.
证明:∵在四边形ABCD中,∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∵BE平分∠B,DF平分∠D,
∴∠EBF+∠FDC=90°,
∵∠C=90°,
∴∠DFC+∠FDC=90°,
∴∠EBF=∠DFC,
∴BE∥DF.
20.
证明:∵FE⊥AB,CD⊥AB,
∴FE∥CD,
∴∠2=∠BCD,
∵∠1=∠2,
∴∠1=∠BCD,
∴DG∥BC.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
