鲁教版(五四制)九年级数学下册5.9 弧长及扇形的面积 教学课件(29张PPT)
文档属性
| 名称 | 鲁教版(五四制)九年级数学下册5.9 弧长及扇形的面积 教学课件(29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 625.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 00:00:00 | ||
图片预览







文档简介
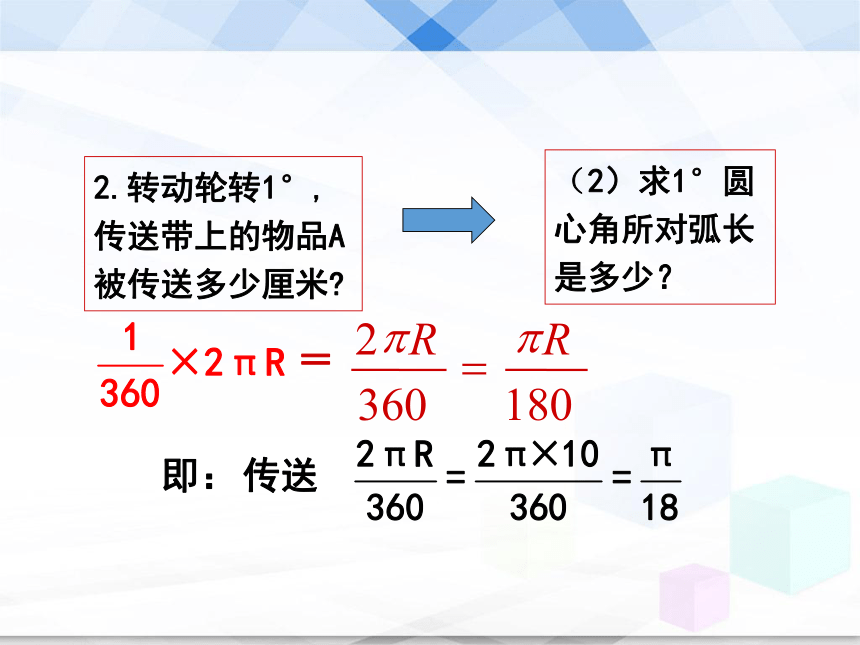
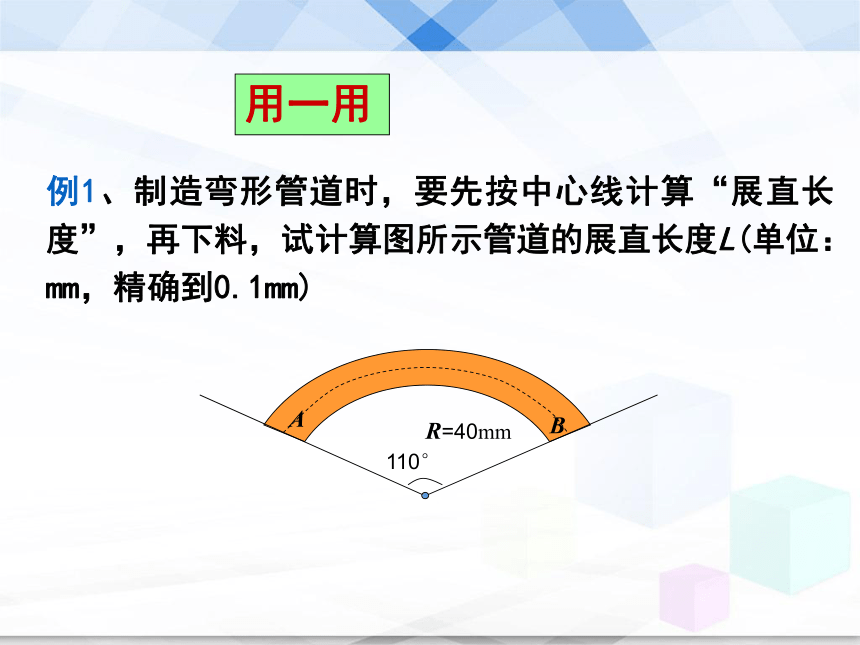
课件29张PPT。5.9 弧长及扇形的面积第五章 圆2、已知⊙O半径为R,⊙O的面积S是多少?S=πR2 C = 2πR1、已知⊙O半径为R,⊙O的周长C是多少?3、什么叫圆心角?顶点在圆心,两边和圆相交所组成的角叫做圆心角.复 习探索新知 如图,某传送带的一个转动轮的半径为10cm.1.转动轮转一周,传送带上的物品A被传送多少厘米?2.转动轮转1°,传送带上的物品A被传送多少厘米?3.转动轮转n°,传送带上的物品A被传送多少厘米?(1)求半径为R的圆,周长是多少?1.转动轮转一周,传送带上的物品A被传送多少厘米?C=2πR即:传送2π×10=20πcm问题:一个圆周可以看作是多少度的圆心角所对的弧?360°2.转动轮转1°,传送带上的物品A被传送多少厘米?(2)求1°圆心角所对弧长是多少? =即:传送3.转动轮转n°,传送带上的物品A被传送多少厘米?3.求n°的圆心角对应的弧长为多少?即:弧长公式 若设⊙O半径为R, n°的圆心角所对的弧长为l,则 (2)区分弧、弧的度数、弧长三个概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等孤,而只有在同圆或等圆中,才可能是等弧.注意 用一用 例1、制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到0.1mm)解:R=40mm, n=110,所以由弧长公式可得因此,管道的展直长度约为76.8mm.想一想在一块空旷的草地上有一根柱子,柱子上栓着一条长3m的绳子,绳子的另一端拴着一只狗.
(1)这只狗的最大活动区域有多大?
(2)如果这只狗只能绕柱子转过n°角,那么它的最大活动区域有多大?圆心角是1°的扇形面积是多少?圆心角为n°的扇形面积是多少?那么 :如果用字母 S 表示扇形的面积,圆心角为n°,R 表示圆半径,那么扇形面积的计算公式是:弧长公式与扇形的面积公式之间的联系:扇形所对的弧长扇形的面积是(2)当已知半径和圆心角的度数,求扇形面积时,应选用
温馨提示(1)当已知弧长l和半径R, 求扇形面积时,应选用弧长公式 扇形面积计算公式公式汇总用一用 例2 扇形AOB的半径为12cm,∠AOB=120°,求 的长(结果精确到0.1cm)和扇形AOB的面积(结果精确到 )解:小
练
习扇形面积大小( )
(A)只与半径长短有关
(B)只与圆心角大小有关
(C)与圆心角的大小、半径的长短有关C分析:2.一个扇形的圆心角为90o,半径为2,
则弧长= ,扇形面积= .π2π3.如果一个扇形面积是它所在圆的面积的 ,则此扇形的圆心角( )
(A)30° (B)36° (C)45° (D)60° 分析:C1.已知扇形的圆心角为120o,半径为6,则扇形的弧长是 ( )
A. 3π B.4π
C.5π D.6πB随堂练习2.圆心角为60°的一条弧长度是5π,则该弧的半径是( ) 153. 一个扇形的弧长为20πcm,面积是240πc㎡,则该扇形的圆心角为 .150o1.如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积.(精确到0.01cm)D弓形的面积= S扇- S△C求扇形面积,需要求出∠AOB
求三角形面积,需求出OD和AB巩固提高DC∵OC=0.6,DC=0.3,∴OD=OC-DC=0.3.在Rt△OAD中,OA=0.6,利用勾股定理可得,在Rt△AOD中,∴∠OAD=30°
∴ ∠AOD=60 °,∠AOB=120°解:如图,连接OA、OB,作弦AB的垂直平分线,垂足为D,交 于点C.DC有水部分的面积∵OC=0.6 OD=0.3.
∠AOB=120°2、如图,⊙A、 ⊙B、 ⊙C、 ⊙D两两不相交,且半径都是2cm,求图中阴影部分的面积。解:因为圆的半 径相同都是2厘米,四边形的内角和为360°所以3.如图,正三角形ABC的边长为a,分别以A、B 、C 为圆心,以 为半径的圆相切于点D、E、F,求图中阴影部分的面积.ABCFED解:连接AD,则垂足为D根据勾股定理,得又知,S扇形BDF=S扇形CDE=S扇形AEF,ABCFED小 结 1. 扇形的面积大小与哪些因素有关?(1)与圆心角的大小有关(2)与半径的长短有关2. 扇形面积公式与弧长公式的区别:3.在所学的公式中,存在L、R、n、S四个量,我们只要知道其中两个就可以求得其它两个.4.扇形面积单位与弧长单位的区别:(1)扇形面积单位有平方的(2)弧长单位没有平方的
(1)这只狗的最大活动区域有多大?
(2)如果这只狗只能绕柱子转过n°角,那么它的最大活动区域有多大?圆心角是1°的扇形面积是多少?圆心角为n°的扇形面积是多少?那么 :如果用字母 S 表示扇形的面积,圆心角为n°,R 表示圆半径,那么扇形面积的计算公式是:弧长公式与扇形的面积公式之间的联系:扇形所对的弧长扇形的面积是(2)当已知半径和圆心角的度数,求扇形面积时,应选用
温馨提示(1)当已知弧长l和半径R, 求扇形面积时,应选用弧长公式 扇形面积计算公式公式汇总用一用 例2 扇形AOB的半径为12cm,∠AOB=120°,求 的长(结果精确到0.1cm)和扇形AOB的面积(结果精确到 )解:小
练
习扇形面积大小( )
(A)只与半径长短有关
(B)只与圆心角大小有关
(C)与圆心角的大小、半径的长短有关C分析:2.一个扇形的圆心角为90o,半径为2,
则弧长= ,扇形面积= .π2π3.如果一个扇形面积是它所在圆的面积的 ,则此扇形的圆心角( )
(A)30° (B)36° (C)45° (D)60° 分析:C1.已知扇形的圆心角为120o,半径为6,则扇形的弧长是 ( )
A. 3π B.4π
C.5π D.6πB随堂练习2.圆心角为60°的一条弧长度是5π,则该弧的半径是( ) 153. 一个扇形的弧长为20πcm,面积是240πc㎡,则该扇形的圆心角为 .150o1.如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.3cm,求截面上有水部分的面积.(精确到0.01cm)D弓形的面积= S扇- S△C求扇形面积,需要求出∠AOB
求三角形面积,需求出OD和AB巩固提高DC∵OC=0.6,DC=0.3,∴OD=OC-DC=0.3.在Rt△OAD中,OA=0.6,利用勾股定理可得,在Rt△AOD中,∴∠OAD=30°
∴ ∠AOD=60 °,∠AOB=120°解:如图,连接OA、OB,作弦AB的垂直平分线,垂足为D,交 于点C.DC有水部分的面积∵OC=0.6 OD=0.3.
∠AOB=120°2、如图,⊙A、 ⊙B、 ⊙C、 ⊙D两两不相交,且半径都是2cm,求图中阴影部分的面积。解:因为圆的半 径相同都是2厘米,四边形的内角和为360°所以3.如图,正三角形ABC的边长为a,分别以A、B 、C 为圆心,以 为半径的圆相切于点D、E、F,求图中阴影部分的面积.ABCFED解:连接AD,则垂足为D根据勾股定理,得又知,S扇形BDF=S扇形CDE=S扇形AEF,ABCFED小 结 1. 扇形的面积大小与哪些因素有关?(1)与圆心角的大小有关(2)与半径的长短有关2. 扇形面积公式与弧长公式的区别:3.在所学的公式中,存在L、R、n、S四个量,我们只要知道其中两个就可以求得其它两个.4.扇形面积单位与弧长单位的区别:(1)扇形面积单位有平方的(2)弧长单位没有平方的
