初中数学北师大版九年级下学期 第二章 2.4 二次函数的应用(含解析)
文档属性
| 名称 | 初中数学北师大版九年级下学期 第二章 2.4 二次函数的应用(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-18 17:06:29 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
初中数学北师大版九年级下学期 第二章 2.4 二次函数的应用
一、单选题
1.如图,以40_m/s???é?????_将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2 . 下列叙述正确是( ) 【来源:21·世纪·教育·网】
A.?小球的飞行高度不能达到15m?????????????????????????????B.?小球的飞行高度可以达到25m
C.?小球从飞出到落地要用时4s????????????????????????????????D.?小球飞出1s时的飞行高度为10m
2.为了改善居民住房条件,某市计_?????¨????????¤???_的时间,将城镇居民的住房面积由现在的人均约为20平方米提高到28.8平方米,若每年的年增长率相同,设年增长率为x,则下面列出的方程中正确的是(?? )
A.??????????B.??????????C.??????????D.?
3.教练对小明推铅球的录像进行技术分析,发现某次铅球行进高度y(m)与水平距离x(m)之间的关系为y=- (x-4)2+3,由此可知小明这次的推铅球成绩是(?? ) 21cnjy.com
A.?3m??????????????????????????????????????B.?4m??????????????????????????????????????C.?8m??????????????????????????????????????D.?10m
4.若抛物线y=x2-4x-12与x轴交于点A,B,与y轴交于点C,则△ABC的面积为( ??)
A.?24?????????????????????????????????????????B.?36?????????????????????????????????????????C.?48?????????????????????????????????????????D.?96
5.如图,利用一个直_è§????è§??????????_个梯形储料场ABCD,其中∠C=120°.若新建墙BC与CD总长为12m,则该梯形储料场ABCD的最大面积是(? ) 21·cn·jy·com
A.?18m2???????????????????????????B.?m2???????????????????????????C.?m2???????????????????????????D.?m2
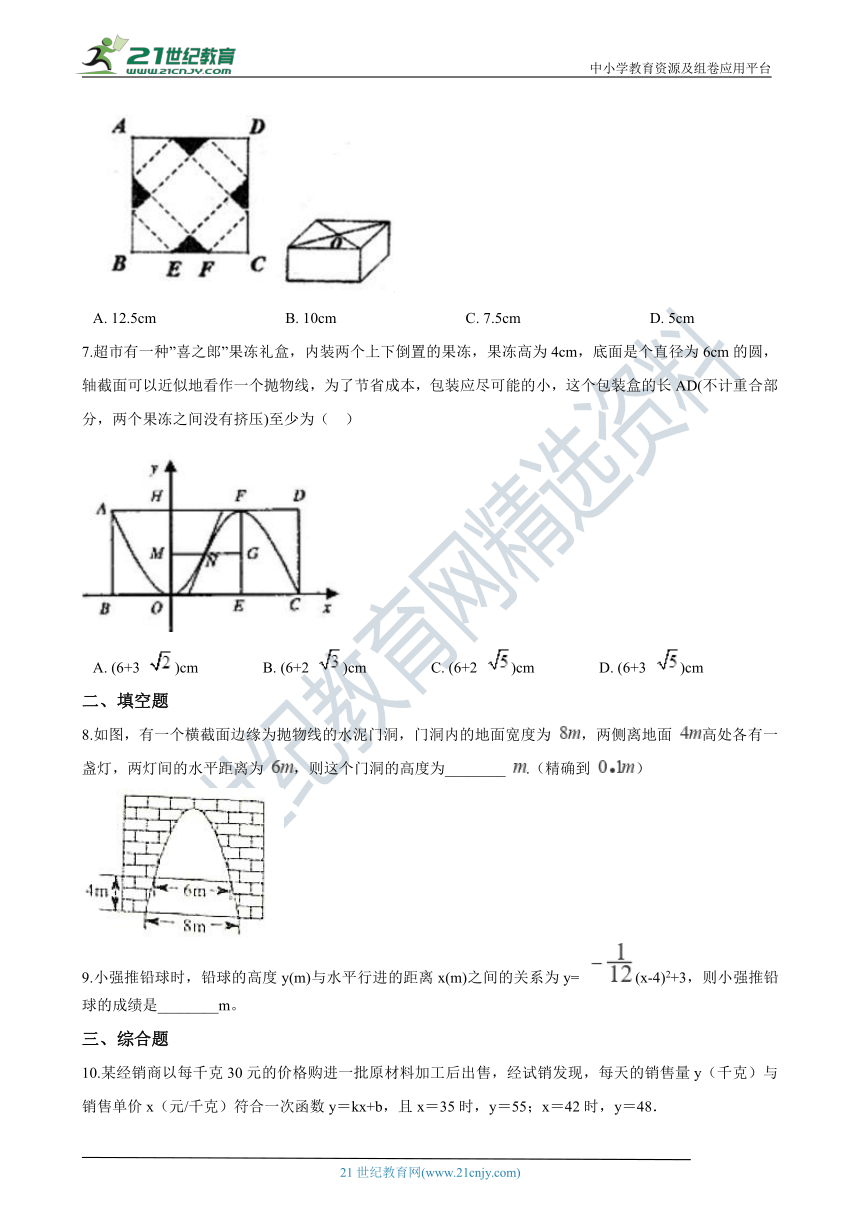
6.一种包装盒_???è??è???????????_图所示,四边形ABCD是边长为30cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四点重合于图中的点O,形成一个底面为正方形的长方体包装盒.设BE=CF=xcm,要使包装盒的侧面积最大,则x应取(??? )
A.?12.5cm??????????????????????????????????B.?10cm??????????????????????????????????C.?7.5cm??????????????????????????????????D.?5cm
7.超市有一种”喜之郎”果冻_?¤??????????è????¤_个上下倒置的果冻,果冻高为4cm,底面是个直径为6cm的圆,轴截面可以近似地看作一个抛物线,为了节省成本,包装应尽可能的小,这个包装盒的长AD(不计重合部分,两个果冻之间没有挤压)至少为( ??) www.21-cn-jy.com
A.?(6+3 )cm?????????????????B.?(6+2 )cm?????????????????C.?(6+2 )cm?????????????????D.?(6+3 )cm
二、填空题
8.如图,有一个横截面边缘为抛物线的水泥门洞,门洞内的地面宽度为 ,两侧离地面 高处各有一盏灯,两灯间的水平距离为 ,则这个门洞的高度为________ .(精确到 )
9.小强推铅球时,铅球的高度y(m)与水平行进的距离x(m)之间的关系为y= (x-4)2+3,则小强推铅球的成绩是________m。 2·1·c·n·j·y
三、综合题
10.某经销商以_?????????30???_的价格购进一批原材料加工后出售,经试销发现,每天的销售量y(千克)与销售单价x(元/千克)符合一次函数y=kx+b,且x=35时,y=55;x=42时,y=48.
(1)求一次函数y=kx+b的表达式;
(2)设该商户每天获得的销售利润为W(元),求出利润W(元)与销售单价x(元/千克)之间的关系式; www-2-1-cnjy-com
(3)销售单价每千克定为多少元时,商户每天可获得最大利润?最大利润是多少元?(销售利润=销售额﹣成本) 2-1-c-n-j-y
11.如图,已知二次函数 的图像与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
(1)求线段BC的长;
(2)当0≤y≤3时,请直接写出x的范围;
(3)点P是抛物线上位于第一象限的一个动点,连接CP,当∠BCP=90o时,求点P的坐标.
12.金秋时节,硕果飘香,某精准_???è??é???????????_上市一种有机生态水果,为帮助果园拓宽销路。欣欣超市对这种水果进行代销,进价为5元/千克,售价为6元/千克时,当天的销售量为60千克;在销售过程中发现:销售单价每上涨0.5元,当天的销售量就减少5千克.设当天销售单价统一为x元/千克(x≥6,且x按0.5元的倍数上涨),当天销售利润为y元。 21*cnjy*com
(1)求y与x的函数关系式;
(2)若该种水果每千克的利润不超过80%,求当天获得利润的范围。
13.某小区为了改善居住环境,准备修建一个巨型花园ABCD,为了节约材料并种植不同花卉,决定花园一边靠墙,三边用栅栏围住,中间用一段垂直于墙的栅栏隔成两块.已知所用栅栏的总长为60米,墙长为30米,设花园垂直于墙的一边的长为 米. 【版权所有:21教育】
(1)若平行于墙的一边长为 米,直接写出 与 的函数关系式及自变量 的取值范围;
(2)当 为何值时,这个矩形花园的面积最大?最大值为多少?(栅栏占地面积忽略不计)
(3)当这个花园的面积不小于288平方米时,试结合函数图象,直接写出 的取值范围
答案解析部分
一、单选题
1. C
A、当h=15时,15=20t﹣5t2 ,
解得:t1=1,t2=3,
故小球的飞行高度能达到15m,故此选项不符合题意;
B、h=20t﹣5t2=﹣5(t﹣2)2+20,
故t=2时,小球的飞行高度最大为:20m,故此选项不符合题意;
C、∵h=0时,0=20t﹣5t2 ,
解得:t1=0,t2=4,
∴小球从飞出到落地要用时4s,故此选项符合题意;
D、当t=1时,h=15,
故小球飞出1s时的飞行高度为15m,故此选项不符合题意;
故答案为:C.
分析:直接利用h=15以及结合配方法求出二次函数最值分别分析得出答案.
2. B
解:设每年的增长率相同,且增长率为x
∴20(1+x)2=28.8
故答案为:B.
分析:根据年平均增长率进行计算得到答案即可。
3. D
由题意得,当y=0时,
,
解得: , (舍去)
故选D.
分析:求出铅球落地时的水平距离,将y=0代入函数关系式,求出x的值即可得到成绩.
4. C
解:令y=0时,x2-4x-12=0,解,得:x1=-2,x2=6 ∴A(-2,0),B(6,0)
∴AB=6-(-2)=8
当x=0时,y=-12? ∴C(0,-12) ∴ OC=12
∴S△ABC=AB·OC=×8×12=48. 21世纪教育网版权所有
故答案为:C.
分析:先求出抛物线与x轴交于点A,B以及与y轴交于点C的坐标,进而求出△ABC的底AB和高OC,然后利用三角形的面积公式计算即可。21教育网
5. C
解:如图,过点C作CE⊥AB于E,?
则四边形ADCE为矩形,设CD=AE=x,∠DCE=∠CEB=90°,?则∠BCE=∠BCD-∠DCE=30°,BC=12-x,
在Rt△CBE中,∵∠CEB=90°,
∴梯形ABCD面积
∴当x=4时,S最大=24 .?
即CD长为4 m时,使梯形储料场ABCD的面积最大为24 ?m2。
故答案为:C。
分析:如图,过点C作CE⊥AB于E,?很容易判断出四边形ADCE为矩形,根据矩形的性质得出CD=AE=x,∠DCE=∠CEB=90°,?则∠BCE=∠BCD-∠DCE=30°,BC=12-x,在Rt△CBE中,根据含30°角的直角三角形的边之间的关系得出,根据勾股定理及矩形的性质得出, 然后根据梯形的面积计算公式即可建立出S与x的函数关系式,根据函数性质即可解决问题。
6. C
解:如图:
在Rt△GBE中,
∵BG=BE=x,
∴GE2=BG2+BE2 ,
∴GE=x,
又∵BE=CF=x,BC=30,
∴EF=30-2x,
在Rt△HEF中,
∵EH2+FH2=EF2 ,
∴EH=,
∴S侧=4××x,
=4x(30-2x),
=-8x2+120x,
=-8(x-)2+450,
∴当x=7.5时,包装盒的侧面积最大.
故答案为:C.
分析:在Rt△GBE中,根据勾股定理求得GE=x,在Rt△HEF中,根据勾股定理求得EH=, 由侧面积公式得S侧=-8(x-)2+450,根据二次函数性质即可求得答案.21·世纪*教育网
7. A
解:作NH⊥BC于点H,如图,
∴N(x,2),
设开口向上的抛物线解析式为:y=ax2 ,
∵A(-3,4)在y=ax2上,
∴9a=4,
解得:a=,
∴开口向上的抛物线解析式为:y=x2 ,
又∵N(x,2)在y=x2上,
∴2=x2 ,
解得:x=或x=-(舍去),
∴N(, 2),
∴OH=HE=,
∴AD=BC=BO+OH+HE+EC,
=3+++3,
=6+3(cm).
故答案为:A.
分析:作NH⊥BC于点H,设N(x,2),根据题意可求得开口向上的抛物线解析式为:y=x2 , 由N(x,2)在y=x2上,代入计算可得OH=HE=, 由AD=BC=BO+OH+HE+EC,计算即可得出答案.
二、填空题
8. 9.1
如图,
以地面为x轴,门洞中点为O点,画出y轴,建立直角坐标系
由题意可知各点坐标为A(-4,0)B(4,0)D(-3,4)
设抛物线解析式为y=ax2+c(a≠0)把B、D两点带入解析式
可得解析式为 ,则C(0, )
所以门洞高度为 m≈9.1m
分析:建立直角坐标系,得到二次函数,门洞高度即为二次函数的顶点的纵坐标
9. 10
令函数式 y= (x-4)2+3中,y=0,求解一元二次方程,得x1=10,x2=-2(舍去)
即铅球推出的距离是10m. 【出处:21教育名师】
分析:根据铅球落地时,高度y=0,把实际问题理解为y=0时,求x的值即可。
三、综合题
10. (1)解:将x=35、y=55和x=42、y=48代入y=kx+b,得: ,
解得: ,
∴y=﹣x+90
(2)解:根据题意_??????W??????x_﹣30)(﹣x+90)=﹣x2+120x﹣2700
(3)解:由W=﹣x2+120x﹣2700=﹣(x﹣60)2+900, 21教育名师原创作品
∴销售单价每千克定为60元时,商户每天可获得最大利润,最大利润是900元
分析:(1)运用待定系数法求解可得;(2)根据题意列出函数关系式即可;(3)结合二次函数的性质即可得函数的最值.21*cnjy*com
11. (1)解:当x=0时,y=3,∴C(0,3),∴OC=3
当y=0时 ,x1=-1,x2=4
∴A(-1,0),B(4,0),∴OA=1,OB=4
在Rt△BOC中,BC= =5
(2)解: ,
(3)解:过点P作PD⊥y轴
设点P坐标为(x, ),则点D坐标为(0, )
∴PD=x,CD= -3=
∵∠BCP=90o , ∴∠PCD+∠BCO=90°,∵∠PCD+∠CPD=90°,∴∠BCO=∠CPD
∵∠PDC=∠BOC=90o , ∴△PDC∽△COB
∴ ,∴ ,∴x= 或x=0(舍去)
当x= 时,y= ∴点P坐标为( , )
分析:(1)由y=0求出对应的x的值可得到点A,B的坐标,再由x=0求出对应的y的值,就可得到点C的坐标,然后利用点B,C的坐标,利用勾股定理就可求出BC的长。
(2)利用点A,B,C的横坐标,由0≤y≤3,就可得到对应的x的取值范围。
(3)利用函数解析式,设P坐标为(x, ) ,就可表示出点D的坐标,再用含x的代数式表示出PD,CD的长,再证明△PDC∽△COB,然后利用相似三角形的对应边成比例,建立关于x的方程,解方程求出x的值,即可得到符合题意的点P的坐标。【来源:21cnj*y.co*m】
12. (1)解:y=(x-5)(60-5× )=-10x2+170x-600
(2)解:由题意,得 ≤80%,解得x≤9,又x≥6, ∴6≤x≤9
由(1)得y=-10x2+170x-600=-10(x-8.5)2+122.5
∵对称轴为x=8.5,∴当x=8.5时,y取得最大值122.5,
当x=6时,y=60,当x=9时,y=120.
∴当天获得利润的范围为60≤y≤122.5
分析:(1)根_???????¤?é????????_润为y=每一件的利润×销售量,列出y与x的函数解析式。
(2)先将函数解析式转化为顶点式,再根据该种水果每千克的利润不超过80%,求出x的取值范围,再结合二次函数的性质分别求出x=6和x=9时的函数值,继而可求出当天获得利润的范围。
13. (1)解:如图:
∵AB+CD+EF+BC=60,AB=EF=CD=x,BC=y,
∴3x+y=60,
∴y=-3x+60(10≤x<20)
(2)解:∵S=xy=x(-3x+60),
∴S=-3x2+60x,
∵a=-3<0,
∴当x= 时,S有最大值 =300平方米
(3)解:∵这个花园的面积不小288平方米,
∴-3x2+60x≥288,
∴-3x2+60x-288≥0.
设y=-3x2+60x-288≥0.
此函数的图象如图所示:
∴当这个花园的面积不小288平方米时,出x的取值范围是:10≤x≤12.
【分_?????????1?????±_题意可知栅栏的总长60米可以看做有BC,AB,CD和EF四段组成,把已知数据代入即可求出y和x的函数关系;(2)利用矩形的面积公式:长×宽和(1)的结论即可得到S和x的关系式,再利用二次函数的性质即可求出当x为何值时,这个矩形花园的面积最大和其最大值;(3)由(2)可知函数的关系式,由此关系式画出函数的图象,结合图象可直接写出x的取值范围.
_21?????????è?????(www.21cnjy.com)_
初中数学北师大版九年级下学期 第二章 2.4 二次函数的应用
一、单选题
1.如图,以40_m/s???é?????_将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2 . 下列叙述正确是( ) 【来源:21·世纪·教育·网】
A.?小球的飞行高度不能达到15m?????????????????????????????B.?小球的飞行高度可以达到25m
C.?小球从飞出到落地要用时4s????????????????????????????????D.?小球飞出1s时的飞行高度为10m
2.为了改善居民住房条件,某市计_?????¨????????¤???_的时间,将城镇居民的住房面积由现在的人均约为20平方米提高到28.8平方米,若每年的年增长率相同,设年增长率为x,则下面列出的方程中正确的是(?? )
A.??????????B.??????????C.??????????D.?
3.教练对小明推铅球的录像进行技术分析,发现某次铅球行进高度y(m)与水平距离x(m)之间的关系为y=- (x-4)2+3,由此可知小明这次的推铅球成绩是(?? ) 21cnjy.com
A.?3m??????????????????????????????????????B.?4m??????????????????????????????????????C.?8m??????????????????????????????????????D.?10m
4.若抛物线y=x2-4x-12与x轴交于点A,B,与y轴交于点C,则△ABC的面积为( ??)
A.?24?????????????????????????????????????????B.?36?????????????????????????????????????????C.?48?????????????????????????????????????????D.?96
5.如图,利用一个直_è§????è§??????????_个梯形储料场ABCD,其中∠C=120°.若新建墙BC与CD总长为12m,则该梯形储料场ABCD的最大面积是(? ) 21·cn·jy·com
A.?18m2???????????????????????????B.?m2???????????????????????????C.?m2???????????????????????????D.?m2
6.一种包装盒_???è??è???????????_图所示,四边形ABCD是边长为30cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四点重合于图中的点O,形成一个底面为正方形的长方体包装盒.设BE=CF=xcm,要使包装盒的侧面积最大,则x应取(??? )
A.?12.5cm??????????????????????????????????B.?10cm??????????????????????????????????C.?7.5cm??????????????????????????????????D.?5cm
7.超市有一种”喜之郎”果冻_?¤??????????è????¤_个上下倒置的果冻,果冻高为4cm,底面是个直径为6cm的圆,轴截面可以近似地看作一个抛物线,为了节省成本,包装应尽可能的小,这个包装盒的长AD(不计重合部分,两个果冻之间没有挤压)至少为( ??) www.21-cn-jy.com
A.?(6+3 )cm?????????????????B.?(6+2 )cm?????????????????C.?(6+2 )cm?????????????????D.?(6+3 )cm
二、填空题
8.如图,有一个横截面边缘为抛物线的水泥门洞,门洞内的地面宽度为 ,两侧离地面 高处各有一盏灯,两灯间的水平距离为 ,则这个门洞的高度为________ .(精确到 )
9.小强推铅球时,铅球的高度y(m)与水平行进的距离x(m)之间的关系为y= (x-4)2+3,则小强推铅球的成绩是________m。 2·1·c·n·j·y
三、综合题
10.某经销商以_?????????30???_的价格购进一批原材料加工后出售,经试销发现,每天的销售量y(千克)与销售单价x(元/千克)符合一次函数y=kx+b,且x=35时,y=55;x=42时,y=48.
(1)求一次函数y=kx+b的表达式;
(2)设该商户每天获得的销售利润为W(元),求出利润W(元)与销售单价x(元/千克)之间的关系式; www-2-1-cnjy-com
(3)销售单价每千克定为多少元时,商户每天可获得最大利润?最大利润是多少元?(销售利润=销售额﹣成本) 2-1-c-n-j-y
11.如图,已知二次函数 的图像与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
(1)求线段BC的长;
(2)当0≤y≤3时,请直接写出x的范围;
(3)点P是抛物线上位于第一象限的一个动点,连接CP,当∠BCP=90o时,求点P的坐标.
12.金秋时节,硕果飘香,某精准_???è??é???????????_上市一种有机生态水果,为帮助果园拓宽销路。欣欣超市对这种水果进行代销,进价为5元/千克,售价为6元/千克时,当天的销售量为60千克;在销售过程中发现:销售单价每上涨0.5元,当天的销售量就减少5千克.设当天销售单价统一为x元/千克(x≥6,且x按0.5元的倍数上涨),当天销售利润为y元。 21*cnjy*com
(1)求y与x的函数关系式;
(2)若该种水果每千克的利润不超过80%,求当天获得利润的范围。
13.某小区为了改善居住环境,准备修建一个巨型花园ABCD,为了节约材料并种植不同花卉,决定花园一边靠墙,三边用栅栏围住,中间用一段垂直于墙的栅栏隔成两块.已知所用栅栏的总长为60米,墙长为30米,设花园垂直于墙的一边的长为 米. 【版权所有:21教育】
(1)若平行于墙的一边长为 米,直接写出 与 的函数关系式及自变量 的取值范围;
(2)当 为何值时,这个矩形花园的面积最大?最大值为多少?(栅栏占地面积忽略不计)
(3)当这个花园的面积不小于288平方米时,试结合函数图象,直接写出 的取值范围
答案解析部分
一、单选题
1. C
A、当h=15时,15=20t﹣5t2 ,
解得:t1=1,t2=3,
故小球的飞行高度能达到15m,故此选项不符合题意;
B、h=20t﹣5t2=﹣5(t﹣2)2+20,
故t=2时,小球的飞行高度最大为:20m,故此选项不符合题意;
C、∵h=0时,0=20t﹣5t2 ,
解得:t1=0,t2=4,
∴小球从飞出到落地要用时4s,故此选项符合题意;
D、当t=1时,h=15,
故小球飞出1s时的飞行高度为15m,故此选项不符合题意;
故答案为:C.
分析:直接利用h=15以及结合配方法求出二次函数最值分别分析得出答案.
2. B
解:设每年的增长率相同,且增长率为x
∴20(1+x)2=28.8
故答案为:B.
分析:根据年平均增长率进行计算得到答案即可。
3. D
由题意得,当y=0时,
,
解得: , (舍去)
故选D.
分析:求出铅球落地时的水平距离,将y=0代入函数关系式,求出x的值即可得到成绩.
4. C
解:令y=0时,x2-4x-12=0,解,得:x1=-2,x2=6 ∴A(-2,0),B(6,0)
∴AB=6-(-2)=8
当x=0时,y=-12? ∴C(0,-12) ∴ OC=12
∴S△ABC=AB·OC=×8×12=48. 21世纪教育网版权所有
故答案为:C.
分析:先求出抛物线与x轴交于点A,B以及与y轴交于点C的坐标,进而求出△ABC的底AB和高OC,然后利用三角形的面积公式计算即可。21教育网
5. C
解:如图,过点C作CE⊥AB于E,?
则四边形ADCE为矩形,设CD=AE=x,∠DCE=∠CEB=90°,?则∠BCE=∠BCD-∠DCE=30°,BC=12-x,
在Rt△CBE中,∵∠CEB=90°,
∴梯形ABCD面积
∴当x=4时,S最大=24 .?
即CD长为4 m时,使梯形储料场ABCD的面积最大为24 ?m2。
故答案为:C。
分析:如图,过点C作CE⊥AB于E,?很容易判断出四边形ADCE为矩形,根据矩形的性质得出CD=AE=x,∠DCE=∠CEB=90°,?则∠BCE=∠BCD-∠DCE=30°,BC=12-x,在Rt△CBE中,根据含30°角的直角三角形的边之间的关系得出,根据勾股定理及矩形的性质得出, 然后根据梯形的面积计算公式即可建立出S与x的函数关系式,根据函数性质即可解决问题。
6. C
解:如图:
在Rt△GBE中,
∵BG=BE=x,
∴GE2=BG2+BE2 ,
∴GE=x,
又∵BE=CF=x,BC=30,
∴EF=30-2x,
在Rt△HEF中,
∵EH2+FH2=EF2 ,
∴EH=,
∴S侧=4××x,
=4x(30-2x),
=-8x2+120x,
=-8(x-)2+450,
∴当x=7.5时,包装盒的侧面积最大.
故答案为:C.
分析:在Rt△GBE中,根据勾股定理求得GE=x,在Rt△HEF中,根据勾股定理求得EH=, 由侧面积公式得S侧=-8(x-)2+450,根据二次函数性质即可求得答案.21·世纪*教育网
7. A
解:作NH⊥BC于点H,如图,
∴N(x,2),
设开口向上的抛物线解析式为:y=ax2 ,
∵A(-3,4)在y=ax2上,
∴9a=4,
解得:a=,
∴开口向上的抛物线解析式为:y=x2 ,
又∵N(x,2)在y=x2上,
∴2=x2 ,
解得:x=或x=-(舍去),
∴N(, 2),
∴OH=HE=,
∴AD=BC=BO+OH+HE+EC,
=3+++3,
=6+3(cm).
故答案为:A.
分析:作NH⊥BC于点H,设N(x,2),根据题意可求得开口向上的抛物线解析式为:y=x2 , 由N(x,2)在y=x2上,代入计算可得OH=HE=, 由AD=BC=BO+OH+HE+EC,计算即可得出答案.
二、填空题
8. 9.1
如图,
以地面为x轴,门洞中点为O点,画出y轴,建立直角坐标系
由题意可知各点坐标为A(-4,0)B(4,0)D(-3,4)
设抛物线解析式为y=ax2+c(a≠0)把B、D两点带入解析式
可得解析式为 ,则C(0, )
所以门洞高度为 m≈9.1m
分析:建立直角坐标系,得到二次函数,门洞高度即为二次函数的顶点的纵坐标
9. 10
令函数式 y= (x-4)2+3中,y=0,求解一元二次方程,得x1=10,x2=-2(舍去)
即铅球推出的距离是10m. 【出处:21教育名师】
分析:根据铅球落地时,高度y=0,把实际问题理解为y=0时,求x的值即可。
三、综合题
10. (1)解:将x=35、y=55和x=42、y=48代入y=kx+b,得: ,
解得: ,
∴y=﹣x+90
(2)解:根据题意_??????W??????x_﹣30)(﹣x+90)=﹣x2+120x﹣2700
(3)解:由W=﹣x2+120x﹣2700=﹣(x﹣60)2+900, 21教育名师原创作品
∴销售单价每千克定为60元时,商户每天可获得最大利润,最大利润是900元
分析:(1)运用待定系数法求解可得;(2)根据题意列出函数关系式即可;(3)结合二次函数的性质即可得函数的最值.21*cnjy*com
11. (1)解:当x=0时,y=3,∴C(0,3),∴OC=3
当y=0时 ,x1=-1,x2=4
∴A(-1,0),B(4,0),∴OA=1,OB=4
在Rt△BOC中,BC= =5
(2)解: ,
(3)解:过点P作PD⊥y轴
设点P坐标为(x, ),则点D坐标为(0, )
∴PD=x,CD= -3=
∵∠BCP=90o , ∴∠PCD+∠BCO=90°,∵∠PCD+∠CPD=90°,∴∠BCO=∠CPD
∵∠PDC=∠BOC=90o , ∴△PDC∽△COB
∴ ,∴ ,∴x= 或x=0(舍去)
当x= 时,y= ∴点P坐标为( , )
分析:(1)由y=0求出对应的x的值可得到点A,B的坐标,再由x=0求出对应的y的值,就可得到点C的坐标,然后利用点B,C的坐标,利用勾股定理就可求出BC的长。
(2)利用点A,B,C的横坐标,由0≤y≤3,就可得到对应的x的取值范围。
(3)利用函数解析式,设P坐标为(x, ) ,就可表示出点D的坐标,再用含x的代数式表示出PD,CD的长,再证明△PDC∽△COB,然后利用相似三角形的对应边成比例,建立关于x的方程,解方程求出x的值,即可得到符合题意的点P的坐标。【来源:21cnj*y.co*m】
12. (1)解:y=(x-5)(60-5× )=-10x2+170x-600
(2)解:由题意,得 ≤80%,解得x≤9,又x≥6, ∴6≤x≤9
由(1)得y=-10x2+170x-600=-10(x-8.5)2+122.5
∵对称轴为x=8.5,∴当x=8.5时,y取得最大值122.5,
当x=6时,y=60,当x=9时,y=120.
∴当天获得利润的范围为60≤y≤122.5
分析:(1)根_???????¤?é????????_润为y=每一件的利润×销售量,列出y与x的函数解析式。
(2)先将函数解析式转化为顶点式,再根据该种水果每千克的利润不超过80%,求出x的取值范围,再结合二次函数的性质分别求出x=6和x=9时的函数值,继而可求出当天获得利润的范围。
13. (1)解:如图:
∵AB+CD+EF+BC=60,AB=EF=CD=x,BC=y,
∴3x+y=60,
∴y=-3x+60(10≤x<20)
(2)解:∵S=xy=x(-3x+60),
∴S=-3x2+60x,
∵a=-3<0,
∴当x= 时,S有最大值 =300平方米
(3)解:∵这个花园的面积不小288平方米,
∴-3x2+60x≥288,
∴-3x2+60x-288≥0.
设y=-3x2+60x-288≥0.
此函数的图象如图所示:
∴当这个花园的面积不小288平方米时,出x的取值范围是:10≤x≤12.
【分_?????????1?????±_题意可知栅栏的总长60米可以看做有BC,AB,CD和EF四段组成,把已知数据代入即可求出y和x的函数关系;(2)利用矩形的面积公式:长×宽和(1)的结论即可得到S和x的关系式,再利用二次函数的性质即可求出当x为何值时,这个矩形花园的面积最大和其最大值;(3)由(2)可知函数的关系式,由此关系式画出函数的图象,结合图象可直接写出x的取值范围.
_21?????????è?????(www.21cnjy.com)_
