初中数学北师大版九年级下学期 第二章 2.5 二次函数与一元二次方程(含解析)
文档属性
| 名称 | 初中数学北师大版九年级下学期 第二章 2.5 二次函数与一元二次方程(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-18 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
初中数学北师大版九年级下学期 第二章 2.5 二次函数与一元二次方程
一、单选题
1.抛物线y=x2+2x+3与y轴的交点为(??? )
A.?(0,2)?????????????????????????????????B.?(2,0)?????????????????????????????????C.?(0,3)?????????????????????????????????D.?(3,0)
2.已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)的对应值如下表所示:
x … 0 4 …
y … 0.37 -1 0.37 …
则方程ax2+bx+1.37=0的根是( ???)
A.?0或4???????????????????????????????B.?或4- ???????????????????????????????C.?1或5???????????????????????????????D.?无实根
3.已知函数y=(k-1)x2-4x+4与x轴只有一个交点,则k的取值范围是(??? )
A.?且 ???????????????????????B.?且 ???????????????????????C.?????????????????????????D.?或1
4.已知函数 ,并且 , 是方程 的两个根,则实数 , , , 的大小关系可能是(??? ) 21世纪教育网版权所有
A.??????????????????B.??????????????????C.??????????????????D.?
5.已知函数 ,其几对对应值如表,判断方程 为常数)的根的个数( )
6.17 6.18 6.19 6.20
0.02 -0.01 0.02 0.04
A.?0??????????????????????????????????????????B.?1??????????????????????????????????????????C.?2??????????????????????????????????????????D.?1或2
6.若关于x的方程x2﹣mx+n=0没有实数解,则抛物线y=x2﹣mx+n与x轴的交点有(?? )
A.?2个????????????????????????????????????B.?1个????????????????????????????????????C.?0个????????????????????????????????????D.?不能确定
二、填空题
7.抛物线y=x2-9与y轴的交点坐标为________。
8.如图,二次函数_y=ax2+_bx+c的图象与x轴交于(﹣2,0)和(4,0)两点,当函数值y>0时,自变量x的取值范围是________ 21教育网
9.抛物线 与 轴有________个交点.
10.已知关于x的方_?¨?2+???x???_m)(x﹣n)=0,存在a,b是方程2+(x﹣m)(x﹣n)=0的两个根,则实数m,n,a,b的大小关系可能是________. www.21-cn-jy.com
11.对于二次函数 的描述,下列命题:①若 ,则b2-4ac≥0;②若 ,则一元二次方程 有两个不相等的实数根;③若 ,则二次函数 的图象与坐标轴的公共点的个数是2或3;④若 ,则一元二次方程 有两个不相等的实数根.其中结论正确的有________(填写所有正确的序号).
12.如图是_???????????°y???_﹣x2+4x的图象,若关于x的一元二次方程﹣x2+4x﹣t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是________. 2·1·c·n·j·y
13.二次函数y=﹣2x2﹣3x+k的图象在x轴下方,则k的取值范围是________.
答案解析部分
一、单选题
1. C
解:当x=0时,y=3
∴抛物线与y轴的交点坐标为(0,3)
故答案为:C
分析:要求抛物线与y轴的交点坐标,由x=0求出对应的y的值,即可得到答案。
2. B
解:由列表可知,当x=0时, y= c=0.37,
∴y= ax2+bx+0.37=0 ,
由ax2+bx+1.37=0?,得ax2+bx+0.37=-1?,
∵由列表可得当x=, ax2+bx+0.37=-1?,
∴x=是 ax2+bx+1.37=0的根 ,
∵?当x=0或x=4时y=ax2+bx+c=0,
∴抛物线的对称轴为x=
∴y=ax2+bx+1.37的对称轴和 y=ax2+bx+c一致??,
∴
解得x2=4-.
故答案为:B.
分析:先由x=0, 求得C值,从列表中得出当x=, ax2+bx+0.37=-1?,由此推出∴x=是 ax2+bx+1.37=0的一个根 ,因为二次函数图象是对称图形,且y=ax2+bx+1.37的对称轴和 y=ax2+bx+c一致??,于是求得对称轴方程为x=2, 再结合一根为, 代入对称轴方程即可求出另一个根.
3. D
解:当k-1=0,即k=1时,函数为y=-4x+4,与x轴只有一个交点;
当k-1≠0,即k≠1时,令y=0可得(k-1)x2-4x+4=0,由函数与x轴只有一个交点可知该方程有两个相等的实数根,【来源:21·世纪·教育·网】
∴△=0,即(-4)2-4(k-1)×4=0,解得k=2,
综上可知k的值为1或2,
故答案为:D .
分析:本题主要考查函数_???xè???????¤???_,掌握二次函数与x轴只有一个交点的条件是解题的关键,注意分类讨论.当k+1=0时,函数为一次函数必与x轴有一个交点;当k+1≠0时,令y=0可得到关于x的一元二次方程,根据条件可知其判别式为0,可求得k的值.21·世纪*教育网
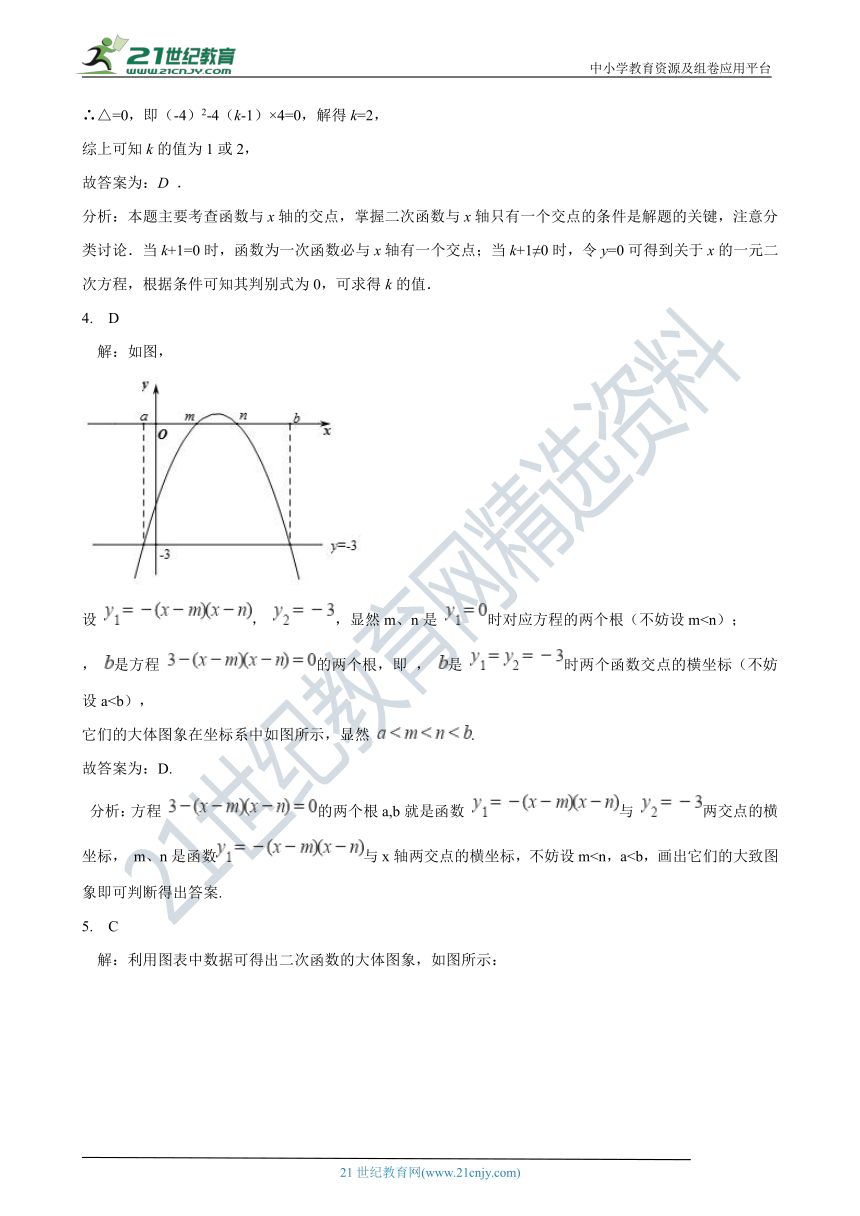
4. D
解:如图,
设 , ,显然m、n是 时对应方程的两个根(不妨设m, 是方程 的两个根,即 , 是 时两个函数交点的横坐标(不妨设a它们的大体图象在坐标系中如图所示,显然 .
故答案为:D.
分析:方程 的两个根a,b就是函数 与 两交点的横坐标, m、n是函数与x轴两交点的横坐标,不妨设m5. C
解:利用图表中数据可得出二次函数的大体图象,如图所示:
即图象与x轴交点个数为2个,即方程ax2+bx+c=0的根的个数是2.
故答案为:C.
分析:利用表格中数据得出二次函数图象的大体位置,再结合一元二次方程的性质得出即可.
6. C
解:x2﹣mx+n=0没有实数解,则抛物线y=x2﹣mx+n与x轴没有交点,
故答案为:C.
分析:根据二次函数与x轴相交_???y=0??????_得关于x的一元二次方程,再根据一元二次方程的根的判别式“①当b2-4ac>0时,方程有两个不相等的实数根;②当b2-4ac=0时,方程有两个相等的实数根;③当b2-4ac<0时,方程没有实数根。”即可判断求解.21*cnjy*com
二、填空题
7. (0,-9)
解:当x=0时,y=-9
∴此抛物线与y轴的交点坐标为(0,-9).
故答案为:(0,-9).【来源:21cnj*y.co*m】
分析:要求二次函数图像与y轴的交点坐标,利用函数解析式,由x=0求出对应的函数y的值,即可得到抛物线与y轴的交点坐标。【出处:21教育名师】
8. -2 解:看图_è±?????????????__-20,
故答案为: -2
分析: 函数值y>0时,?只要找出图象在x轴上方时自变量x的范围即可.21cnjy.com
9. 2
解:令y=0,得 ,
则
方程有两个不相等的实数根,
所以抛物线 与 轴有2个交点.
故答案为:2
分析:令y=0,得到一元二次方程,求其判别式,根据一元二次方程与二次函数的关系可得解.
10. m<a<b<n
解:令函数y=2+(x﹣m)(x﹣n)=x2﹣(m+n)x+mn+2,
∴抛物线开口向上,
令y=0,根据题意得到方程(x﹣m)(x﹣n)=﹣2的两个根为a,b,
∵当x=m或n时,y=2>0,
∴实数m,n,a,b的大小关系为m<a<b<n.
分析:令抛物线解析式中y=_0????????°????¨?_的解为a,b,即为抛物线与x轴交点的横坐标为a,b,再由抛物线开口向上得到a<x<b时y小于0,得到x=m与n时函数值大于0,即可确定出m,n,a,b的大小关系.21·cn·jy·com
11. ①②③
解:①若 ,则 ,
∴ ,故正确;②若 ,则 ,
∵a≠0,
∴ 与 不会同时为0,
∴ ,故正确;③∵ ,
∴二次函数 的图象与x轴有两个交点,而二次函数 与y轴必有一个交点,这个交点有可能跟图象与x轴的交点重合,2-1-c-n-j-y
∴二次函数 的图象与坐标轴的公共点的个数是2或3,故正确;④∵根据 无法判断△的大小,
∴不能得出一元二次方程 有两个不相等的实数根,故错误,
∴其中结论正确的有①②③,
故答案为:①②③.
分析:①②可通过变形得到 与0的大小关系,从而进行判断;③可根据 得到二次函数图象与x轴有两个交点,但是不能忽略与y轴的交点可能跟图象与x轴的交点重合,从而进而判断;而④无法得到 与0的大小关系,故错误.【版权所有:21教育】
12. ﹣5<t≤4
求-x2+4x_???t=0??????_求-x2+4x=t在1分析:求-x2+4x-t=0在113. k<﹣
因为二次函数y=﹣2x2﹣3x+k的图象在x轴下方,所以△<0,即(﹣3)2﹣4×(﹣2)k<0,解得k<﹣ ,故答案为k<﹣ .
分析:由于二次函数y=﹣2x2﹣3x+k的二次项系数为-2,所以图像开口向下,同时图象在x轴下方,所以图像与x轴无交点,即△<0,解得k<﹣ 。21*cnjy*com
_21?????????è?????(www.21cnjy.com)_
初中数学北师大版九年级下学期 第二章 2.5 二次函数与一元二次方程
一、单选题
1.抛物线y=x2+2x+3与y轴的交点为(??? )
A.?(0,2)?????????????????????????????????B.?(2,0)?????????????????????????????????C.?(0,3)?????????????????????????????????D.?(3,0)
2.已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)的对应值如下表所示:
x … 0 4 …
y … 0.37 -1 0.37 …
则方程ax2+bx+1.37=0的根是( ???)
A.?0或4???????????????????????????????B.?或4- ???????????????????????????????C.?1或5???????????????????????????????D.?无实根
3.已知函数y=(k-1)x2-4x+4与x轴只有一个交点,则k的取值范围是(??? )
A.?且 ???????????????????????B.?且 ???????????????????????C.?????????????????????????D.?或1
4.已知函数 ,并且 , 是方程 的两个根,则实数 , , , 的大小关系可能是(??? ) 21世纪教育网版权所有
A.??????????????????B.??????????????????C.??????????????????D.?
5.已知函数 ,其几对对应值如表,判断方程 为常数)的根的个数( )
6.17 6.18 6.19 6.20
0.02 -0.01 0.02 0.04
A.?0??????????????????????????????????????????B.?1??????????????????????????????????????????C.?2??????????????????????????????????????????D.?1或2
6.若关于x的方程x2﹣mx+n=0没有实数解,则抛物线y=x2﹣mx+n与x轴的交点有(?? )
A.?2个????????????????????????????????????B.?1个????????????????????????????????????C.?0个????????????????????????????????????D.?不能确定
二、填空题
7.抛物线y=x2-9与y轴的交点坐标为________。
8.如图,二次函数_y=ax2+_bx+c的图象与x轴交于(﹣2,0)和(4,0)两点,当函数值y>0时,自变量x的取值范围是________ 21教育网
9.抛物线 与 轴有________个交点.
10.已知关于x的方_?¨?2+???x???_m)(x﹣n)=0,存在a,b是方程2+(x﹣m)(x﹣n)=0的两个根,则实数m,n,a,b的大小关系可能是________. www.21-cn-jy.com
11.对于二次函数 的描述,下列命题:①若 ,则b2-4ac≥0;②若 ,则一元二次方程 有两个不相等的实数根;③若 ,则二次函数 的图象与坐标轴的公共点的个数是2或3;④若 ,则一元二次方程 有两个不相等的实数根.其中结论正确的有________(填写所有正确的序号).
12.如图是_???????????°y???_﹣x2+4x的图象,若关于x的一元二次方程﹣x2+4x﹣t=0(t为实数)在1<x<5的范围内有解,则t的取值范围是________. 2·1·c·n·j·y
13.二次函数y=﹣2x2﹣3x+k的图象在x轴下方,则k的取值范围是________.
答案解析部分
一、单选题
1. C
解:当x=0时,y=3
∴抛物线与y轴的交点坐标为(0,3)
故答案为:C
分析:要求抛物线与y轴的交点坐标,由x=0求出对应的y的值,即可得到答案。
2. B
解:由列表可知,当x=0时, y= c=0.37,
∴y= ax2+bx+0.37=0 ,
由ax2+bx+1.37=0?,得ax2+bx+0.37=-1?,
∵由列表可得当x=, ax2+bx+0.37=-1?,
∴x=是 ax2+bx+1.37=0的根 ,
∵?当x=0或x=4时y=ax2+bx+c=0,
∴抛物线的对称轴为x=
∴y=ax2+bx+1.37的对称轴和 y=ax2+bx+c一致??,
∴
解得x2=4-.
故答案为:B.
分析:先由x=0, 求得C值,从列表中得出当x=, ax2+bx+0.37=-1?,由此推出∴x=是 ax2+bx+1.37=0的一个根 ,因为二次函数图象是对称图形,且y=ax2+bx+1.37的对称轴和 y=ax2+bx+c一致??,于是求得对称轴方程为x=2, 再结合一根为, 代入对称轴方程即可求出另一个根.
3. D
解:当k-1=0,即k=1时,函数为y=-4x+4,与x轴只有一个交点;
当k-1≠0,即k≠1时,令y=0可得(k-1)x2-4x+4=0,由函数与x轴只有一个交点可知该方程有两个相等的实数根,【来源:21·世纪·教育·网】
∴△=0,即(-4)2-4(k-1)×4=0,解得k=2,
综上可知k的值为1或2,
故答案为:D .
分析:本题主要考查函数_???xè???????¤???_,掌握二次函数与x轴只有一个交点的条件是解题的关键,注意分类讨论.当k+1=0时,函数为一次函数必与x轴有一个交点;当k+1≠0时,令y=0可得到关于x的一元二次方程,根据条件可知其判别式为0,可求得k的值.21·世纪*教育网
4. D
解:如图,
设 , ,显然m、n是 时对应方程的两个根(不妨设m
故答案为:D.
分析:方程 的两个根a,b就是函数 与 两交点的横坐标, m、n是函数与x轴两交点的横坐标,不妨设m
解:利用图表中数据可得出二次函数的大体图象,如图所示:
即图象与x轴交点个数为2个,即方程ax2+bx+c=0的根的个数是2.
故答案为:C.
分析:利用表格中数据得出二次函数图象的大体位置,再结合一元二次方程的性质得出即可.
6. C
解:x2﹣mx+n=0没有实数解,则抛物线y=x2﹣mx+n与x轴没有交点,
故答案为:C.
分析:根据二次函数与x轴相交_???y=0??????_得关于x的一元二次方程,再根据一元二次方程的根的判别式“①当b2-4ac>0时,方程有两个不相等的实数根;②当b2-4ac=0时,方程有两个相等的实数根;③当b2-4ac<0时,方程没有实数根。”即可判断求解.21*cnjy*com
二、填空题
7. (0,-9)
解:当x=0时,y=-9
∴此抛物线与y轴的交点坐标为(0,-9).
故答案为:(0,-9).【来源:21cnj*y.co*m】
分析:要求二次函数图像与y轴的交点坐标,利用函数解析式,由x=0求出对应的函数y的值,即可得到抛物线与y轴的交点坐标。【出处:21教育名师】
8. -2
故答案为: -2
分析: 函数值y>0时,?只要找出图象在x轴上方时自变量x的范围即可.21cnjy.com
9. 2
解:令y=0,得 ,
则
方程有两个不相等的实数根,
所以抛物线 与 轴有2个交点.
故答案为:2
分析:令y=0,得到一元二次方程,求其判别式,根据一元二次方程与二次函数的关系可得解.
10. m<a<b<n
解:令函数y=2+(x﹣m)(x﹣n)=x2﹣(m+n)x+mn+2,
∴抛物线开口向上,
令y=0,根据题意得到方程(x﹣m)(x﹣n)=﹣2的两个根为a,b,
∵当x=m或n时,y=2>0,
∴实数m,n,a,b的大小关系为m<a<b<n.
分析:令抛物线解析式中y=_0????????°????¨?_的解为a,b,即为抛物线与x轴交点的横坐标为a,b,再由抛物线开口向上得到a<x<b时y小于0,得到x=m与n时函数值大于0,即可确定出m,n,a,b的大小关系.21·cn·jy·com
11. ①②③
解:①若 ,则 ,
∴ ,故正确;②若 ,则 ,
∵a≠0,
∴ 与 不会同时为0,
∴ ,故正确;③∵ ,
∴二次函数 的图象与x轴有两个交点,而二次函数 与y轴必有一个交点,这个交点有可能跟图象与x轴的交点重合,2-1-c-n-j-y
∴二次函数 的图象与坐标轴的公共点的个数是2或3,故正确;④∵根据 无法判断△的大小,
∴不能得出一元二次方程 有两个不相等的实数根,故错误,
∴其中结论正确的有①②③,
故答案为:①②③.
分析:①②可通过变形得到 与0的大小关系,从而进行判断;③可根据 得到二次函数图象与x轴有两个交点,但是不能忽略与y轴的交点可能跟图象与x轴的交点重合,从而进而判断;而④无法得到 与0的大小关系,故错误.【版权所有:21教育】
12. ﹣5<t≤4
求-x2+4x_???t=0??????_求-x2+4x=t在1
因为二次函数y=﹣2x2﹣3x+k的图象在x轴下方,所以△<0,即(﹣3)2﹣4×(﹣2)k<0,解得k<﹣ ,故答案为k<﹣ .
分析:由于二次函数y=﹣2x2﹣3x+k的二次项系数为-2,所以图像开口向下,同时图象在x轴下方,所以图像与x轴无交点,即△<0,解得k<﹣ 。21*cnjy*com
_21?????????è?????(www.21cnjy.com)_
