初中数学北师大版九年级下学期 第三章 3.2 圆的对称性(含解析)
文档属性
| 名称 | 初中数学北师大版九年级下学期 第三章 3.2 圆的对称性(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-18 17:16:13 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
初中数学北师大版九年级下学期 第三章 3.2 圆的对称性
一、单选题
1.如图,AB是⊙O的直径, ,∠COD=34°,则∠AOE的度数是(??? )
A.?51°???????????????????????????????????????B.?56°???????????????????????????????????????C.?68°???????????????????????????????????????D.?78°
2.如图,在⊙O中,若点C是 的中点,∠A=50°,则∠BOC=( ???)
A.?40°???????????????????????????????????????B.?45°???????????????????????????????????????C.?50°???????????????????????????????????????D.?60°
3.如下图,已知AB是⊙O的直径, = = ,∠BOC=40°,那么∠AOE等于(?? )
A.?40°??????????????????????????????????????B.?50°??????????????????????????????????????C.?60°??????????????????????????????????????D.?120°
4.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=10,AE=2,则弦CD的长是(?? )
A.?4???????????????????????????????????????????B.?6???????????????????????????????????????????C.?8???????????????????????????????????????????D.?10
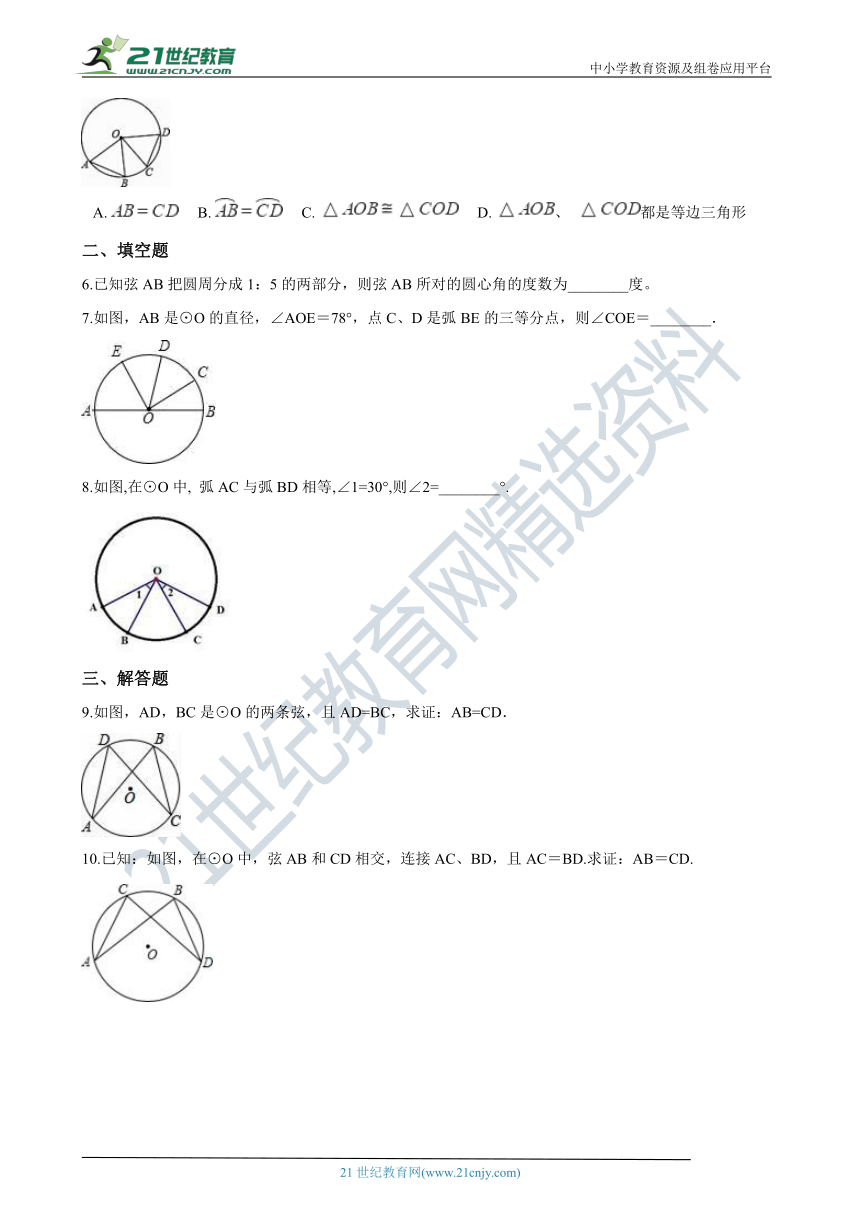
5.已知,如图, ,下列结论不一定成立的是( ??)
A.??????B.??????C.??????D.?、 都是等边三角形
二、填空题
6.已知弦AB把圆周分成1:5的两部分,则弦AB所对的圆心角的度数为________度。
7.如图,AB是⊙O的直径,∠AOE=78°,点C、D是弧BE的三等分点,则∠COE=________.
8.如图,在⊙O中, 弧AC与弧BD相等,∠1=30°,则∠2=________°.
三、解答题
9.如图,AD,BC是⊙O的两条弦,且AD=BC,求证:AB=CD.
10.已知:如图,在⊙O中,弦AB和CD相交,连接AC、BD,且AC=BD.求证:AB=CD.
答案解析部分
一、单选题
1. D
解:∵ , ∠COD=34° ,
∴∠BOC=∠COD=∠DOE=34°,
∴∠AOE=180°-∠BOC-∠COD-∠DOE=180°-34°-34°-34°= 78° .
故答案为:D.
分析:根据等弧所对的圆心角相等得出∠BOC=∠COD=∠DOE=34°,进而根据角的和差就可算出答案.
2. A
∵OA=OB,∴∠B=∠A=50°,∠AOB=80°,
又∵C是 的中点 ,
∴∠BOC=∠AOC=40°。
故答案为:A。
分析:由OA=OB,可求得∠AOB的大小,由 C是 的中点可得出弧AC等于弧BC,故∠BOC=∠AOC=40°。21教育网
3. C
∵ ,∠BOC=40°
∴∠BOE=3∠BOC=120°
∴∠AOE=180-∠BOE=60°
故答案为:C.
分析:根据圆心角与弦的关系可求得∠BOE的度数,从而即可求解.
4. C
解:连接OC,
∵AB为⊙O的直径,AB⊥CD,
∴CE=DE= CD,
在Rt△OCE中,OC2=OE2+CE2 ,
∵AE=2,AB=10,
∴OC=5,OE=3,
∴CE=4,
∴CD=8,
故答案为:C.
分析:连接OC,利用直径垂直平分弦以及勾股定理解出CD的长度。
5. D
∵∠AOB=∠_COD???
???_AB=CD,OA=OB=OC=OD,
∴△AOB≌△COD,
∴A、B、C成立,则D不成立,
故答案为:D21cnjy.com
分析:利用圆心角、弧、弦的关系定理,可证得AB=CD,弧AB=CD,再利用SSS可证得△AOB≌△COD,即可得出不一定成立的结论。21·cn·jy·com
二、填空题
6. 60
解:?∵弦AB把圆周分成1:5的两部分,
AB所对的圆心角度数为:
故答案为:60.
分析:由于弦AB把圆周分成1:5的两部分, 根据圆心角、弧、弦的关系得到弦AB所对的圆心角为圆周的.www.21-cn-jy.com
7. 68°
∵∠AOE=78°,∴劣弧 的度数为78°.
∵AB是⊙O的直径,∴劣弧 的度数为180°﹣78°=102°.
∵点C、D是弧BE的三等分点,∴∠COE 102°=68°.
故答案为:68°.
分析:根据∠AOE的度数求出劣弧 的度数,得到劣弧 的度数,根据圆心角、弧、弦的关系定理解答即可.2·1·c·n·j·y
8. 30
_è§???????_??§A_C与弧BD相等,
∴弧AB和弧CD相等,
∴∠2=∠1=30° ;
故答案为:30.
分析:由弧AC与弧BD相等推得弧AB和弧CD相等,再根据在同圆中,等弧所对的圆周角相等,从而求出∠2的度数.【来源:21·世纪·教育·网】
三、解答题
9. 证明:∵AD=BC,
∴ .
∴ .
∴ .
∴AB=CD
分析: 根据同圆中,相等的弦所对的弧相等得出?? , 进而根据等式的性质得出?, 最后根据等弧所对的弦相等即可得出AB=CD.21世纪教育网版权所有
10. 证明:∵AC=BD,
∴ .
∴
∴ .
∴AB=CD
分析:根据同圆中相等的弦所对的弧相等得出 ,根据等式的性质得出 ,根据同圆中相等的弧所对的弦相等得出AB=CD.21·世纪*教育网
_21?????????è?????(www.21cnjy.com)_
初中数学北师大版九年级下学期 第三章 3.2 圆的对称性
一、单选题
1.如图,AB是⊙O的直径, ,∠COD=34°,则∠AOE的度数是(??? )
A.?51°???????????????????????????????????????B.?56°???????????????????????????????????????C.?68°???????????????????????????????????????D.?78°
2.如图,在⊙O中,若点C是 的中点,∠A=50°,则∠BOC=( ???)
A.?40°???????????????????????????????????????B.?45°???????????????????????????????????????C.?50°???????????????????????????????????????D.?60°
3.如下图,已知AB是⊙O的直径, = = ,∠BOC=40°,那么∠AOE等于(?? )
A.?40°??????????????????????????????????????B.?50°??????????????????????????????????????C.?60°??????????????????????????????????????D.?120°
4.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=10,AE=2,则弦CD的长是(?? )
A.?4???????????????????????????????????????????B.?6???????????????????????????????????????????C.?8???????????????????????????????????????????D.?10
5.已知,如图, ,下列结论不一定成立的是( ??)
A.??????B.??????C.??????D.?、 都是等边三角形
二、填空题
6.已知弦AB把圆周分成1:5的两部分,则弦AB所对的圆心角的度数为________度。
7.如图,AB是⊙O的直径,∠AOE=78°,点C、D是弧BE的三等分点,则∠COE=________.
8.如图,在⊙O中, 弧AC与弧BD相等,∠1=30°,则∠2=________°.
三、解答题
9.如图,AD,BC是⊙O的两条弦,且AD=BC,求证:AB=CD.
10.已知:如图,在⊙O中,弦AB和CD相交,连接AC、BD,且AC=BD.求证:AB=CD.
答案解析部分
一、单选题
1. D
解:∵ , ∠COD=34° ,
∴∠BOC=∠COD=∠DOE=34°,
∴∠AOE=180°-∠BOC-∠COD-∠DOE=180°-34°-34°-34°= 78° .
故答案为:D.
分析:根据等弧所对的圆心角相等得出∠BOC=∠COD=∠DOE=34°,进而根据角的和差就可算出答案.
2. A
∵OA=OB,∴∠B=∠A=50°,∠AOB=80°,
又∵C是 的中点 ,
∴∠BOC=∠AOC=40°。
故答案为:A。
分析:由OA=OB,可求得∠AOB的大小,由 C是 的中点可得出弧AC等于弧BC,故∠BOC=∠AOC=40°。21教育网
3. C
∵ ,∠BOC=40°
∴∠BOE=3∠BOC=120°
∴∠AOE=180-∠BOE=60°
故答案为:C.
分析:根据圆心角与弦的关系可求得∠BOE的度数,从而即可求解.
4. C
解:连接OC,
∵AB为⊙O的直径,AB⊥CD,
∴CE=DE= CD,
在Rt△OCE中,OC2=OE2+CE2 ,
∵AE=2,AB=10,
∴OC=5,OE=3,
∴CE=4,
∴CD=8,
故答案为:C.
分析:连接OC,利用直径垂直平分弦以及勾股定理解出CD的长度。
5. D
∵∠AOB=∠_COD???
???_AB=CD,OA=OB=OC=OD,
∴△AOB≌△COD,
∴A、B、C成立,则D不成立,
故答案为:D21cnjy.com
分析:利用圆心角、弧、弦的关系定理,可证得AB=CD,弧AB=CD,再利用SSS可证得△AOB≌△COD,即可得出不一定成立的结论。21·cn·jy·com
二、填空题
6. 60
解:?∵弦AB把圆周分成1:5的两部分,
AB所对的圆心角度数为:
故答案为:60.
分析:由于弦AB把圆周分成1:5的两部分, 根据圆心角、弧、弦的关系得到弦AB所对的圆心角为圆周的.www.21-cn-jy.com
7. 68°
∵∠AOE=78°,∴劣弧 的度数为78°.
∵AB是⊙O的直径,∴劣弧 的度数为180°﹣78°=102°.
∵点C、D是弧BE的三等分点,∴∠COE 102°=68°.
故答案为:68°.
分析:根据∠AOE的度数求出劣弧 的度数,得到劣弧 的度数,根据圆心角、弧、弦的关系定理解答即可.2·1·c·n·j·y
8. 30
_è§???????_??§A_C与弧BD相等,
∴弧AB和弧CD相等,
∴∠2=∠1=30° ;
故答案为:30.
分析:由弧AC与弧BD相等推得弧AB和弧CD相等,再根据在同圆中,等弧所对的圆周角相等,从而求出∠2的度数.【来源:21·世纪·教育·网】
三、解答题
9. 证明:∵AD=BC,
∴ .
∴ .
∴ .
∴AB=CD
分析: 根据同圆中,相等的弦所对的弧相等得出?? , 进而根据等式的性质得出?, 最后根据等弧所对的弦相等即可得出AB=CD.21世纪教育网版权所有
10. 证明:∵AC=BD,
∴ .
∴
∴ .
∴AB=CD
分析:根据同圆中相等的弦所对的弧相等得出 ,根据等式的性质得出 ,根据同圆中相等的弧所对的弦相等得出AB=CD.21·世纪*教育网
_21?????????è?????(www.21cnjy.com)_
