2.3.1变量间的相关关系(共47张PPT)
文档属性
| 名称 | 2.3.1变量间的相关关系(共47张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 10:55:51 | ||
图片预览











文档简介
(共47张PPT)
变量间的相关关系(1)
2.如图所示的茎叶图记录了某班的甲、乙两名同学的五次800米训练成绩(单位:秒),通过茎叶图比较两人训练成绩的平均值及方差,并从中推荐一人参加运动会,①甲成绩的平均值高于乙成绩的平均值,推荐乙参加运动会.②甲成绩的平均值低于乙成绩的平均值,推荐甲参加运动会.③甲成绩的方差高于乙成绩的方差,推荐乙参加运动会.④甲成绩的方差低于乙成绩的方差,推荐甲参加运动会.其中正确结论的编号是( )
A.①③ B.②④ C.② D.③
A
A
A
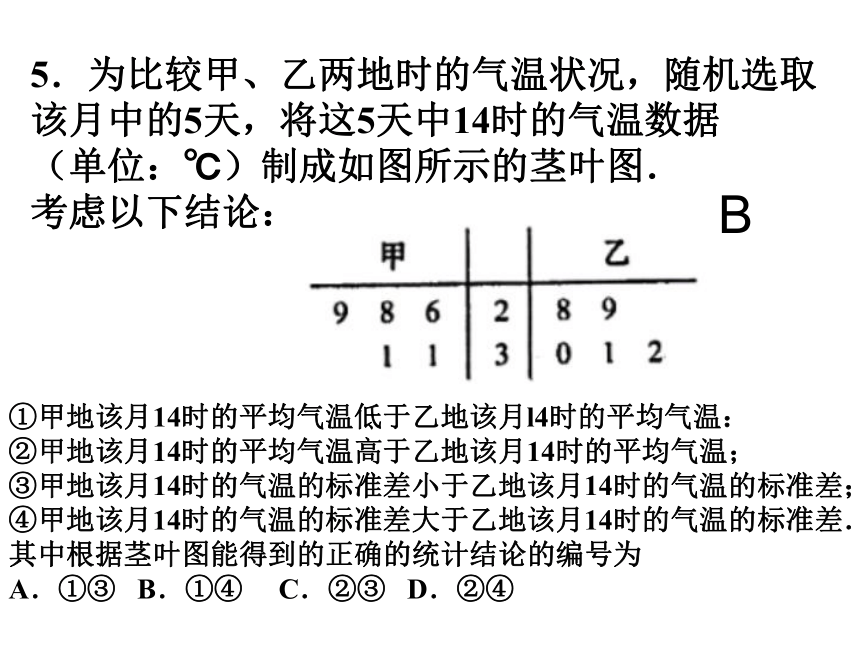
5.为比较甲、乙两地时的气温状况,随机选取
该月中的5天,将这5天中14时的气温数据
(单位:℃)制成如图所示的茎叶图.
考虑以下结论:
①甲地该月14时的平均气温低于乙地该月l4时的平均气温:
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的气温的标准差小于乙地该月14时的气温的标准差;
④甲地该月14时的气温的标准差大于乙地该月14时的气温的标准差.
其中根据茎叶图能得到的正确的统计结论的编号为
A.①③ B.①④ C.②③ D.②④
B
9.已知样本数据x1,x2,…xn的方差为4,则数据
2x1+3,2x2+3,…2xn+3的标准差是___________.
11.(2019·全国卷Ⅱ)演讲比赛共有9位评委分别给出某
选手的原始评分,评定该选手的成绩时,从9个原始评
分中去掉1个最高分、1个最低分,得到7个有效评分.7个
有效评分与9个原始评分相比,不变的数字特征是( )
A.中位数 B.平均数 C.方差 D.极差
4
A
解:(1)成绩在[70,80)内的频率为1-(0.005+0.010+0.020+0.035+0.005)×10=0.25,
所以60名学生中数学成绩在[70,80)内的人数为60×0.25=15.
(2)估计该校参加考试的学生数学成绩为优秀的人数为0.225×600=135.
(3)抽出的60名学生中分数在[40,70)内的频率为(0.005+0.010+0.020)×10=0.35,分数在[40,80)内的频率为(0.005+0.010+0.020+0.025)×10=0.6,所以中位数落在[70,80)内,故中位数为70+(1-0.05-0.1-0.2)/0.025=76.
14.甲、乙两人参加某体育项目训练,近期的五次测
试成绩得分情况如图所示.
(1)分别求出两人得分的平
均数与方差;
(2)根据折线图和(1)中
计算结果,对两人的
训练成绩作出评价.
变量间的相关关系(1)
1.姚明身高2.26米,很多人都在预测他们的孩子的身高也会很高.
2.很多人说: “数学成绩好的,物理成绩也不会太差”.
以上说法说法对吗?
事实上,我们在考察数学成绩对物理成绩影响的同时,还必须考虑到其他的因素对物理成绩的影响:爱好,努力程度
如果单纯从数学对物理的影响来考虑,就是考虑这两者之间的相关关系
物理成绩
数学成绩
学习兴趣
花费时间
其他因素
我们在生活中,碰到很多相关关系的问题:
1〉商品销售收入与广告支出经费之间的关系。
2〉粮食产量与施肥量之间的关系。
3〉人体内脂肪含量与年龄之间的关系。
随机性
函数关系
相关关系
1. 下列两个变量之间的关系不是函数关系 的是( ).
A. 某品牌手机的售价与销量
B. 地球上某地物体的重量与质量
C. 正方形的边长与面积
D. 铁球的直径与体积
A
2.下列两个变量之间的关系:
①角度和它的余弦值;
②正n边形的边数与内角和;
③家庭的支出与收入;
④某户家庭用电量与电价间的关系.
其中是相关关系的有( )
A.1个 B.2个
C.3个 D.4个
A
1、在一次对人体脂肪含量百分比和年龄的关系的研究中,研究人员获得了一组样本数据:
其中各年龄对应的脂肪数据是这个年龄人群脂肪含量的样本平均数.
思考:根据上述数据,人体的脂肪含量与年龄之间有怎样的关系?
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
为了确定年龄和人体脂肪含量之间的更明确的关系,我们需要对数据进行分析,通过作图可以对两个变量之间的关系有一个直观的印象.以x轴表示年龄,y轴表示脂肪含量,你能在直角坐标系中描出样本数据对应的图形吗?
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
下图叫做散点图,该如何给他下定义呢?
在平面直角坐标系中,表示具有相关关系的两个变量的一组数据图形,称为散点图.
在上面的散点图中,这些点散布在从左下角到右上角的区域,对于两个变量的这种相关关系,我们将它称为正相关.
2、下表是某小卖部6天卖出热茶的杯数与 当天气温的对比表:
气温/℃ 26 18 13 10 4 -1
杯数 20 24 34 38 50 64
(1)将上表中的数据制成散点图.
(2)由此你可得出什么结论?
在上面的散点图中,这些点散布在从左上角到右下角的区域,对于两个变量的这种相关关系,我们将它称为负相关.
1、如果散点图中的点散布在从左下角到右上角的区域,也就是说,从总体的变化规律来看,两个变量中的一个随另一个增大而增大,即两个变量的变化趋势相同。这种相关关系称为正相关。
2、如果散点图中的点散布在从左上角到右下角的区域。也就是说,从总体的变化规律来看,两个变量中的一个随另一个增大而减少,即两个变量的变化趋势相反。这种相关关系称为负相关。
正相关
负相关
练习:3、下列图形中两个变量具有相关关系的是( )
C
4、观察下列散点图,①正相关,②负相关,③不相关,与下列图形相对应的是( )
A.①②③ B.②③①
C.②①③ D.①③②
D
2,3
A
1、相关关系:
自变量取值一定时,因变量带有一定的随机性,而总体看又有一定的规律, 这种变量之间的关系称为相关关系
2、散点图
3、正相关、负相关
【典例】 某公司为了解用户对其产品的满意度,
从A,B两地区分别随机调查了40个用户,根据用
户对产品的满意度评分,得到A地区用户满意度评
分的频率分布直方图和B地区用户满意度评分的频
数分布表.
(1)作出B地区用户满意度评分的频率分布直方图,
并通过直方图比较两地区满意度评分的平均值及
分散程度(不要求计算出具体值,给出结论即可);
满意度评分分组 [50,60) [60,70) [70,80) [80,90) [90,100]
频数 2 8 14 10 6
[解] (1)通过两地区用户满意度评分的频率分布
直方图可以看出,B地区用户满意度评分的平均
值高于A地区用户满意度评分的平均值,B地区
用户满意度评分比较集中,而A地区用户满意度
评分比较分散.
(2)根据用户满意度评分,将用户的满意度分为三
个等级: 估计哪个地区用户的满意度等级为不满
意的概率大?说明理由.
满意度评分 低于70分 70分到89分 不低于90分
满意度等级 不满意 满意 非常满意
(2)A地区的用户的满意度等级为不满意的概率大.
记CA表示事件“A地区的用户的满意度等级为不
满意”;CB表示事件“B地区的用户的满意度等
级为不满意”.由直方图得P(CA)的估计值为
(0.01+0.02+0.03)×10=0.6,
P(CB)的估计值为(0.005+0.02)×10=0.25.
所以A地区的用户的满意度等级为不满意的
概率大.
变量间的相关关系(1)
2.如图所示的茎叶图记录了某班的甲、乙两名同学的五次800米训练成绩(单位:秒),通过茎叶图比较两人训练成绩的平均值及方差,并从中推荐一人参加运动会,①甲成绩的平均值高于乙成绩的平均值,推荐乙参加运动会.②甲成绩的平均值低于乙成绩的平均值,推荐甲参加运动会.③甲成绩的方差高于乙成绩的方差,推荐乙参加运动会.④甲成绩的方差低于乙成绩的方差,推荐甲参加运动会.其中正确结论的编号是( )
A.①③ B.②④ C.② D.③
A
A
A
5.为比较甲、乙两地时的气温状况,随机选取
该月中的5天,将这5天中14时的气温数据
(单位:℃)制成如图所示的茎叶图.
考虑以下结论:
①甲地该月14时的平均气温低于乙地该月l4时的平均气温:
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的气温的标准差小于乙地该月14时的气温的标准差;
④甲地该月14时的气温的标准差大于乙地该月14时的气温的标准差.
其中根据茎叶图能得到的正确的统计结论的编号为
A.①③ B.①④ C.②③ D.②④
B
9.已知样本数据x1,x2,…xn的方差为4,则数据
2x1+3,2x2+3,…2xn+3的标准差是___________.
11.(2019·全国卷Ⅱ)演讲比赛共有9位评委分别给出某
选手的原始评分,评定该选手的成绩时,从9个原始评
分中去掉1个最高分、1个最低分,得到7个有效评分.7个
有效评分与9个原始评分相比,不变的数字特征是( )
A.中位数 B.平均数 C.方差 D.极差
4
A
解:(1)成绩在[70,80)内的频率为1-(0.005+0.010+0.020+0.035+0.005)×10=0.25,
所以60名学生中数学成绩在[70,80)内的人数为60×0.25=15.
(2)估计该校参加考试的学生数学成绩为优秀的人数为0.225×600=135.
(3)抽出的60名学生中分数在[40,70)内的频率为(0.005+0.010+0.020)×10=0.35,分数在[40,80)内的频率为(0.005+0.010+0.020+0.025)×10=0.6,所以中位数落在[70,80)内,故中位数为70+(1-0.05-0.1-0.2)/0.025=76.
14.甲、乙两人参加某体育项目训练,近期的五次测
试成绩得分情况如图所示.
(1)分别求出两人得分的平
均数与方差;
(2)根据折线图和(1)中
计算结果,对两人的
训练成绩作出评价.
变量间的相关关系(1)
1.姚明身高2.26米,很多人都在预测他们的孩子的身高也会很高.
2.很多人说: “数学成绩好的,物理成绩也不会太差”.
以上说法说法对吗?
事实上,我们在考察数学成绩对物理成绩影响的同时,还必须考虑到其他的因素对物理成绩的影响:爱好,努力程度
如果单纯从数学对物理的影响来考虑,就是考虑这两者之间的相关关系
物理成绩
数学成绩
学习兴趣
花费时间
其他因素
我们在生活中,碰到很多相关关系的问题:
1〉商品销售收入与广告支出经费之间的关系。
2〉粮食产量与施肥量之间的关系。
3〉人体内脂肪含量与年龄之间的关系。
随机性
函数关系
相关关系
1. 下列两个变量之间的关系不是函数关系 的是( ).
A. 某品牌手机的售价与销量
B. 地球上某地物体的重量与质量
C. 正方形的边长与面积
D. 铁球的直径与体积
A
2.下列两个变量之间的关系:
①角度和它的余弦值;
②正n边形的边数与内角和;
③家庭的支出与收入;
④某户家庭用电量与电价间的关系.
其中是相关关系的有( )
A.1个 B.2个
C.3个 D.4个
A
1、在一次对人体脂肪含量百分比和年龄的关系的研究中,研究人员获得了一组样本数据:
其中各年龄对应的脂肪数据是这个年龄人群脂肪含量的样本平均数.
思考:根据上述数据,人体的脂肪含量与年龄之间有怎样的关系?
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
为了确定年龄和人体脂肪含量之间的更明确的关系,我们需要对数据进行分析,通过作图可以对两个变量之间的关系有一个直观的印象.以x轴表示年龄,y轴表示脂肪含量,你能在直角坐标系中描出样本数据对应的图形吗?
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
下图叫做散点图,该如何给他下定义呢?
在平面直角坐标系中,表示具有相关关系的两个变量的一组数据图形,称为散点图.
在上面的散点图中,这些点散布在从左下角到右上角的区域,对于两个变量的这种相关关系,我们将它称为正相关.
2、下表是某小卖部6天卖出热茶的杯数与 当天气温的对比表:
气温/℃ 26 18 13 10 4 -1
杯数 20 24 34 38 50 64
(1)将上表中的数据制成散点图.
(2)由此你可得出什么结论?
在上面的散点图中,这些点散布在从左上角到右下角的区域,对于两个变量的这种相关关系,我们将它称为负相关.
1、如果散点图中的点散布在从左下角到右上角的区域,也就是说,从总体的变化规律来看,两个变量中的一个随另一个增大而增大,即两个变量的变化趋势相同。这种相关关系称为正相关。
2、如果散点图中的点散布在从左上角到右下角的区域。也就是说,从总体的变化规律来看,两个变量中的一个随另一个增大而减少,即两个变量的变化趋势相反。这种相关关系称为负相关。
正相关
负相关
练习:3、下列图形中两个变量具有相关关系的是( )
C
4、观察下列散点图,①正相关,②负相关,③不相关,与下列图形相对应的是( )
A.①②③ B.②③①
C.②①③ D.①③②
D
2,3
A
1、相关关系:
自变量取值一定时,因变量带有一定的随机性,而总体看又有一定的规律, 这种变量之间的关系称为相关关系
2、散点图
3、正相关、负相关
【典例】 某公司为了解用户对其产品的满意度,
从A,B两地区分别随机调查了40个用户,根据用
户对产品的满意度评分,得到A地区用户满意度评
分的频率分布直方图和B地区用户满意度评分的频
数分布表.
(1)作出B地区用户满意度评分的频率分布直方图,
并通过直方图比较两地区满意度评分的平均值及
分散程度(不要求计算出具体值,给出结论即可);
满意度评分分组 [50,60) [60,70) [70,80) [80,90) [90,100]
频数 2 8 14 10 6
[解] (1)通过两地区用户满意度评分的频率分布
直方图可以看出,B地区用户满意度评分的平均
值高于A地区用户满意度评分的平均值,B地区
用户满意度评分比较集中,而A地区用户满意度
评分比较分散.
(2)根据用户满意度评分,将用户的满意度分为三
个等级: 估计哪个地区用户的满意度等级为不满
意的概率大?说明理由.
满意度评分 低于70分 70分到89分 不低于90分
满意度等级 不满意 满意 非常满意
(2)A地区的用户的满意度等级为不满意的概率大.
记CA表示事件“A地区的用户的满意度等级为不
满意”;CB表示事件“B地区的用户的满意度等
级为不满意”.由直方图得P(CA)的估计值为
(0.01+0.02+0.03)×10=0.6,
P(CB)的估计值为(0.005+0.02)×10=0.25.
所以A地区的用户的满意度等级为不满意的
概率大.
