2020春人教版八下数学第18.1.2平行四边形的判定同步课堂练习(共2课时、含答案)
文档属性
| 名称 | 2020春人教版八下数学第18.1.2平行四边形的判定同步课堂练习(共2课时、含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 102.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-18 18:15:42 | ||
图片预览


文档简介
2020春人教版八下数学第18.1.2平行四边形的判定同步课堂练习
18.1.2平行四边形的判定(1)
1.下列条件中,能够判别出四边形ABCD是平行四边形的是( )
A.AB=BC=CD
B.∠B+∠C=180°,∠C+∠D=180°
C.AB=BC,CD=DA
D.∠A+∠B=180°,∠C+∠D=180°
2.如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( )
A.6
B.12
C.20
D.24
3.四边形ABCD中,已知AD∥BC,要使四边形ABCD为平行四边形,需要增加条件 .
4.在四边形ABCD中,AB=CD,BC=AD.求证:四边形ABCD是平行四边形(用定义证明).
5.如图,在?ABCD中,E、F是边BC、DA上的两点,且AE∥CF.求证:AE=CF.
6.如图,四边形ABCD的对角线AC、BD相交于O点,且OA=OC,OB=OD.求证:四边形ABCD是平行四边形(用定义证明).
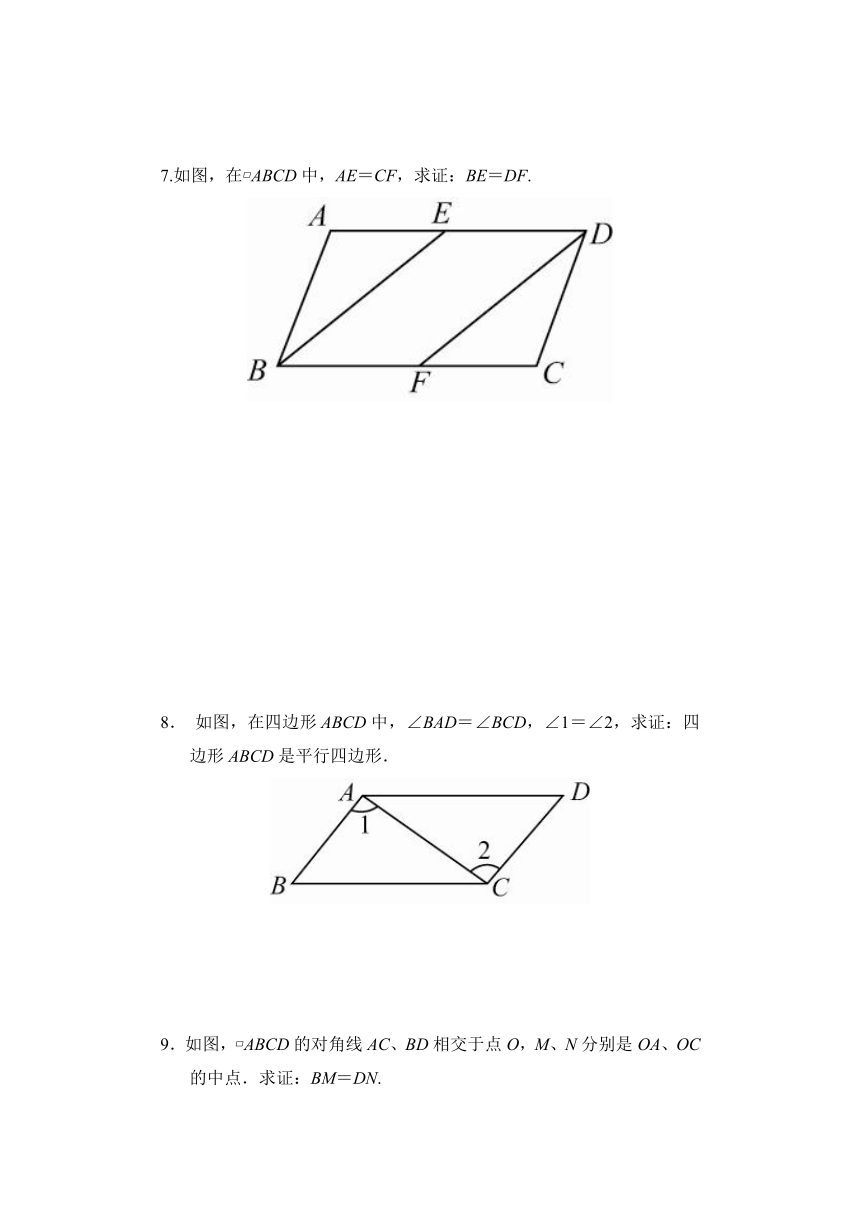
7.如图,在?ABCD中,AE=CF,求证:BE=DF.
8. 如图,在四边形ABCD中,∠BAD=∠BCD,∠1=∠2,求证:四边形ABCD是平行四边形.
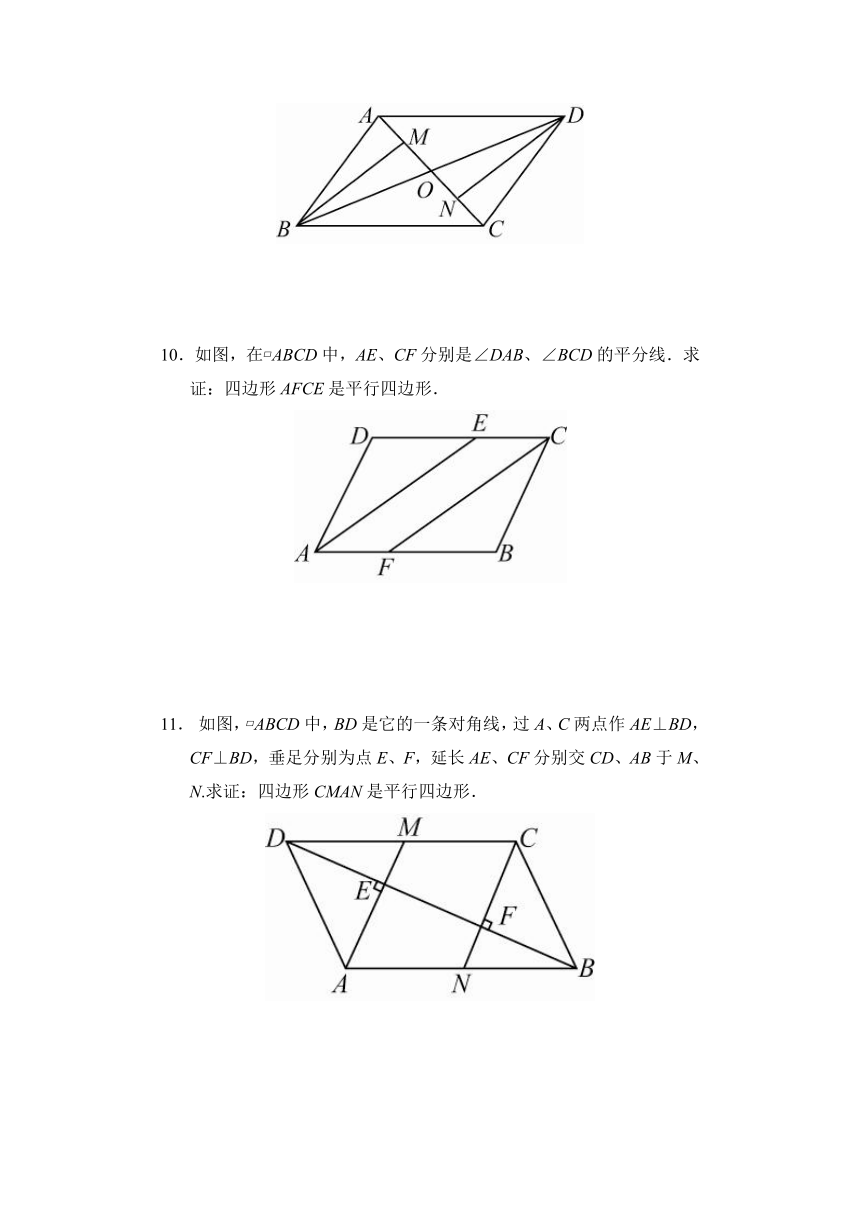
9.如图,?ABCD的对角线AC、BD相交于点O,M、N分别是OA、OC的中点.求证:BM=DN.
10.如图,在?ABCD中,AE、CF分别是∠DAB、∠BCD的平分线.求证:四边形AFCE是平行四边形.
11. 如图,?ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为点E、F,延长AE、CF分别交CD、AB于M、N.求证:四边形CMAN是平行四边形.
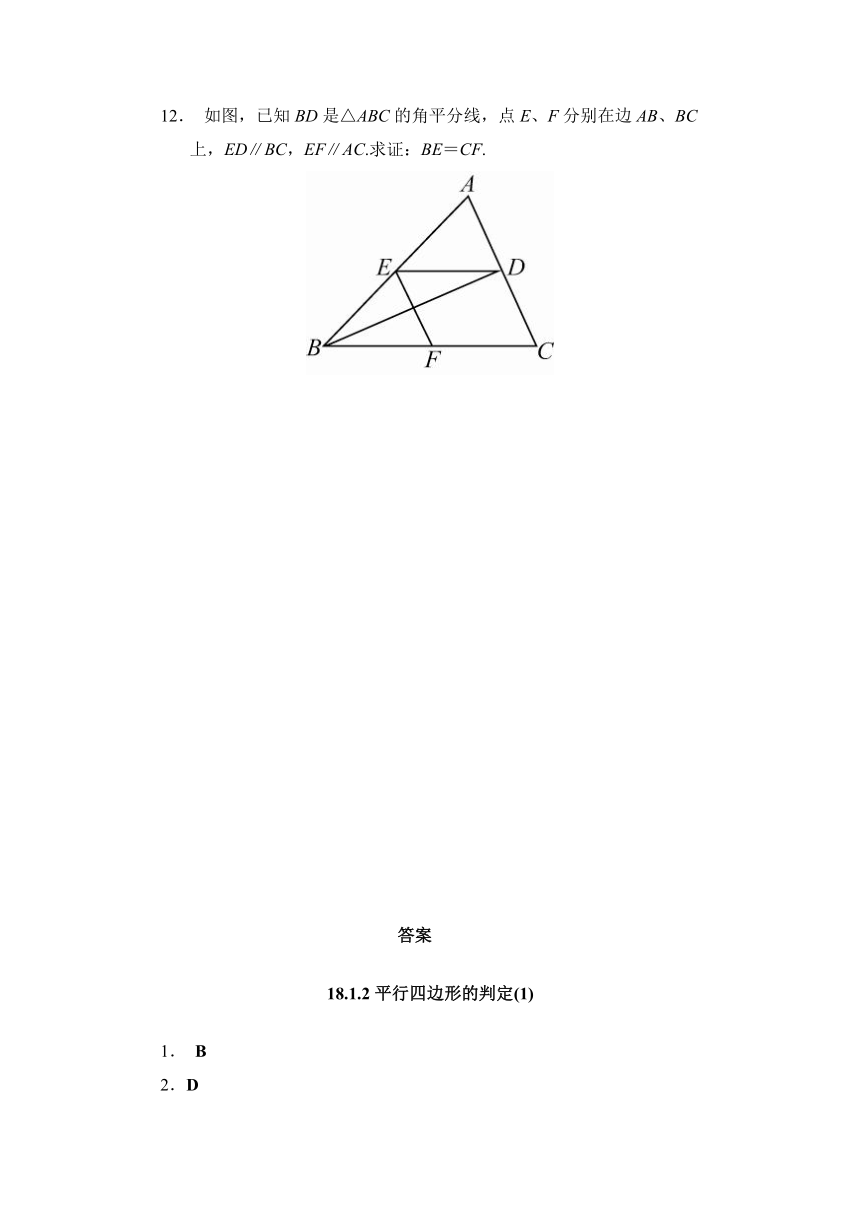
12. 如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,EF∥AC.求证:BE=CF.
答案
18.1.2平行四边形的判定(1)
1. B
2.D
3. AB∥CD或∠A=∠C或∠B=∠D.
4. 证明:连接AC,∵AB=CD,
BC=AD,
AC=AC.
∴△ABC≌△CDA(SSS),
∴∠DAC=∠ACB,∠ACD=∠BAC,
∴AD∥BC,AB∥DC,
∴四边形ABCD为平行四边形.
5. 证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
又∵E、F是边BC、DA上的两点,
∴AF∥EC,∵AE∥CF,
∴四边形AECF是平行四边形,
∴AE=CF.
6. 证明:∵OA=OC,OB=OD,且∠AOD=∠COB(对顶角相等),
∴△AOD≌△COB(SAS),
∴∠DAO=∠BCO,
∴AD∥BC.同理可得
∴△AOB≌△COD,AB∥DC,
∴四边形ABCD为平行四边形.
7. 证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
AD=BC,
∵AE=CF,
∴DE=BF,DE∥BF,
∴四边形DEBF是平行四边形,
∴BE=DF.
8. 证明:∵∠1=∠2,
∴AB∥CD,
∵∠BAD=∠BCD
∴∠BAD-∠1=∠BCD-∠2,
∴∠CAD=∠BCA,∴AD∥BC,
∴四边形ABCD是平行四边形.
9. 证明:连接BN、DM,
∵四边形ABCD是平行四边形,
∴AO=CO,
BO=DO,
又∵M、N分别是OA、OC的中点,
∴OM=ON=OA=OC,
∴四边形MBND是平行四边形,∴BM=DN.
10. 证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∠DAB=∠DCB,
∵AE、CF分别是∠DAB、∠BCD的平分线,
∴∠EAB=∠DCF=∠DAB
=∠DCB,∠CFB=∠DCF,
∴∠EAB=∠CFB,
∴AE∥CF,又∵EC∥AF(AB∥CD),
∴四边形AFCE是平行四边形.
11. 证明:∵AE⊥BD,CF⊥BD,
∴AE∥CF,
又∵四边形ABCD是平行四边形,
∴AB∥CD,
∴四边形CMAN是平行四边形.
12. 证明:∵ED∥BC,EF∥AC,
∴四边形EFCD是平行四边形,
∴DE=CF,
∵BD平分∠ABC,
∴∠EBD=∠DBC,∵DE∥BC,
∴∠EDB=∠DBC,∴∠EBD=∠EDB,
∴EB=ED,∴BE=CF.
18.1.2平行四边形的判定(2)
1. 下列真命题的个数有( )
①对角线互相平分的四边形是平行四边形;
②两组对角分别相等的四边形是平行四边形;
③一组对边平行,另一组对边相等的四边形是平行四边形.
A.3个 B.2个 C.1个 D.0个
2. 如图所示,四边形ABCD的对角线相交于点O,若AB∥CD,请添加一个条件 (写一个即可),使四边形ABCD是平行四边形.
3.如图,在?ABCD中,E、F分别是AD、BC的中点.
求证:四边形BFDE是平行四边形.
4. 如图,在?ABCD中,点E,F在对角线AC上,且AE=CF.求证:
(1)DE=BF;
(2)四边形DEBF是平行四边形.
5.已知:在?ABCD中,BE=DF.
求证:四边形AECF是平行四边形.
6. 如图,E、F是平行四边形ABCD的对角线AC上的点,CE=AF.求证:四边形BEDF是平行四边形.
7.如图,DE⊥AC,BF⊥AC,DE=BF,且∠ADB=∠DBC.求证:四边形ABCD是平行四边形.
8. 如图,E,F为?ABCD对角线AC上的两点,且AE=CF,连接BE,DF,求证:BE=DF.
9.如图,在△ABC中,AB=AC,点E在AB上,D是BC的中点,EB=ED,延长ED到F,使ED=FD,连接FC.求证:四边形AEFC是平行四边形.
10. 如图,在?ABCD中,E,F分别为边AD,BC的中点,对角线AC分别交BE,DF于点G,H.求证:AG=CH.
11. 如图,在?ABCD中,点E,F分别在AD,BC上,且AE=CF,EF,BD相交于点O,求证:OE=OF.
答案
1. B
2. AD∥BC(答案不唯一)
3. 证明:∵?ABCD,
∴AD=BC,
且AD∥BC,
∵E、F分别是AD、BC的中点,∴DE=BF,且DE∥BF,
∴四边形BFDE是平行四边形.
4. 证明:(1)∵四边形ABCD是平行四边形,
∴AD∥CB,
AD=CB,∴∠DAE=∠BCF,
在△ADE和△CBF中,
∴△ADE≌△CBF,∴DE=BF.
(2)由(1),可得△ADE≌△CBF,
∴∠ADE=∠CBF,
∵∠DEF=∠DAE+∠ADE,
∠BFE=∠BCF+∠CBF,
∴∠DEF=∠BFE,∴DE∥BF,
又∵DE=BF,∴四边形DEBF是平行四边形.
5. 证明:∵?ABCD,
∴AB=DC,
且AB∥DC,
∵BE=DF,∴AE=CF,且AE∥CF,
∴四边形AECF是平行四边形.
6.证明:∵CE=AF,
∴CE-EF=AF-EF
即AE=CF,
如图:连接BD交AC于O,
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO
∵AE=CF,
∴AO-AE=CO-CF.
即EO=FO.
∴四边形BEDF为平行四边形(对角线互相平分的四边形是平行四边形).
7. 证明:∵∠ADB=∠DBC,
∴AD∥BC,
∴∠DAE=∠BCF,
∵DE⊥AC,BF⊥AC,
∴∠DEA=∠BFC=90°,
又∵DE=BF,
∴△ADE≌△CBF(AAS),
∴AD=BC,
∴四边形ABCD是平行四边形.
8. 证明:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC.
∴∠BAE=∠DCF.
在△AEB和△CFD中,
∴△AEB≌△CFD(SAS).
∴BE=DF.
9. 证明:先证△EBD≌△FCD,
∴∠ABC=∠BCF,
∴AB∥CF,∵EB=ED,AB=AC,
∴∠B=∠EDB,∠B=∠ACB,
∴EF∥AC,
∴四边形AEFC是平行四边形.
10. 证明:∵E,F分别是AD,BC的中点,
∴AE=DE=AD,CF=BF=BC.
又∵AD∥BC,且AD=BC.
∴DE∥BF,且DE=BF.
∴四边形BEDF是平行四边形.
∴∠BED=∠DFB.
∴∠AEG=∠DFC,又∵AD∥BC,
∴∠EAG=∠FCH.
在△AGE和△CHF中,
∴△AGE≌△CHF.∴AG=CH.
11. 证明:连接BE、DF,
如图所示:
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∵AE=CF,∴DE=BF,
∴四边形BEDF是平行四边形,∴OF=OE.
18.1.2平行四边形的判定(1)
1.下列条件中,能够判别出四边形ABCD是平行四边形的是( )
A.AB=BC=CD
B.∠B+∠C=180°,∠C+∠D=180°
C.AB=BC,CD=DA
D.∠A+∠B=180°,∠C+∠D=180°
2.如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( )
A.6
B.12
C.20
D.24
3.四边形ABCD中,已知AD∥BC,要使四边形ABCD为平行四边形,需要增加条件 .
4.在四边形ABCD中,AB=CD,BC=AD.求证:四边形ABCD是平行四边形(用定义证明).
5.如图,在?ABCD中,E、F是边BC、DA上的两点,且AE∥CF.求证:AE=CF.
6.如图,四边形ABCD的对角线AC、BD相交于O点,且OA=OC,OB=OD.求证:四边形ABCD是平行四边形(用定义证明).
7.如图,在?ABCD中,AE=CF,求证:BE=DF.
8. 如图,在四边形ABCD中,∠BAD=∠BCD,∠1=∠2,求证:四边形ABCD是平行四边形.
9.如图,?ABCD的对角线AC、BD相交于点O,M、N分别是OA、OC的中点.求证:BM=DN.
10.如图,在?ABCD中,AE、CF分别是∠DAB、∠BCD的平分线.求证:四边形AFCE是平行四边形.
11. 如图,?ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为点E、F,延长AE、CF分别交CD、AB于M、N.求证:四边形CMAN是平行四边形.
12. 如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,EF∥AC.求证:BE=CF.
答案
18.1.2平行四边形的判定(1)
1. B
2.D
3. AB∥CD或∠A=∠C或∠B=∠D.
4. 证明:连接AC,∵AB=CD,
BC=AD,
AC=AC.
∴△ABC≌△CDA(SSS),
∴∠DAC=∠ACB,∠ACD=∠BAC,
∴AD∥BC,AB∥DC,
∴四边形ABCD为平行四边形.
5. 证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
又∵E、F是边BC、DA上的两点,
∴AF∥EC,∵AE∥CF,
∴四边形AECF是平行四边形,
∴AE=CF.
6. 证明:∵OA=OC,OB=OD,且∠AOD=∠COB(对顶角相等),
∴△AOD≌△COB(SAS),
∴∠DAO=∠BCO,
∴AD∥BC.同理可得
∴△AOB≌△COD,AB∥DC,
∴四边形ABCD为平行四边形.
7. 证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
AD=BC,
∵AE=CF,
∴DE=BF,DE∥BF,
∴四边形DEBF是平行四边形,
∴BE=DF.
8. 证明:∵∠1=∠2,
∴AB∥CD,
∵∠BAD=∠BCD
∴∠BAD-∠1=∠BCD-∠2,
∴∠CAD=∠BCA,∴AD∥BC,
∴四边形ABCD是平行四边形.
9. 证明:连接BN、DM,
∵四边形ABCD是平行四边形,
∴AO=CO,
BO=DO,
又∵M、N分别是OA、OC的中点,
∴OM=ON=OA=OC,
∴四边形MBND是平行四边形,∴BM=DN.
10. 证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∠DAB=∠DCB,
∵AE、CF分别是∠DAB、∠BCD的平分线,
∴∠EAB=∠DCF=∠DAB
=∠DCB,∠CFB=∠DCF,
∴∠EAB=∠CFB,
∴AE∥CF,又∵EC∥AF(AB∥CD),
∴四边形AFCE是平行四边形.
11. 证明:∵AE⊥BD,CF⊥BD,
∴AE∥CF,
又∵四边形ABCD是平行四边形,
∴AB∥CD,
∴四边形CMAN是平行四边形.
12. 证明:∵ED∥BC,EF∥AC,
∴四边形EFCD是平行四边形,
∴DE=CF,
∵BD平分∠ABC,
∴∠EBD=∠DBC,∵DE∥BC,
∴∠EDB=∠DBC,∴∠EBD=∠EDB,
∴EB=ED,∴BE=CF.
18.1.2平行四边形的判定(2)
1. 下列真命题的个数有( )
①对角线互相平分的四边形是平行四边形;
②两组对角分别相等的四边形是平行四边形;
③一组对边平行,另一组对边相等的四边形是平行四边形.
A.3个 B.2个 C.1个 D.0个
2. 如图所示,四边形ABCD的对角线相交于点O,若AB∥CD,请添加一个条件 (写一个即可),使四边形ABCD是平行四边形.
3.如图,在?ABCD中,E、F分别是AD、BC的中点.
求证:四边形BFDE是平行四边形.
4. 如图,在?ABCD中,点E,F在对角线AC上,且AE=CF.求证:
(1)DE=BF;
(2)四边形DEBF是平行四边形.
5.已知:在?ABCD中,BE=DF.
求证:四边形AECF是平行四边形.
6. 如图,E、F是平行四边形ABCD的对角线AC上的点,CE=AF.求证:四边形BEDF是平行四边形.
7.如图,DE⊥AC,BF⊥AC,DE=BF,且∠ADB=∠DBC.求证:四边形ABCD是平行四边形.
8. 如图,E,F为?ABCD对角线AC上的两点,且AE=CF,连接BE,DF,求证:BE=DF.
9.如图,在△ABC中,AB=AC,点E在AB上,D是BC的中点,EB=ED,延长ED到F,使ED=FD,连接FC.求证:四边形AEFC是平行四边形.
10. 如图,在?ABCD中,E,F分别为边AD,BC的中点,对角线AC分别交BE,DF于点G,H.求证:AG=CH.
11. 如图,在?ABCD中,点E,F分别在AD,BC上,且AE=CF,EF,BD相交于点O,求证:OE=OF.
答案
1. B
2. AD∥BC(答案不唯一)
3. 证明:∵?ABCD,
∴AD=BC,
且AD∥BC,
∵E、F分别是AD、BC的中点,∴DE=BF,且DE∥BF,
∴四边形BFDE是平行四边形.
4. 证明:(1)∵四边形ABCD是平行四边形,
∴AD∥CB,
AD=CB,∴∠DAE=∠BCF,
在△ADE和△CBF中,
∴△ADE≌△CBF,∴DE=BF.
(2)由(1),可得△ADE≌△CBF,
∴∠ADE=∠CBF,
∵∠DEF=∠DAE+∠ADE,
∠BFE=∠BCF+∠CBF,
∴∠DEF=∠BFE,∴DE∥BF,
又∵DE=BF,∴四边形DEBF是平行四边形.
5. 证明:∵?ABCD,
∴AB=DC,
且AB∥DC,
∵BE=DF,∴AE=CF,且AE∥CF,
∴四边形AECF是平行四边形.
6.证明:∵CE=AF,
∴CE-EF=AF-EF
即AE=CF,
如图:连接BD交AC于O,
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO
∵AE=CF,
∴AO-AE=CO-CF.
即EO=FO.
∴四边形BEDF为平行四边形(对角线互相平分的四边形是平行四边形).
7. 证明:∵∠ADB=∠DBC,
∴AD∥BC,
∴∠DAE=∠BCF,
∵DE⊥AC,BF⊥AC,
∴∠DEA=∠BFC=90°,
又∵DE=BF,
∴△ADE≌△CBF(AAS),
∴AD=BC,
∴四边形ABCD是平行四边形.
8. 证明:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC.
∴∠BAE=∠DCF.
在△AEB和△CFD中,
∴△AEB≌△CFD(SAS).
∴BE=DF.
9. 证明:先证△EBD≌△FCD,
∴∠ABC=∠BCF,
∴AB∥CF,∵EB=ED,AB=AC,
∴∠B=∠EDB,∠B=∠ACB,
∴EF∥AC,
∴四边形AEFC是平行四边形.
10. 证明:∵E,F分别是AD,BC的中点,
∴AE=DE=AD,CF=BF=BC.
又∵AD∥BC,且AD=BC.
∴DE∥BF,且DE=BF.
∴四边形BEDF是平行四边形.
∴∠BED=∠DFB.
∴∠AEG=∠DFC,又∵AD∥BC,
∴∠EAG=∠FCH.
在△AGE和△CHF中,
∴△AGE≌△CHF.∴AG=CH.
11. 证明:连接BE、DF,
如图所示:
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∵AE=CF,∴DE=BF,
∴四边形BEDF是平行四边形,∴OF=OE.
