北师大版数学七年级下册第2章《相交线与平行线》单元检测题(含详细答案)
文档属性
| 名称 | 北师大版数学七年级下册第2章《相交线与平行线》单元检测题(含详细答案) |  | |
| 格式 | zip | ||
| 文件大小 | 237.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-18 19:04:46 | ||
图片预览

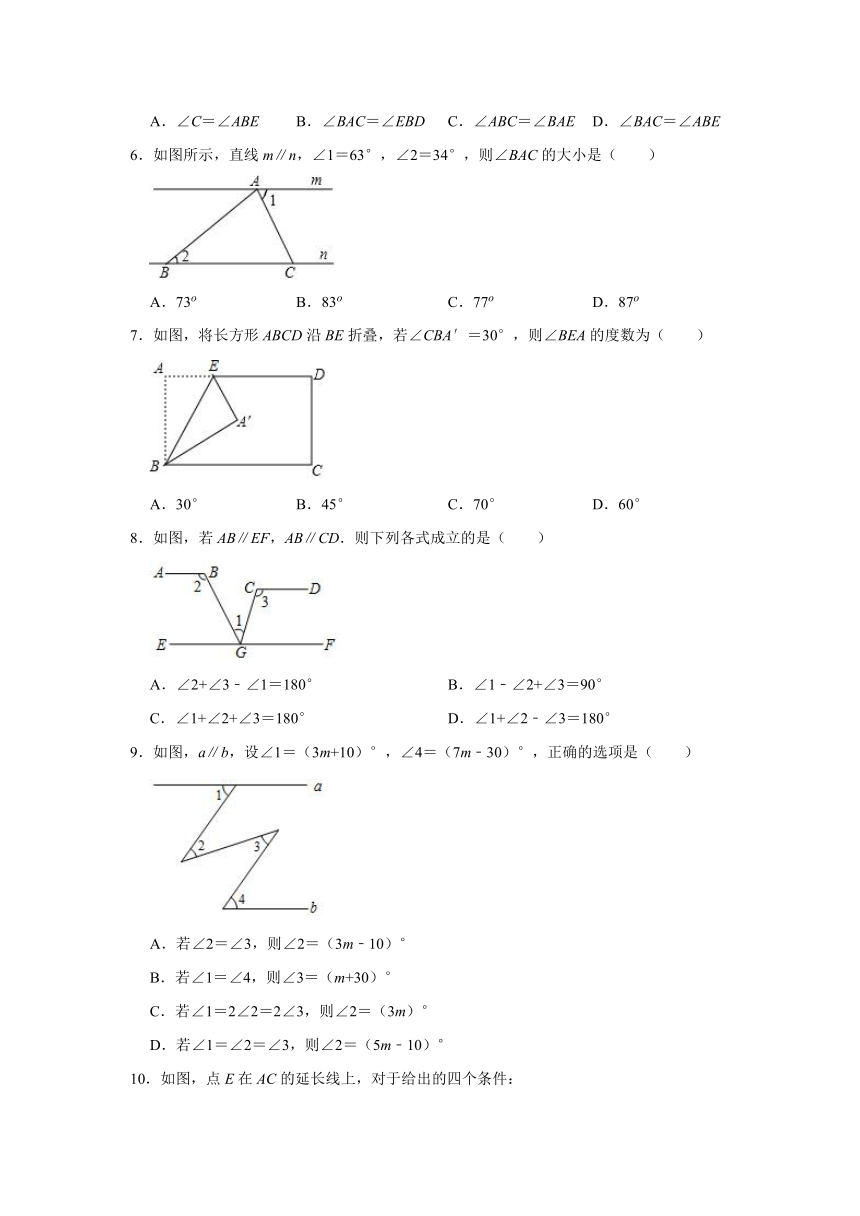

文档简介
北师大版七年级下册第2章《相交线与平行线》单元检测题
检测时间100分钟 满分120分
姓名________班级________学号________分数________
一.选择题(共10小题,满分30分)
1.下列图形中,∠1与∠2互为对顶角的是( )
A. B.
C. D.
2.平面内两两相交的3条直线,其交点个数最少为m个,最多为n个,则m+n等于( )
A.4 B.5 C.6 D.以上都不对
3.有下列画图语句:
①画出线段A,B的中点;
②画出A,B两点的距离;
③延长射线OP;
④连接A,B两点,其中正确的个数是( )
A.1 B.2 C.3 D.4
4.如图,直线AB、CD相交于点O,∠EOD=90°.下列说法不正确的是( )
A.∠AOD=∠BOC B.∠AOC=∠AOE
C.∠AOE+∠BOD=90° D.∠AOD+∠BOD=180°
5.如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE B.∠BAC=∠EBD C.∠ABC=∠BAE D.∠BAC=∠ABE
6.如图所示,直线m∥n,∠1=63°,∠2=34°,则∠BAC的大小是( )
A.73o B.83o C.77o D.87o
7.如图,将长方形ABCD沿BE折叠,若∠CBA′=30°,则∠BEA的度数为( )
A.30° B.45° C.70° D.60°
8.如图,若AB∥EF,AB∥CD.则下列各式成立的是( )
A.∠2+∠3﹣∠1=180° B.∠1﹣∠2+∠3=90°
C.∠1+∠2+∠3=180° D.∠1+∠2﹣∠3=180°
9.如图,a∥b,设∠1=(3m+10)°,∠4=(7m﹣30)°,正确的选项是( )
A.若∠2=∠3,则∠2=(3m﹣10)°
B.若∠1=∠4,则∠3=(m+30)°
C.若∠1=2∠2=2∠3,则∠2=(3m)°
D.若∠1=∠2=∠3,则∠2=(5m﹣10)°
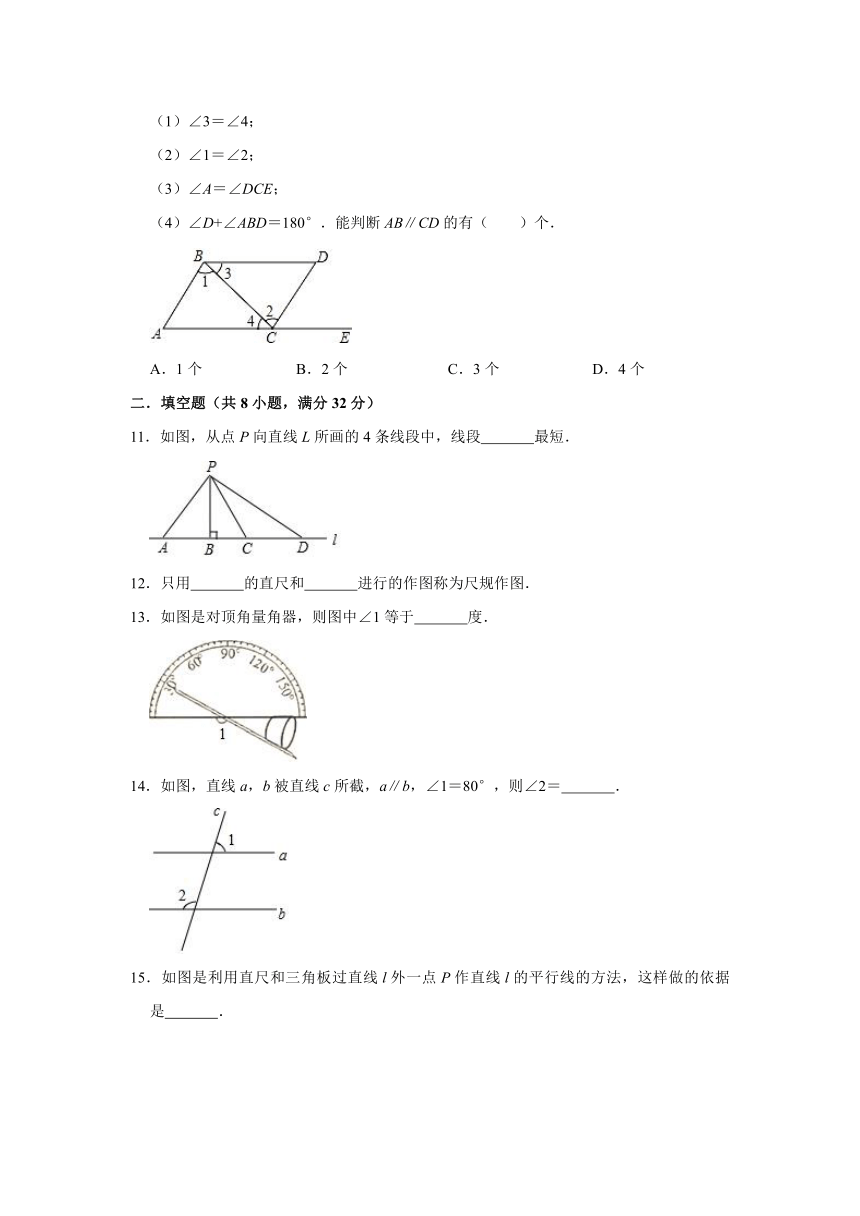
10.如图,点E在AC的延长线上,对于给出的四个条件:
(1)∠3=∠4;
(2)∠1=∠2;
(3)∠A=∠DCE;
(4)∠D+∠ABD=180°.能判断AB∥CD的有( )个.
A.1个 B.2个 C.3个 D.4个
二.填空题(共8小题,满分32分)
11.如图,从点P向直线L所画的4条线段中,线段 最短.
12.只用 的直尺和 进行的作图称为尺规作图.
13.如图是对顶角量角器,则图中∠1等于 度.
14.如图,直线a,b被直线c所截,a∥b,∠1=80°,则∠2= .
15.如图是利用直尺和三角板过直线l外一点P作直线l的平行线的方法,这样做的依据是 .
16.如图,已知AB∥CD∥EF,则∠1,∠2,∠3之间的数量关系是 .
17.直线AB与CD相交于点O,∠AOC=50°,若∠EOD=20°,则∠BOE= .
18.如图,点A,B,C,D在同一直线上,BF平分∠EBD,CG∥BF,若∠EBA=α°,则∠GCD= °(用关于α的代数式表示)
三.解答题(共7小题,满分58分)
19.如图所示,已知AD∥BC,BE平分∠ABC,∠A=110°.求∠ADB的度数.
20.如图,三条直线AB、CD、EF共点于O,三个交角的关系是∠3=3∠2、∠2=2∠1,求∠1、∠2、∠3的大小.
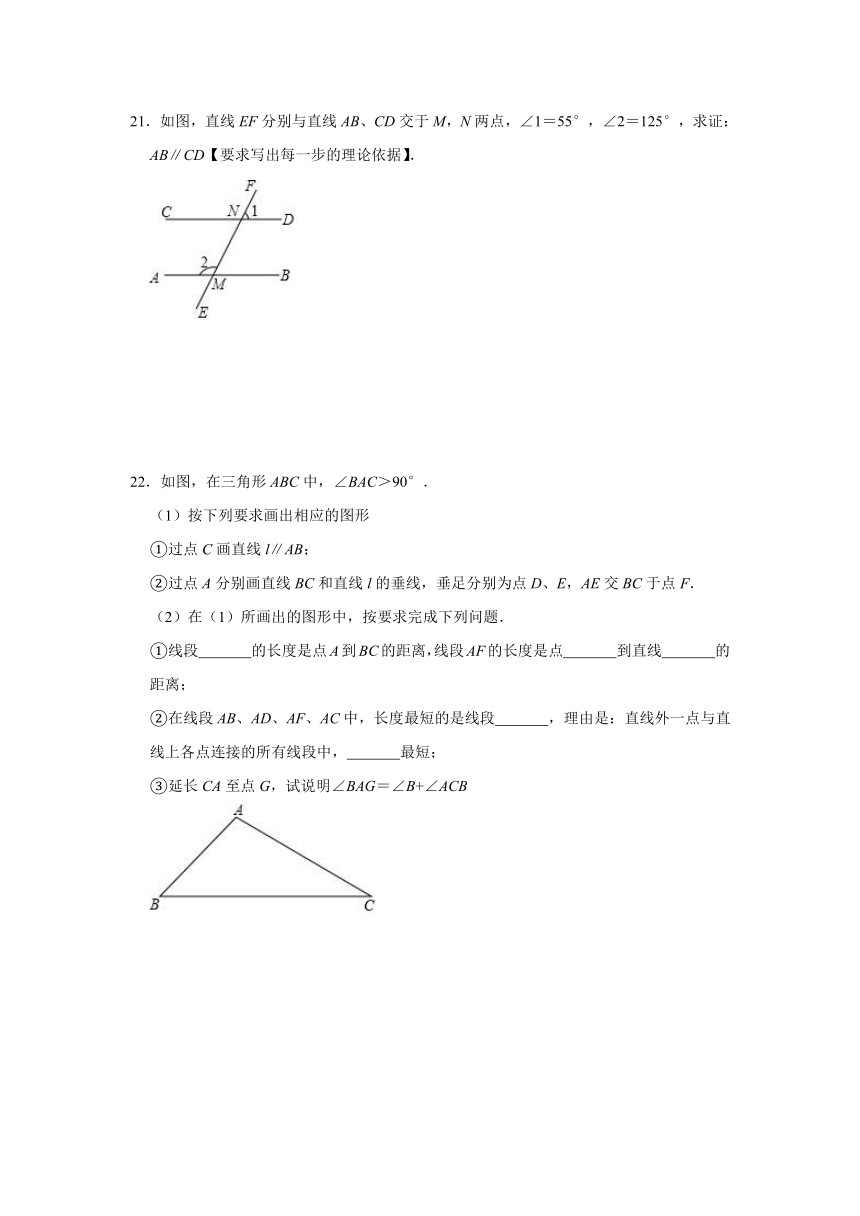
21.如图,直线EF分别与直线AB、CD交于M,N两点,∠1=55°,∠2=125°,求证:AB∥CD【要求写出每一步的理论依据】.
22.如图,在三角形ABC中,∠BAC>90°.
(1)按下列要求画出相应的图形
①过点C画直线l∥AB;
②过点A分别画直线BC和直线l的垂线,垂足分别为点D、E,AE交BC于点F.
(2)在(1)所画出的图形中,按要求完成下列问题.
①线段 的长度是点A到BC的距离,线段AF的长度是点 到直线 的距离;
②在线段AB、AD、AF、AC中,长度最短的是线段 ,理由是:直线外一点与直线上各点连接的所有线段中, 最短;
③延长CA至点G,试说明∠BAG=∠B+∠ACB
23.如图,直线EF、CD相交于点O,∠AOB=90°,OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=30°,请直接写出∠BOD的度数;
(3)观察(1)、(2)的结果,猜想∠AOE和∠BOD的数量关系,并说明理由.
24.如图,已知AM∥BN,∠A=64°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)①∠ABN的度数是 ;②∵AM∥BN,∴∠ACB=∠ ;
(2)求∠CBD的度数;
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由:若变化,请写出变化规律;
(4)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .
25.课题学习:平行线的“等角转化功能.
(1)问题情景:如图1,已知点A是BC外一点,连接AB、AC,求∠BAC+∠B+∠C的度数.
天天同学看过图形后立即想出:∠BAC+∠B+∠C=180°,请你补全他的推理过程.
解:(1)如图1,过点A作ED∥BC,∴∠B= ,∠C= .
又∵∠EAB+∠BAC+∠CAD=180°,∴∠BAC+∠B+∠C=180°.
解题反思:从上面的推理过程中,我们发现平行线具有“等角转化”功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决.
(2)问题迁移:如图2,AB∥ED,求∠B+∠BCD+∠D的度数.
(3)方法运用:如图3,AB∥CD,点C在D的右侧,∠ADC=70°,点B在A的左侧,∠ABC=60°,BE平分∠ABC,DE平分∠ADC,BE、DE所在的直线交于点E,点E在AB与CD两条平行线之间,求∠BED的度数.
参考答案
一.选择题(共10小题)
1.【解答】解:根据对顶角的意义得,D选项的图象符合题意,
故选:D.
2.【解答】解:根据题意可得:3条直线相交于一点时交点最少,此时交点为1个,即m=1;
任意两直线相交都产生一个交点时交点最多,3条直线相交,交点最多为3个,即n=3;
则m+n=1+3=4.
故选:A.
3.【解答】解:①画出线段AB的中点,线段表示错误;
②A,B两点的距离只能测量,此语句错误;
③射线不能顺向延长,只能反向延长,此语句错误;
④连接A,B两点,此语句正确;
故选:A.
4.【解答】解:A、∠AOD=∠BOC,说法正确;
B、∠AOC=∠AOE,说法错误;
C、∠AOE+∠BOD=90°,说法正确;
D、∠AOD+∠BOD=180°,说法正确;
故选:B.
5.【解答】解:A、∠C=∠ABE不能判断出EB∥AC,故本选项错误;
B、∠BAC=∠EBD不能判断出EB∥AC,故本选项错误;
C、∠ABC=∠BAE只能判断出EA∥CD,不能判断出EB∥AC,故本选项错误;
D、∠BAC=∠ABE,根据内错角相等,两直线平行,可以得出EB∥AC,故本选项正确.
故选:D.
6.【解答】解:∵直线m∥n,
∴∠3=∠2=34°.
∵∠1+∠BAC+∠3=180°,∠1=63°,∠3=34°,
∴∠BAC=180°﹣63°﹣34°=83°.
故选:B.
7.【解答】解:根据题意,∠A′=∠A=90°,∠ABE=∠A′BE,
∵∠CBA′=30°,
∴∠BEA′=180°﹣90°﹣30°=60°,
故选:D.
8.【解答】解:∵AB∥EF,AB∥CD,
∴EF∥CD,
∴∠3=∠CGE,
∴∠3﹣∠1=∠CGE﹣∠1=∠BGE,
∵AB∥EG,
∴∠2+∠BGE=180°,
即∠2+∠3﹣∠1=180°,
故选:A.
9.【解答】解:如图,当∠1=∠2=∠3时,
∵∠1=∠2,
∴a∥c,
∵a∥b,
∴c∥b,
∴∠3=∠4,
∵∠1=∠2=∠3,
∴∠1=∠2=∠3=∠4,
∴∠2=(∠1+∠4)=[(3m+10)°+(7m﹣30)°]=(5m﹣10)°,
故选项D正确,
故选:D.
10.【解答】解:(1)∵∠3=∠4,∴BD∥AC;
(2)∵∠1=∠2,∴AB∥CD;
(3)∵∠A=∠DCE,∴AB∥CD;
(4)∵∠D+∠ABD=180°,∴AB∥CD,
故选:C.
二.填空题(共8小题)
11.【解答】解:根据“垂线段最短”可知,PB最短,
故答案为:PB.
12.【解答】解:只用没有刻度的直尺和圆规进行的作图称为尺规作图.
故答案为:没有刻度的,圆规.
13.【解答】解:根据对顶角相等,得零件的锥角等于30°,
∴∠1=180°﹣30°=150°.
故答案为:150.
14.【解答】解:∵∠1=80°,
∴∠3=80°.
∵a∥b,
∴∠2+∠3=180°,
∴∠2=180°﹣80°=100°.
故答案为:100°.
15.【解答】解:由图形得,有两个相等的同位角存在,
这样做的依据是:同位角相等,两直线平行.
故答案为:同位角相等,两直线平行.
16.【解答】解:∵CD∥EF,
∴∠2+∠CEF=180°,
∵AB∥EF,
∴∠1=∠3+∠CEF,
∴∠CEF=∠1﹣∠3,
∴∠2+∠1﹣∠3=180°,
即∠1﹣∠3+∠2=180°.
故答案为:∠1﹣∠3+∠2=180°.
17.【解答】解:如图1,∠EOD在∠BOD外面,
∵∠AOC=50°,
∴∠BOD=50°,
∴∠BOE=∠BOD+∠EOD=70°;
如图2,∠EOD在∠BOD里面,
∵∠AOC=50°,
∴∠BOD=50°,
∴∠BOE=∠BOD﹣∠EOD=30°.
故∠BOE=70°或30°.
故答案为:70°或30°.
18.【解答】解:∵∠EBA=α°,∠EBA+∠EBD=180°,
∴∠EBD=180°﹣α°,
∵BF平分∠EBD,
∴∠FBD=∠EBD=(180°﹣α°)=90°﹣α°,
∵CG∥BF,
∴∠FBD=∠GCD,
∴∠GCD=90°﹣α°=(90﹣α)°,
故答案为:(90﹣α).
三.解答题(共7小题)
19.【解答】解:如图所示:
∵AD∥BC,
∴∠A+∠ABC=180°,∠ADB=∠CBD,
又∵∠A=110°,
∴∠ABC=180°﹣110°=70°,
又∵BE平分∠ABC,
∴∠CBD=
∴∠CBD=×70°=35°
∴∠ADB=35°.
20.【解答】解:设∠1=x°,那么∠2=2∠1=2x°,∠3=3∠2=6x°;
∵∠2=∠FOD,∠1+∠FOD+∠3=180°,
∴x+2x+6x=180,
解得,x=20,
即:∠1=20°,∠2=40°,∠3=120°,
21.【解答】证明:∵∠1=55°(已知),
∴∠CNM=55°(对顶角相等),
∵∠2=125°(已知),
∴∠CNM+∠2=180°(等式的性质),
∴AB∥CD(同旁内角互补,两直线平行).
22.【解答】解:(1)①如图所示:
②如图所示:
(2)①线段 AD的长度是点A到BC的距离,线段AF的长度是点 F到直线 AB的距离;
②在线段AB、AD、AF、AC中,长度最短的是线段 AD,理由是:直线外一点与直线上各点连接的所有线段中,垂线段最短;
③∵CE∥AB,
∴∠BCE=∠B,∠BAG=∠ACE.
∵∠ACE=∠BCE+∠ACB.
∴∠BAG=∠B+∠ACB.
故答案为:AD,F,AB;AD,垂线段.
23.【解答】解:(1)∵∠AOE+∠AOF=180°,∠AOE=40°,
∴∠AOF=180°﹣∠AOE=140°
∵OC平分∠AOF,
∴∠AOC=∠AOF=×140°=70°
∵∠AOB=90°
∴∠BOD=180°﹣∠AOC﹣∠AOB=180°﹣70°﹣90°=20°
(2)方法同(1)可得,若∠AOE=30°,则∠BOD=15°
(3)猜想:∠BOD=∠AOE,
理由如下:
∵OC平分∠AOF
∴∠AOC=∠AOF
∵∠AOE+∠AOF=180°,
∴∠AOF=180°﹣∠AOE
∵∠BOD+∠AOB+∠AOC=180°,∠AOB=90°
∴∠BOD+90°+∠AOF=180°,
∴∠BOD=90°﹣∠AOF=90°﹣90°+∠AOE=∠AOE.
24.【解答】解:(1)①∵AM∥BN,∠A=64°,
∴∠ABN=180°﹣∠A=116°,
故答案为:116°;
②∵AM∥BN,
∴∠ACB=∠CBN,
故答案为:CBN;
(2)∵AM∥BN,
∴∠ABN+∠A=180°,
∴∠ABN=180°﹣64°=116°,
∴∠ABP+∠PBN=116°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=116°,
∴∠CBD=∠CBP+∠DBP=58°;
(3)不变,
∠APB:∠ADB=2:1,
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB:∠ADB=2:1;
(4)∵AM∥BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,
则有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN
∴∠ABC=∠DBN,
由(1)∠ABN=116°,
∴∠CBD=58°,
∴∠ABC+∠DBN=58°,
∴∠ABC=29°,
故答案为:29°.
25.【解答】解::(1)∵ED∥BC,
∴∠B=∠EAB,∠C=∠DAC,
(2)∵AB∥DE,
∴CF∥DE,
∴∠D=∠FCD,
∵CF∥AB,
∴∠B=∠BCF,
∵∠BCF+∠BCD+∠DCF=360°,
∴∠B+∠BCD+∠D=360°,
(3)如图3,过点E作EF∥AB,
∵AB∥CD,∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=60°,∠ADC=70°,
∴∠ABE=∠ABC=30°,∠CDE=∠ADC=35°
∴∠BED=∠BEF+∠DEF=30°+35°=65°.
故答案为:∠EAB,∠DAC.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
