六年级下册数学课件-比例 青岛版(共17张PPT)
文档属性
| 名称 | 六年级下册数学课件-比例 青岛版(共17张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 489.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 07:20:39 | ||
图片预览






文档简介
课件17张PPT。比例的意义和基本性质巩固练习1、两个数( ),又叫作两个数的比,
比的( )除以( )所得到的商叫作( )。
2、比的基本性质:( )。一、课前复习:3、求出下列各比的比值,哪些比值相等?
80:4 16:2 40:80 20:10
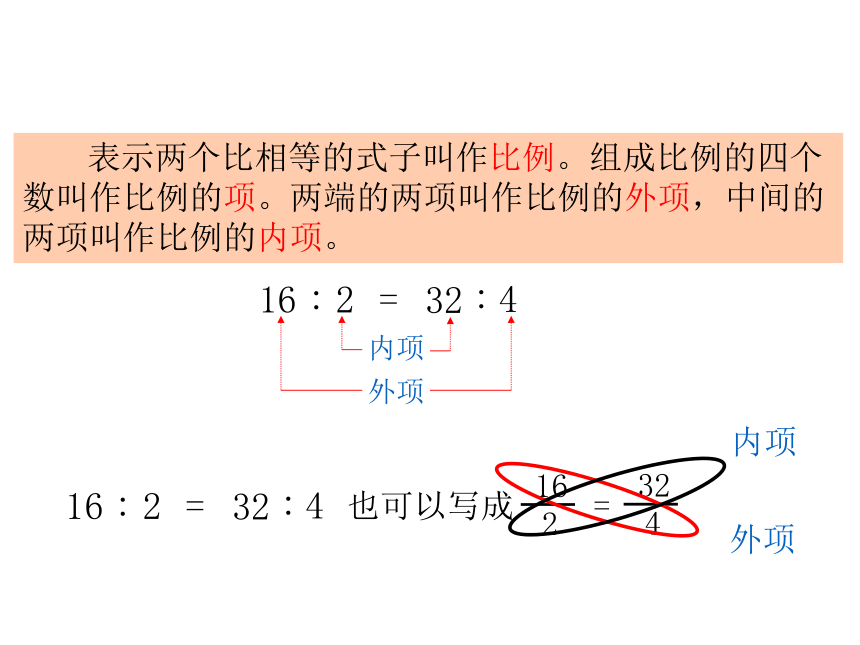
0.4:0.8 : 0.8:0.04 32:4 表示两个比相等的式子叫作比例。组成比例的四个数叫作比例的项。两端的两项叫作比例的外项,中间的两项叫作比例的内项。内项外项也可以写成162324=内项外项运动会报名 男生志愿者
王东 李明 刘刚
李亮 丁一 张帅
于军 刘平 赵海女生志愿者
李燕 王静 牛莉
方悦 于美 张红
孙娟 第一天运了2次共运16吨共运32吨问题一:这两天运输量和运输次数的比各是多少?
问题二:在这个比例里,两个外项与两个内项之间有什么关系呢?第二天运了4次运输量和运输次数的比各是多少?小组合作,猜想规律 分别算出两个外项和两个内项的和、差、积、商,看看从中能发现什么规律? 可以先借助“16:2=32:4”为例来研究。在这个比例里,两个外项与两个内项之间有什么关系呢?=16:232:4合作探索两个外项的和与两个内项的和:两个外项的和:16 + 4 = 20 两个内项的和:2 + 32 = 34 两个外项的和与两个内项的和之间没有发现规律。1 6 : 2 = 32: 4 两个外项的差与两个内项的差:两个外项的差:16 - 4 = 12 两个内项的差:32- 2 = 30 1 6 : 2 = 32 : 4 两个外项的差与两个内项的差之间没有发现规律。合作探索两个外项的积与两个内项的积:两个外项的积:16 × 4 = 64 两个内项的和:2 × 32 = 64 1 6 : 2 = 32 : 4 两个外项的积等于两个内项的积。合作探索两个外项的商与两个内项的商:两个外项的商:16 ÷ 4 = 4 两个内项的商:32÷ 2 = 16 1 6 : 2 = 32 : 4 两个外项的商与两个内项的商之间没有发现规律。合作探索合作探索回顾刚才的研究,可以得出一个什么结论?在比例里,两个外项的积等于两个内项的积。验证规律、总结规律两个内项的积:4 ×100 = 400 两个外项的积:80 × 5 = 400 = 40 : 2 = 60 : 3两个内项的积:2 × 60 = 120 两个外项的积:40 × 3 = 120 举例验证:10 : 7 = 20 :14 两个内项的积:7 × 20 = 140 两个外项的积:10 ×14 = 140 … 在比例里,两个外项的积等于两个内项的积。这叫作比例的基本性质。巩固拓展,应用规律
利用比例的基本性质,可以解决许多数学问题
2:1=4:( ) 1.4:2=( ):3
= : =3:( )知识点三:你能求出下面比例中的未知项吗?20 : 25 = 4 : χ解: 20χ= 25 × 4 20χ= 100χ= 5
求比例中的未知项,叫作解比例。
巩固练习:解:4χ=6.5×6
4χ÷4=39÷4
χ =9.75解:8χ=5×16
8χ÷8=80 ÷8
χ =10解: 0.3χ=1.5×4.2
0.3χ÷0.3=6.3÷3
χ =2.1表示两个比相等的式子叫做比例。组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。在比例里,两个外项的积等于两个内项的积,叫做比例的基本性质。
利用比例的性质解比例。(交叉相乘)三、畅谈收获比例的意义和基本性质六、达标检测1、解比例2、在一个比例中,两个内项的积是10。一个外项是4,另一个外项是多少?六、达标检测(答案)1、解比例2、在一个比例中,两个内项的积是10。一个外项是4,另一个外项是多少? χ=1545 χ= χ=28 10÷4=2.5 答:另一个外项是2.5
比的( )除以( )所得到的商叫作( )。
2、比的基本性质:( )。一、课前复习:3、求出下列各比的比值,哪些比值相等?
80:4 16:2 40:80 20:10
0.4:0.8 : 0.8:0.04 32:4 表示两个比相等的式子叫作比例。组成比例的四个数叫作比例的项。两端的两项叫作比例的外项,中间的两项叫作比例的内项。内项外项也可以写成162324=内项外项运动会报名 男生志愿者
王东 李明 刘刚
李亮 丁一 张帅
于军 刘平 赵海女生志愿者
李燕 王静 牛莉
方悦 于美 张红
孙娟 第一天运了2次共运16吨共运32吨问题一:这两天运输量和运输次数的比各是多少?
问题二:在这个比例里,两个外项与两个内项之间有什么关系呢?第二天运了4次运输量和运输次数的比各是多少?小组合作,猜想规律 分别算出两个外项和两个内项的和、差、积、商,看看从中能发现什么规律? 可以先借助“16:2=32:4”为例来研究。在这个比例里,两个外项与两个内项之间有什么关系呢?=16:232:4合作探索两个外项的和与两个内项的和:两个外项的和:16 + 4 = 20 两个内项的和:2 + 32 = 34 两个外项的和与两个内项的和之间没有发现规律。1 6 : 2 = 32: 4 两个外项的差与两个内项的差:两个外项的差:16 - 4 = 12 两个内项的差:32- 2 = 30 1 6 : 2 = 32 : 4 两个外项的差与两个内项的差之间没有发现规律。合作探索两个外项的积与两个内项的积:两个外项的积:16 × 4 = 64 两个内项的和:2 × 32 = 64 1 6 : 2 = 32 : 4 两个外项的积等于两个内项的积。合作探索两个外项的商与两个内项的商:两个外项的商:16 ÷ 4 = 4 两个内项的商:32÷ 2 = 16 1 6 : 2 = 32 : 4 两个外项的商与两个内项的商之间没有发现规律。合作探索合作探索回顾刚才的研究,可以得出一个什么结论?在比例里,两个外项的积等于两个内项的积。验证规律、总结规律两个内项的积:4 ×100 = 400 两个外项的积:80 × 5 = 400 = 40 : 2 = 60 : 3两个内项的积:2 × 60 = 120 两个外项的积:40 × 3 = 120 举例验证:10 : 7 = 20 :14 两个内项的积:7 × 20 = 140 两个外项的积:10 ×14 = 140 … 在比例里,两个外项的积等于两个内项的积。这叫作比例的基本性质。巩固拓展,应用规律
利用比例的基本性质,可以解决许多数学问题
2:1=4:( ) 1.4:2=( ):3
= : =3:( )知识点三:你能求出下面比例中的未知项吗?20 : 25 = 4 : χ解: 20χ= 25 × 4 20χ= 100χ= 5
求比例中的未知项,叫作解比例。
巩固练习:解:4χ=6.5×6
4χ÷4=39÷4
χ =9.75解:8χ=5×16
8χ÷8=80 ÷8
χ =10解: 0.3χ=1.5×4.2
0.3χ÷0.3=6.3÷3
χ =2.1表示两个比相等的式子叫做比例。组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。在比例里,两个外项的积等于两个内项的积,叫做比例的基本性质。
利用比例的性质解比例。(交叉相乘)三、畅谈收获比例的意义和基本性质六、达标检测1、解比例2、在一个比例中,两个内项的积是10。一个外项是4,另一个外项是多少?六、达标检测(答案)1、解比例2、在一个比例中,两个内项的积是10。一个外项是4,另一个外项是多少? χ=1545 χ= χ=28 10÷4=2.5 答:另一个外项是2.5
