高中数学人教新课标A版选修4-5第一讲 不等式和绝对值不等式一 不等式(共43张PPT)
文档属性
| 名称 | 高中数学人教新课标A版选修4-5第一讲 不等式和绝对值不等式一 不等式(共43张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 11:09:53 | ||
图片预览










文档简介
(共43张PPT)
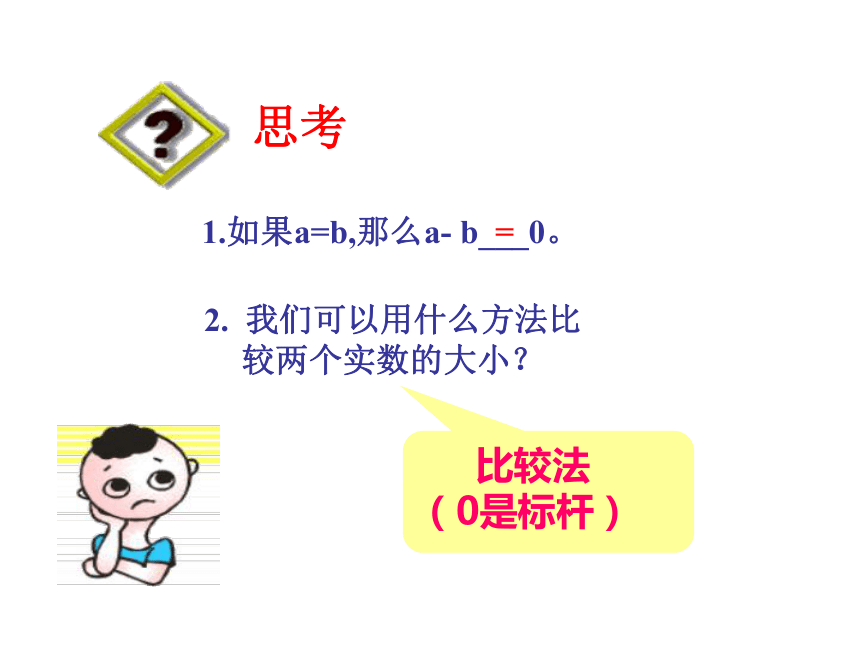
回顾旧知
a___b
______>0
a___b
______<0
>
a-b
<
a-b
1.如果a=b,那么a- b___0。
2. 我们可以用什么方法比较两个实数的大小?
=
比较法
(0是标杆)
通过考察它们与0的大小关系,得出结论。
比较(x+1)(x+2)与(x-3)(x+6)得大小。
解:因为
> 0
所以
(x+1)(x+2)-(x-3)(x+6)
=(x2+3x+2)-(x2+3x-18)
=20
(x+1)(x+2)>(x-3)(x+6)
等式有“等式两边同加(或减)一个数,等式仍然成立”“等式两边同乘(或除以)一个数,等式仍然成立”等基本性质。类比等式的这些性质,不等式有哪些基本性呢?
(5) a>b>0
(6) a>b>0
an>bn
观察不等式的基本性质,并与不等式的基本性质比较,你认为在研究不等式时,需要特别注意什么问题?
特别注意“符号问题”
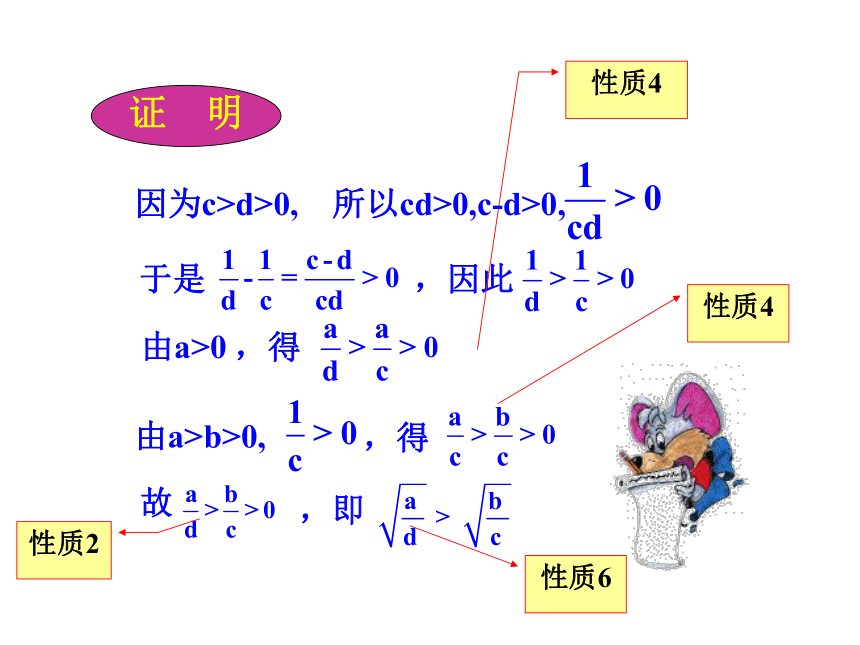
性质4
性质4
性质2
性质6
因为a2+b2-2ab=(a-b)2≥0,当且仅当a=b时等号成立,所以a2+b2≥2ab,当且仅当a=b时,等号成立。
你能从几何的角度解释上述定理吗?
即矩形BCGH和矩形JCDI成为两个正方形时等号成立。
如图,S正方形ABCD+S正方形CEFG=a2+b2, S矩形BCGH+S锯形JCDI=2ab.
有图形可知,a2+b2≥2ab,当且仅当a=b时,等号成立。
重要不等式
基本不等式
观察下图,如果AD=a,BD=b,OC是斜边AB的中线,你能给出基本不等式的几何意义吗?
分 析
所以∠DCA= ∠B.
于是Rt△DCA和Rt△DBC相似.
综上所述可知,基本不等式的几何意义是:直角三角形斜边上的中线不小于斜边上的高。(即半弦长小于等于半径)
求证:
(1)在所有周长相同的矩形中,正方形的面积最大;
(2)在所有面积相同的矩形中,正方形的周长最短。
基本不等式涉及两个正数的和与积之间的数量关系,所以可以考虑利用基本不等式进行证明。
设矩形的长为x,宽为y。
(1)设矩形周长为定值L,即2x+2y=L。
(2)设矩形面积为定值S,即xy=S为定值。
基本
不等式
对两个正实数x,y,如果它们的和S是定值,则当且仅当x=y时,它们的积P取得最大值;如果它们的积P是定值,则当且仅当x=y时,它们的和S取得最小值。
很重要!
简称:一 “正”, 二“定”,
三“相等”
某居民小区要建
一座八边形的休闲场所,
它的主体造型平面图(如图)
是由两个相同的矩形ABCD和
EFGH构成的面积为200平方米
的十字型地域.计划在正方形MNPQ上建一座花坛,造价为每平方米4200元,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角(图中四个三角形)上铺草坪,造价为每平方米80元。
(1)设总造价为S元,AD长为x米,试建立S关于x的函数关系式;
(2)当x为何值时,S最小?并求出这个最小值。
该问题属于利用基本不等式解决最值问题。
求:
解:
(1)
(2)
由上可知,当AD约为3.16米时,休闲场所总造价S取最小值118000元。
根据基本不等式得
所以S ≥38000+80000=118000,
反 思
利用基本不等式解决极值问题,要先写出函数的解析式,然后判断是否可以借助于基本不等式去解决。
基本不等式给出了两个正数的算术平均数与几何平均数的关系,这个不等式能否推广呢?例如,对于3个正数,会有怎样的不等式成立?
(x+y)3=x3+3x2y+3xy2+y3
x3+y3=(x+y)(x2-xy+y2)
由于a3+b3+c3-3abc
=(a+b)3-3a2b-3ab2+c3-3abc
=(a+b)3+c3-3a2-3ab2-3abc
=(a+b+c)〔 (a+b)2-(a+b)c+c2 〕-3ab(a+b+c)
=(a+b+c)(a2+b2+c2-ab-bc-ca)
=(a+b+c) 〔 (a-b)2-(b-c)2+(c-a)2 〕≥0
所以a3+b3+c3 ≥3abc,当且仅当a=b=c时,
等号成立。
三个正数的算术平均数不小于它们的几何平均数
本题涉及三个实数的和积,可以考虑基本不等式的推广。
在表面积一定的长方体中,以正方体的体积最大吗?
设长方体的三条相交于同一顶点的棱的长分别为x,y,z,则长方体的体积为V=xyz,
即x=y=z时,等号成立。
所以,当长方体是正方体时,体积取得最大值,最大值是
1.不等式的基本性质。
2. 基本不等式及其应用。
3.基本不等式的推广
2.若M=(2x+3)(x-4),N=(x-7)(x+3)+8,讨论M与N的大小关系。
习题1.1(第9页)
1.(1)假命题 (2)假命题
(3)假命题 (4)真命题
回顾旧知
a___b
______>0
a___b
______<0
>
a-b
<
a-b
1.如果a=b,那么a- b___0。
2. 我们可以用什么方法比较两个实数的大小?
=
比较法
(0是标杆)
通过考察它们与0的大小关系,得出结论。
比较(x+1)(x+2)与(x-3)(x+6)得大小。
解:因为
> 0
所以
(x+1)(x+2)-(x-3)(x+6)
=(x2+3x+2)-(x2+3x-18)
=20
(x+1)(x+2)>(x-3)(x+6)
等式有“等式两边同加(或减)一个数,等式仍然成立”“等式两边同乘(或除以)一个数,等式仍然成立”等基本性质。类比等式的这些性质,不等式有哪些基本性呢?
(5) a>b>0
(6) a>b>0
an>bn
观察不等式的基本性质,并与不等式的基本性质比较,你认为在研究不等式时,需要特别注意什么问题?
特别注意“符号问题”
性质4
性质4
性质2
性质6
因为a2+b2-2ab=(a-b)2≥0,当且仅当a=b时等号成立,所以a2+b2≥2ab,当且仅当a=b时,等号成立。
你能从几何的角度解释上述定理吗?
即矩形BCGH和矩形JCDI成为两个正方形时等号成立。
如图,S正方形ABCD+S正方形CEFG=a2+b2, S矩形BCGH+S锯形JCDI=2ab.
有图形可知,a2+b2≥2ab,当且仅当a=b时,等号成立。
重要不等式
基本不等式
观察下图,如果AD=a,BD=b,OC是斜边AB的中线,你能给出基本不等式的几何意义吗?
分 析
所以∠DCA= ∠B.
于是Rt△DCA和Rt△DBC相似.
综上所述可知,基本不等式的几何意义是:直角三角形斜边上的中线不小于斜边上的高。(即半弦长小于等于半径)
求证:
(1)在所有周长相同的矩形中,正方形的面积最大;
(2)在所有面积相同的矩形中,正方形的周长最短。
基本不等式涉及两个正数的和与积之间的数量关系,所以可以考虑利用基本不等式进行证明。
设矩形的长为x,宽为y。
(1)设矩形周长为定值L,即2x+2y=L。
(2)设矩形面积为定值S,即xy=S为定值。
基本
不等式
对两个正实数x,y,如果它们的和S是定值,则当且仅当x=y时,它们的积P取得最大值;如果它们的积P是定值,则当且仅当x=y时,它们的和S取得最小值。
很重要!
简称:一 “正”, 二“定”,
三“相等”
某居民小区要建
一座八边形的休闲场所,
它的主体造型平面图(如图)
是由两个相同的矩形ABCD和
EFGH构成的面积为200平方米
的十字型地域.计划在正方形MNPQ上建一座花坛,造价为每平方米4200元,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角(图中四个三角形)上铺草坪,造价为每平方米80元。
(1)设总造价为S元,AD长为x米,试建立S关于x的函数关系式;
(2)当x为何值时,S最小?并求出这个最小值。
该问题属于利用基本不等式解决最值问题。
求:
解:
(1)
(2)
由上可知,当AD约为3.16米时,休闲场所总造价S取最小值118000元。
根据基本不等式得
所以S ≥38000+80000=118000,
反 思
利用基本不等式解决极值问题,要先写出函数的解析式,然后判断是否可以借助于基本不等式去解决。
基本不等式给出了两个正数的算术平均数与几何平均数的关系,这个不等式能否推广呢?例如,对于3个正数,会有怎样的不等式成立?
(x+y)3=x3+3x2y+3xy2+y3
x3+y3=(x+y)(x2-xy+y2)
由于a3+b3+c3-3abc
=(a+b)3-3a2b-3ab2+c3-3abc
=(a+b)3+c3-3a2-3ab2-3abc
=(a+b+c)〔 (a+b)2-(a+b)c+c2 〕-3ab(a+b+c)
=(a+b+c)(a2+b2+c2-ab-bc-ca)
=(a+b+c) 〔 (a-b)2-(b-c)2+(c-a)2 〕≥0
所以a3+b3+c3 ≥3abc,当且仅当a=b=c时,
等号成立。
三个正数的算术平均数不小于它们的几何平均数
本题涉及三个实数的和积,可以考虑基本不等式的推广。
在表面积一定的长方体中,以正方体的体积最大吗?
设长方体的三条相交于同一顶点的棱的长分别为x,y,z,则长方体的体积为V=xyz,
即x=y=z时,等号成立。
所以,当长方体是正方体时,体积取得最大值,最大值是
1.不等式的基本性质。
2. 基本不等式及其应用。
3.基本不等式的推广
2.若M=(2x+3)(x-4),N=(x-7)(x+3)+8,讨论M与N的大小关系。
习题1.1(第9页)
1.(1)假命题 (2)假命题
(3)假命题 (4)真命题
