高中数学人教新课标A版选修4-5第一讲 不等式和绝对值不等式二 绝对值不等式(共35张PPT)
文档属性
| 名称 | 高中数学人教新课标A版选修4-5第一讲 不等式和绝对值不等式二 绝对值不等式(共35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 00:00:00 | ||
图片预览










文档简介
(共35张PPT)
回顾旧知
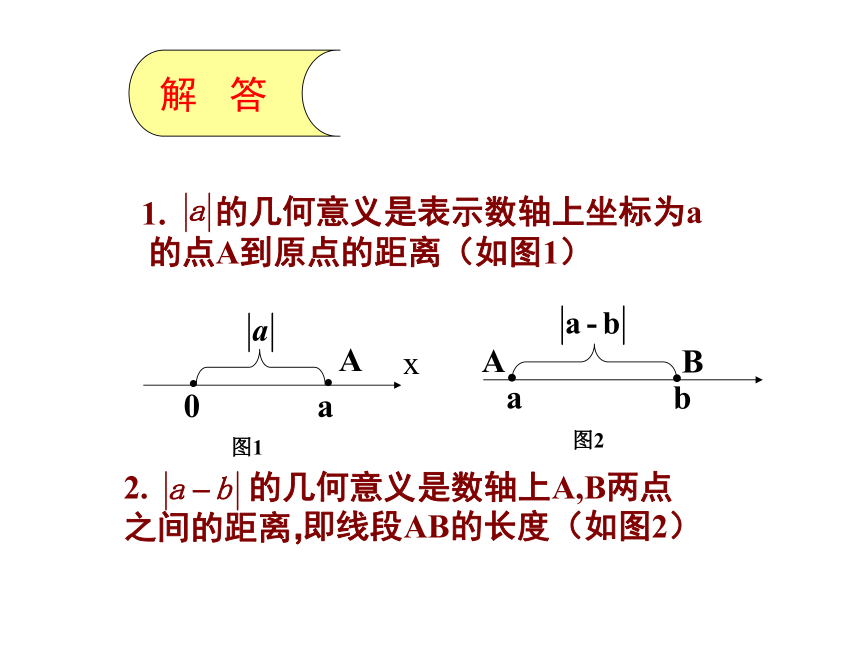
1.实数的a绝对值的几何意义是什么?
x
从“运算”的角度考察
分ab>0和ab<0情况讨论
(2)当ab<0时,又可以分a>0,b<0和a<0,b>0两中情况.
如果a>0,b>0时,如图2-1,
定理1
(很重要)
如果把定理1中的实数a,b分别换为向量a,b能得出什么结果?你能解释它的几何意义吗?
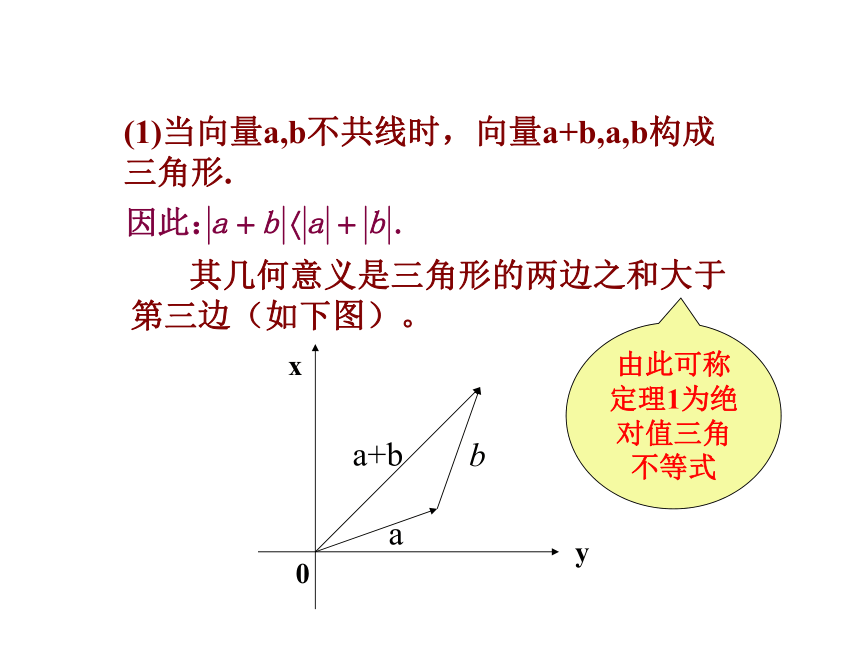
其几何意义是三角形的两边之和大于第三边(如下图)。
由此可称定理1为绝对值三角不等式
(1)当向量a,b不共线时,向量a+b,a,b构成三角形.
(2)当向量a,b共线时,分以下两种情况:
分类讨论
(1)当ab≥0时,
放缩法
利用定理1证明。
定理2
如果a,b,c是实数,那么│a-c│≤ │a-b│+ │b-c│ 当且仅当(a-b)(b-c)≥0时,等号成立.
其几何意义通过数轴考虑。
点B在点A,C之间
点B不在A,C之间
根据定理1,
当且仅当(a-b)(b-c)≥0时,等号成立.
两个施工队分别被安排在公路沿线的两个地点施工,这两个地点分别位于公路路碑的第10km和第20km处。现要在公路沿线建两个施工队的共同临时生活区,每个施工队每天在生活区和施工区地点之间往返一次。要使两个施工队每天往返的路程之和最小,生活区应该建在何处?
解不等式│2x-1│≤3
该题解的几何解释是什么?
如何求解│x-a│+│x-b│≥c和
│x-a│+│x-b│ ≤c型不等式?
思路一:对几何意义作分析;
思路二:把含绝对值的不等式转化为不含绝对值的不等式;
思路三:从函数的观点处理。
解法一:
设数轴上与-2,1对应的点分别是A,B。(如图)
所以,原不等式的解集是(-∞, -3] ∪[2, + ∞)
从数轴上可以看到,点A1和B1之间的任何点到点A,B的距离之和都小于5;点A1的左边或点B1的右边的任何点到点A,B的距离之和都大于5.
解不等式:
│x-1│+│x+2│≥5
解法二:
当x ≤-2时,原不等式可以为-(x-1)-(x+2) ≥5
解得 x ≤-3.
当x ≥1 时,原不等式可以化为 (x-1)+(x+2) ≥ 5
综上所述,原不等式的解集是(-∞, -3] ∪[2, + ∞)
解法三:
将原不等式转化为│x-1│+│x+2│-5≥0
构造函数y= │x-1│+│x+2│-5
作出图像(右图)可知,当x∈(-∞, -3) ∪[2, + ∞),
有y ≥0
所以,原不等式的解集是(-∞, -3] ∪[2, + ∞)
本题介绍了三种解决这类问题的方法,其中体现的思想方法具有普遍意义。解法一体现了数形结合思想,解法二体现了分类讨论思想,解法三体现了函数与方程的思想。
1.绝对值三角函数的几何意义。
2.两类绝对值不等式的解法。
1.解不等式│x2-2x│<3
解法一:
由│x2-2x│<3得-3解得-1所以,不等式的解集是(-1,3)
解法二:
│x2-2x│<3 表示函数图像中在直线 y=-3 和直线 y=3 之间相应部分的自变量的集合.
即不等式的解集是(-1,3).
作函数y=x2-2x的图像.
解方程x2-2x=3得x1=-1,x2=3
2.求函数y=│x-4│+ │x-6│的最小值.
解: y=│x-4│+ │x-6│
= │x-4│+ │6-x│
≥ │(x-4)+(6-x)│=2
当且仅当(x-4)+(6-x) ≥0
即x ∈[4,6]时,函数y取最小值2.
回顾旧知
1.实数的a绝对值的几何意义是什么?
x
从“运算”的角度考察
分ab>0和ab<0情况讨论
(2)当ab<0时,又可以分a>0,b<0和a<0,b>0两中情况.
如果a>0,b>0时,如图2-1,
定理1
(很重要)
如果把定理1中的实数a,b分别换为向量a,b能得出什么结果?你能解释它的几何意义吗?
其几何意义是三角形的两边之和大于第三边(如下图)。
由此可称定理1为绝对值三角不等式
(1)当向量a,b不共线时,向量a+b,a,b构成三角形.
(2)当向量a,b共线时,分以下两种情况:
分类讨论
(1)当ab≥0时,
放缩法
利用定理1证明。
定理2
如果a,b,c是实数,那么│a-c│≤ │a-b│+ │b-c│ 当且仅当(a-b)(b-c)≥0时,等号成立.
其几何意义通过数轴考虑。
点B在点A,C之间
点B不在A,C之间
根据定理1,
当且仅当(a-b)(b-c)≥0时,等号成立.
两个施工队分别被安排在公路沿线的两个地点施工,这两个地点分别位于公路路碑的第10km和第20km处。现要在公路沿线建两个施工队的共同临时生活区,每个施工队每天在生活区和施工区地点之间往返一次。要使两个施工队每天往返的路程之和最小,生活区应该建在何处?
解不等式│2x-1│≤3
该题解的几何解释是什么?
如何求解│x-a│+│x-b│≥c和
│x-a│+│x-b│ ≤c型不等式?
思路一:对几何意义作分析;
思路二:把含绝对值的不等式转化为不含绝对值的不等式;
思路三:从函数的观点处理。
解法一:
设数轴上与-2,1对应的点分别是A,B。(如图)
所以,原不等式的解集是(-∞, -3] ∪[2, + ∞)
从数轴上可以看到,点A1和B1之间的任何点到点A,B的距离之和都小于5;点A1的左边或点B1的右边的任何点到点A,B的距离之和都大于5.
解不等式:
│x-1│+│x+2│≥5
解法二:
当x ≤-2时,原不等式可以为-(x-1)-(x+2) ≥5
解得 x ≤-3.
当x ≥1 时,原不等式可以化为 (x-1)+(x+2) ≥ 5
综上所述,原不等式的解集是(-∞, -3] ∪[2, + ∞)
解法三:
将原不等式转化为│x-1│+│x+2│-5≥0
构造函数y= │x-1│+│x+2│-5
作出图像(右图)可知,当x∈(-∞, -3) ∪[2, + ∞),
有y ≥0
所以,原不等式的解集是(-∞, -3] ∪[2, + ∞)
本题介绍了三种解决这类问题的方法,其中体现的思想方法具有普遍意义。解法一体现了数形结合思想,解法二体现了分类讨论思想,解法三体现了函数与方程的思想。
1.绝对值三角函数的几何意义。
2.两类绝对值不等式的解法。
1.解不等式│x2-2x│<3
解法一:
由│x2-2x│<3得-3
解法二:
│x2-2x│<3 表示函数图像中在直线 y=-3 和直线 y=3 之间相应部分的自变量的集合.
即不等式的解集是(-1,3).
作函数y=x2-2x的图像.
解方程x2-2x=3得x1=-1,x2=3
2.求函数y=│x-4│+ │x-6│的最小值.
解: y=│x-4│+ │x-6│
= │x-4│+ │6-x│
≥ │(x-4)+(6-x)│=2
当且仅当(x-4)+(6-x) ≥0
即x ∈[4,6]时,函数y取最小值2.
