人教版数学八年级下册17.1 勾股定理第1课时 课件(32张ppt)
文档属性
| 名称 | 人教版数学八年级下册17.1 勾股定理第1课时 课件(32张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 07:20:01 | ||
图片预览



文档简介
课件32张PPT。17.1 勾股定理第1课时人教版数学八年级下册1.经历探索勾股定理及验证勾股定理的过程,了解勾股定理的探究方法及其内在联系.
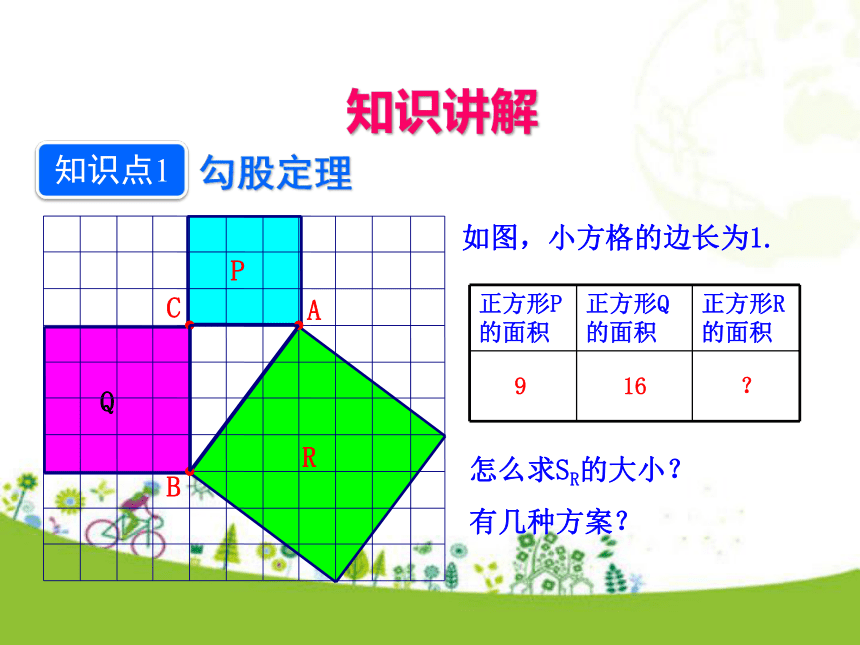
2.掌握勾股定理,并能运用勾股定理解决一些问题.学习目标这是1955年希腊为纪念一个数学学派发行的邮票.新课导入ABC916?怎么求SR的大小?
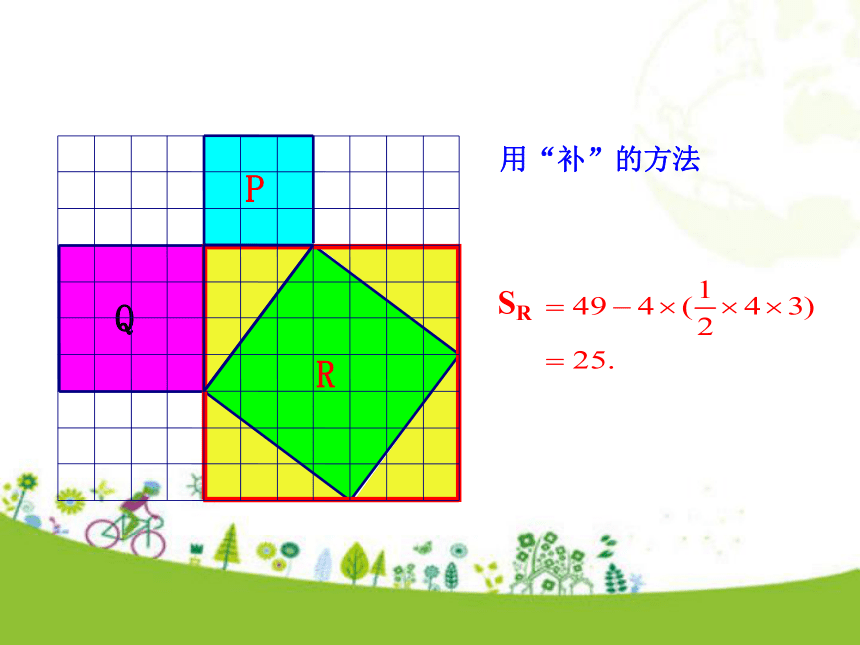
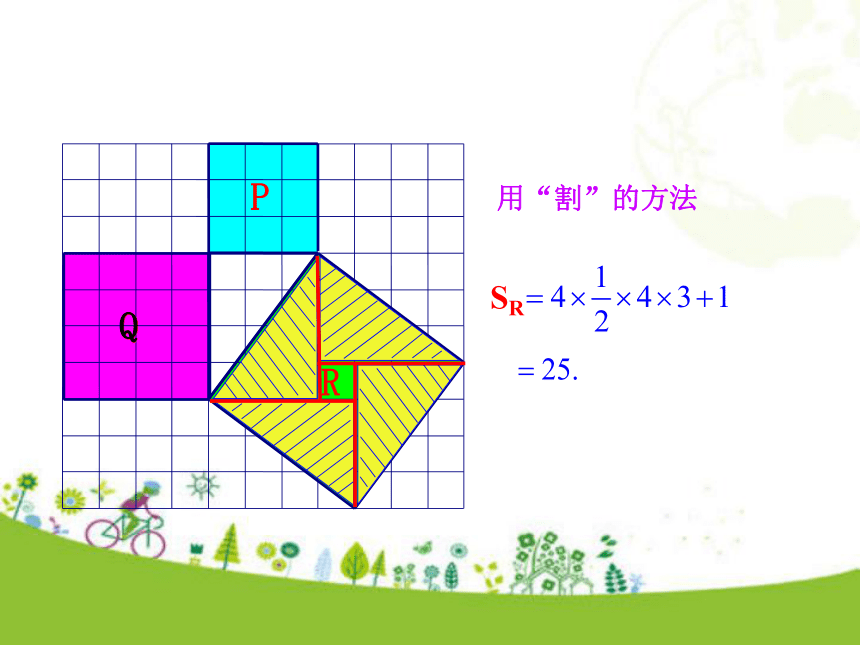
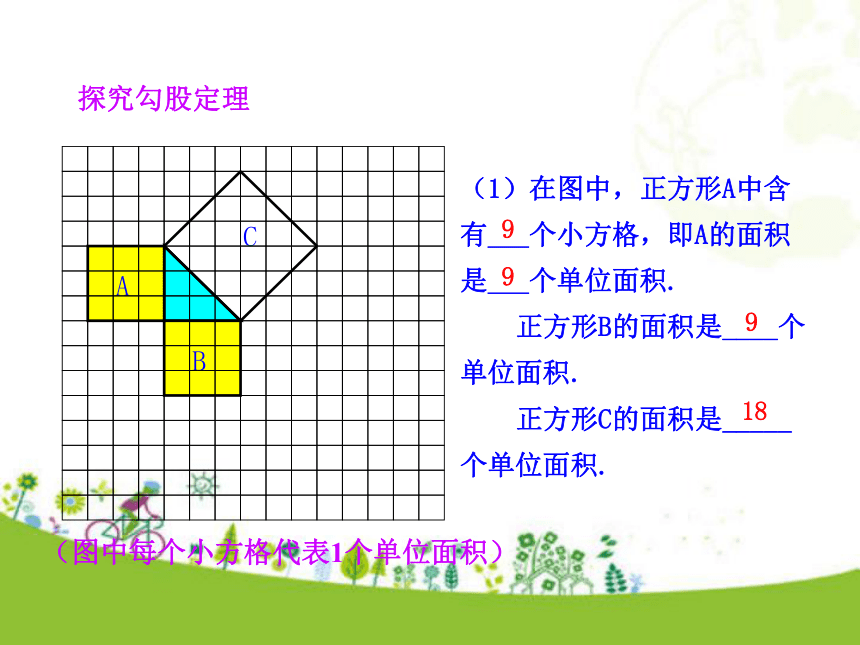
有几种方案?如图,小方格的边长为1.知识讲解勾股定理知识点1C用“补”的方法SR用“割”的方法QSR(图中每个小方格代表1个单位面积)(1)在图中,正方形A中含
有 个小方格,即A的面积
是 个单位面积.
正方形B的面积是____个
单位面积.
正方形C的面积是_____
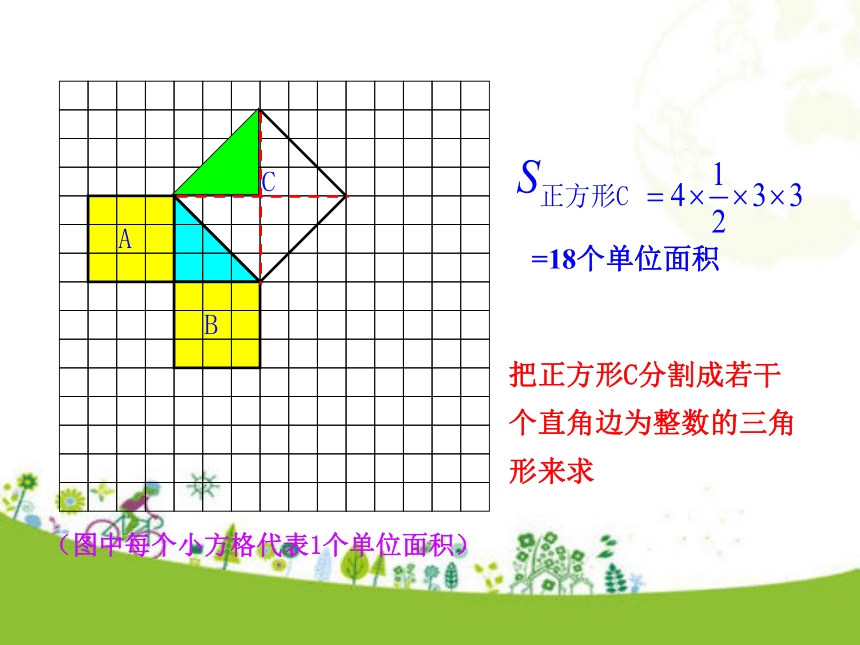
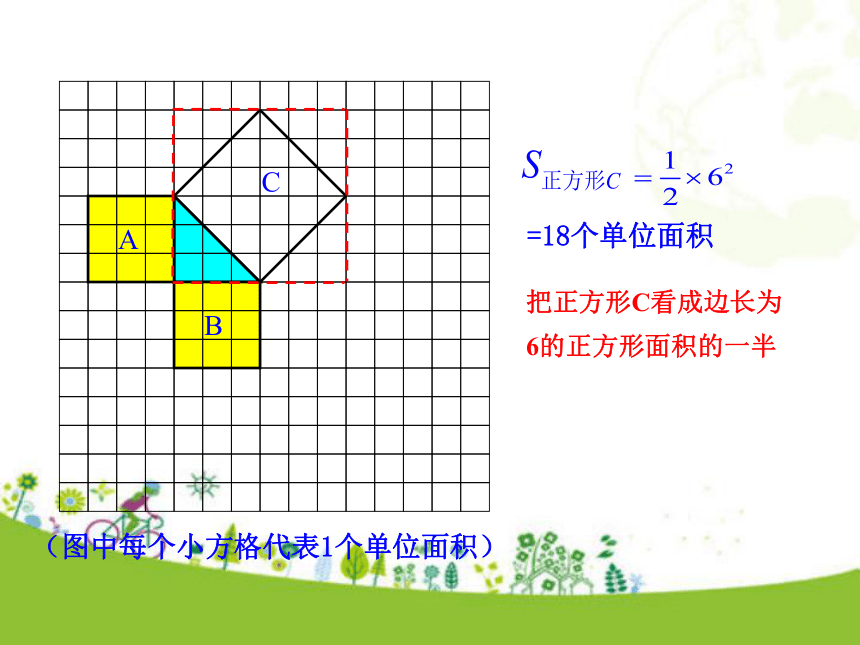
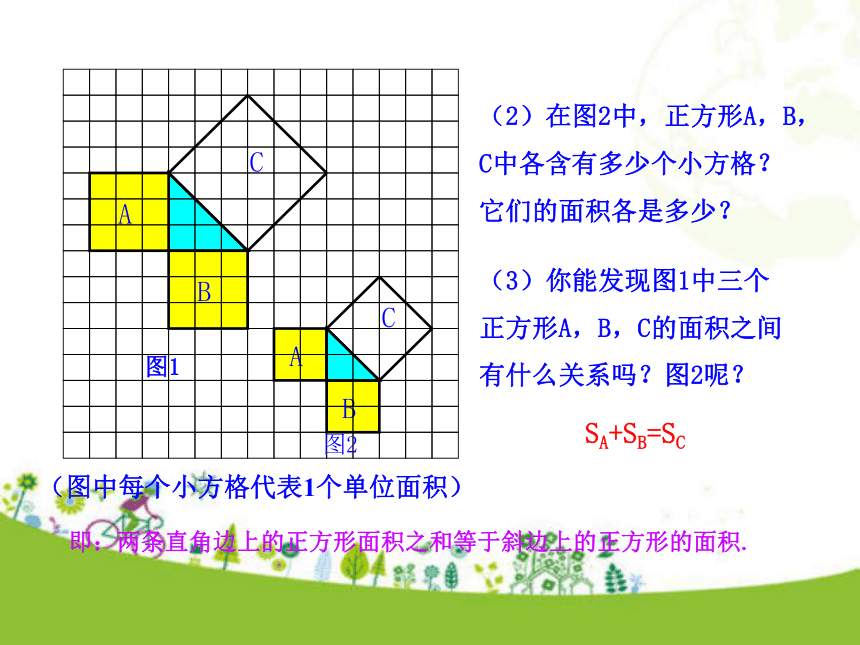
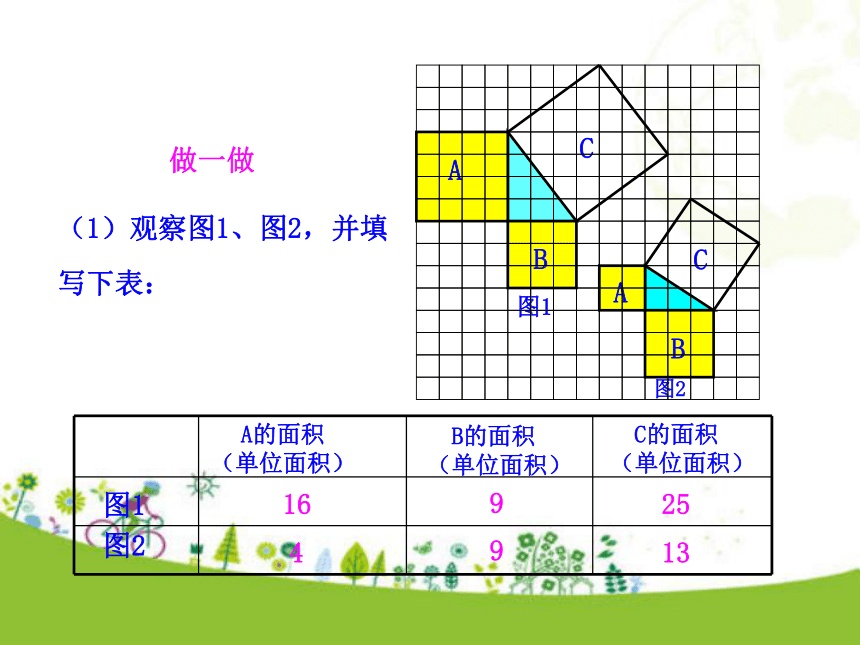
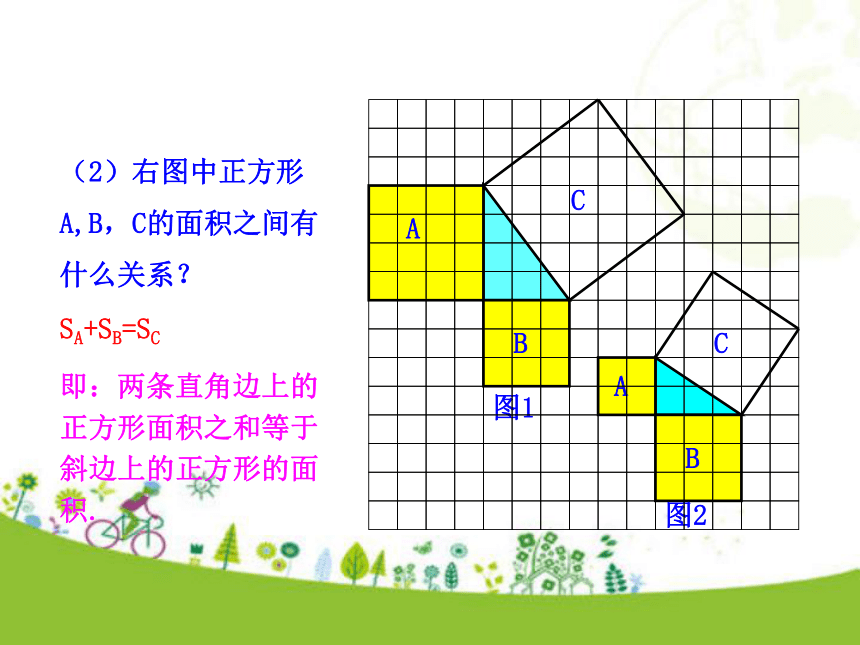
个单位面积.99918探究勾股定理 (图中每个小方格代表1个单位面积)把正方形C分割成若干个直角边为整数的三角形来求=18个单位面积(图中每个小方格代表1个单位面积)=18个单位面积把正方形C看成边长为6的正方形面积的一半(图中每个小方格代表1个单位面积)图1图2(2)在图2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?(3)你能发现图1中三个正方形A,B,C的面积之间有什么关系吗?图2呢?SA+SB=SC即:两条直角边上的正方形面积之和等于斜边上的正方形的面积.(1)观察图1、图2,并填写下表: A的面积(单位面积) B的面积(单位面积) C的面积(单位面积)图1图2169254913 做一做(2)右图中正方形A,B,C的面积之间有什么关系?SA+SB=SC即:两条直角边上的正方形面积之和等于斜边上的正方形的面积. 中国古代把直角三角形中较短的直角边叫做勾,较长的直角边叫做股,斜边叫做弦.
据《周髀算经》记载,西周战国时期(约公元前1千多年)有个叫商高的人对周公说,把一根直尺折成直角,两端连接得一个直角三角形,如果勾是3,股是4,那么弦等于5.345∟勾股弦人们还发现,在直角三角形中,勾是6,股是8,勾是5,股是12,弦一定是13, 是不是所有的直角三角形都有这个性质呢?世界上许多数学家,先后用不同方法证明了这个结论. 我国把它称为勾股定理.弦一定是10;勾股定理如果直角三角形两直角边分别为a,b,斜边为c,那么直角三角形两直角边的平方和等于
斜边的平方.勾股弦用两种方法表示大正方形的面积:对比两种表示方法,你得到勾股定理了吗?我们用另外一种方法来说明勾股定理是正确的1.设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a.b=8c=13a=20即学即练2.如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形A,B,C,D的边长分别是12,16,9,12,求最大正方形E的面积.解:根据图形正方形E 的边长为: 故E的面积为:252=625.勾股定理的证明知识点2命题
如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2. 如图我国古代证明该命题的“赵爽弦图”.赵爽指出:按弦图,又可以勾股相乘为朱实二,倍之为朱实四.以勾股之差自相乘为中黄实.加差实,亦成弦实.你是如何理解的?你会证明吗? 证明S=a2+b2acbacb小正方形的面积= (a-b)2即c2=a2+b2.原命题是正确的,又因为该命题与直角三角形的边有关,我国把它称为勾股定理。你理解了吗?原命题是否正确? 世界上几个文明古国相继发现和研究过勾股定理,据说其证明方法多达400 多种,有兴趣的同学可以继续研究.1.作 8 个全等的直角三角形(2 条直角边长分别为
a、b斜边长为 c)再作3个边长分别为 a、b、c 的正方形把它们拼成两个正方形(如图)你能利用这两个图形验证勾股定理吗? 写出你的验证过程.即学即练解:由图可知大正方形的边长为:a+b则面积为(a+b)2,图中把大正方形的面积分成了四部分,分别是:边长为a的正方形,边长为b的正方形,还有两个长为b,宽为a的长方形.
根据同一个图形面积相等,由左图可得
(a+b)2=a2+b2+4× ab,
由右图可得(a+b)2=c2+4× ab.
所以a2+b2=c2.1.在直角三角形中,满足条件的三边长可以是 .(写出一组即可)
【解析】答案不唯一,只要满足式子a2+b2=c2即可.
答案:3,4,5(满足题意的均可) 随堂练习 4.在Rt△ABC中,∠C=90°,a=6,c=10,则b= .5.求斜边长17 cm、一条直角边长15 cm的直角三角形的面积.【解析】设另一条直角边长是x cm.由勾股定理得:
152+ x2 =172,x2=172-152=289–225=64,
所以 x=±8(负值舍去),
所以另一直角边长为8 cm,直角三角形的面积是: (cm2).通过本课时的学习,需要我们掌握:
勾股定理:
直角三角形两直角边的平方和等于斜边的平方,即课堂小结谢谢!
2.掌握勾股定理,并能运用勾股定理解决一些问题.学习目标这是1955年希腊为纪念一个数学学派发行的邮票.新课导入ABC916?怎么求SR的大小?
有几种方案?如图,小方格的边长为1.知识讲解勾股定理知识点1C用“补”的方法SR用“割”的方法QSR(图中每个小方格代表1个单位面积)(1)在图中,正方形A中含
有 个小方格,即A的面积
是 个单位面积.
正方形B的面积是____个
单位面积.
正方形C的面积是_____
个单位面积.99918探究勾股定理 (图中每个小方格代表1个单位面积)把正方形C分割成若干个直角边为整数的三角形来求=18个单位面积(图中每个小方格代表1个单位面积)=18个单位面积把正方形C看成边长为6的正方形面积的一半(图中每个小方格代表1个单位面积)图1图2(2)在图2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?(3)你能发现图1中三个正方形A,B,C的面积之间有什么关系吗?图2呢?SA+SB=SC即:两条直角边上的正方形面积之和等于斜边上的正方形的面积.(1)观察图1、图2,并填写下表: A的面积(单位面积) B的面积(单位面积) C的面积(单位面积)图1图2169254913 做一做(2)右图中正方形A,B,C的面积之间有什么关系?SA+SB=SC即:两条直角边上的正方形面积之和等于斜边上的正方形的面积. 中国古代把直角三角形中较短的直角边叫做勾,较长的直角边叫做股,斜边叫做弦.
据《周髀算经》记载,西周战国时期(约公元前1千多年)有个叫商高的人对周公说,把一根直尺折成直角,两端连接得一个直角三角形,如果勾是3,股是4,那么弦等于5.345∟勾股弦人们还发现,在直角三角形中,勾是6,股是8,勾是5,股是12,弦一定是13, 是不是所有的直角三角形都有这个性质呢?世界上许多数学家,先后用不同方法证明了这个结论. 我国把它称为勾股定理.弦一定是10;勾股定理如果直角三角形两直角边分别为a,b,斜边为c,那么直角三角形两直角边的平方和等于
斜边的平方.勾股弦用两种方法表示大正方形的面积:对比两种表示方法,你得到勾股定理了吗?我们用另外一种方法来说明勾股定理是正确的1.设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a.b=8c=13a=20即学即练2.如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形A,B,C,D的边长分别是12,16,9,12,求最大正方形E的面积.解:根据图形正方形E 的边长为: 故E的面积为:252=625.勾股定理的证明知识点2命题
如果直角三角形两直角边长分别为a,b,斜边长为c,那么a2+b2=c2. 如图我国古代证明该命题的“赵爽弦图”.赵爽指出:按弦图,又可以勾股相乘为朱实二,倍之为朱实四.以勾股之差自相乘为中黄实.加差实,亦成弦实.你是如何理解的?你会证明吗? 证明S=a2+b2acbacb小正方形的面积= (a-b)2即c2=a2+b2.原命题是正确的,又因为该命题与直角三角形的边有关,我国把它称为勾股定理。你理解了吗?原命题是否正确? 世界上几个文明古国相继发现和研究过勾股定理,据说其证明方法多达400 多种,有兴趣的同学可以继续研究.1.作 8 个全等的直角三角形(2 条直角边长分别为
a、b斜边长为 c)再作3个边长分别为 a、b、c 的正方形把它们拼成两个正方形(如图)你能利用这两个图形验证勾股定理吗? 写出你的验证过程.即学即练解:由图可知大正方形的边长为:a+b则面积为(a+b)2,图中把大正方形的面积分成了四部分,分别是:边长为a的正方形,边长为b的正方形,还有两个长为b,宽为a的长方形.
根据同一个图形面积相等,由左图可得
(a+b)2=a2+b2+4× ab,
由右图可得(a+b)2=c2+4× ab.
所以a2+b2=c2.1.在直角三角形中,满足条件的三边长可以是 .(写出一组即可)
【解析】答案不唯一,只要满足式子a2+b2=c2即可.
答案:3,4,5(满足题意的均可) 随堂练习 4.在Rt△ABC中,∠C=90°,a=6,c=10,则b= .5.求斜边长17 cm、一条直角边长15 cm的直角三角形的面积.【解析】设另一条直角边长是x cm.由勾股定理得:
152+ x2 =172,x2=172-152=289–225=64,
所以 x=±8(负值舍去),
所以另一直角边长为8 cm,直角三角形的面积是: (cm2).通过本课时的学习,需要我们掌握:
勾股定理:
直角三角形两直角边的平方和等于斜边的平方,即课堂小结谢谢!
