人教版数学八年级下册18.2.1 矩形 第2课时 课件(27张ppt)
文档属性
| 名称 | 人教版数学八年级下册18.2.1 矩形 第2课时 课件(27张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 00:00:00 | ||
图片预览





文档简介
课件27张PPT。18.2 特殊的平行四边形
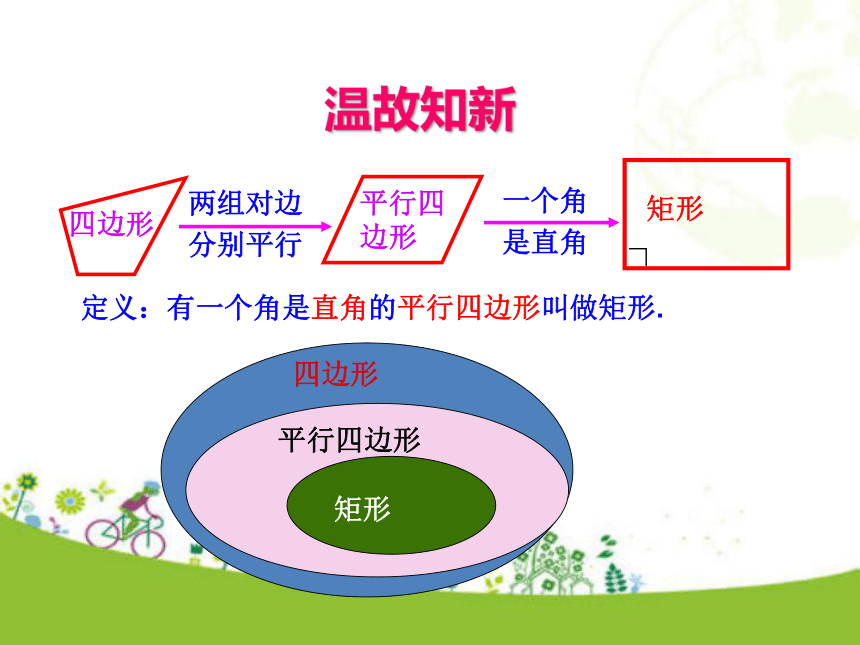
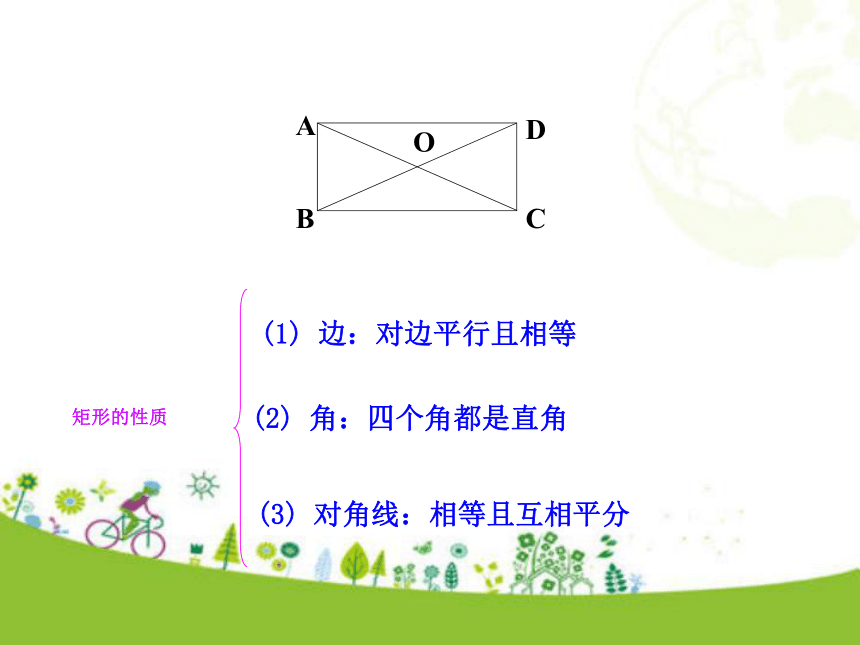
18.2.1 矩形第2课时人教版数学八年级下册2、会初步运用矩形的性质、判定等知识,解决简单的证明和计算,进一步培养学生的分析能力 .1、掌握矩形的判定方法,理解矩形的性质与判定的区别与联系.学习目标定义:有一个角是直角的平行四边形叫做矩形.温故知新矩形的性质(1) 边:对边平行且相等(2) 角:四个角都是直角(3) 对角线:相等且互相平分O有一个角是直角的平行四边形是矩形.你还有其他的判定方法吗?□ABCD∠A=90°四边形ABCD是矩形矩形判定1:(定义法)知识讲解由矩形的性质“矩形的对角线相等”我们可以猜想:
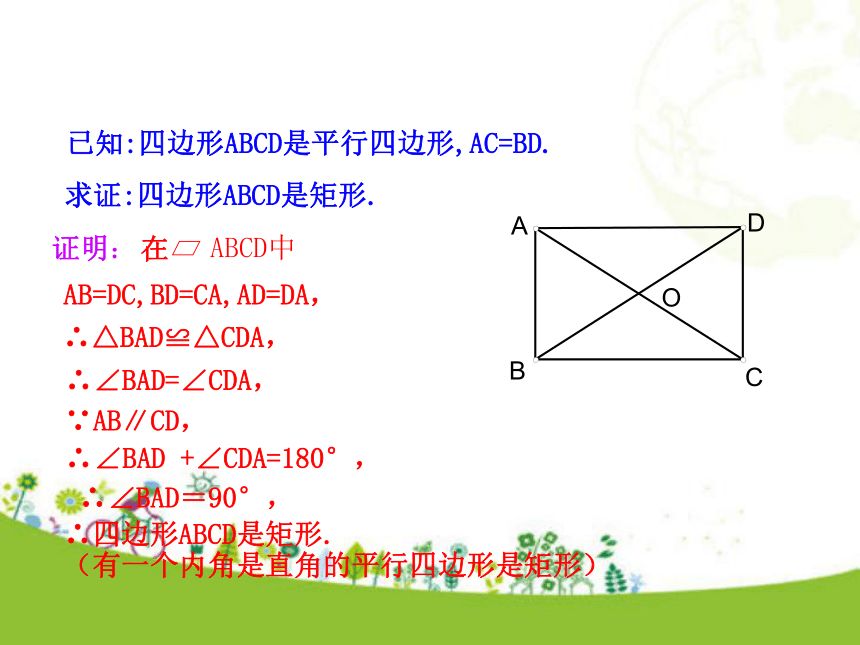
“如果一个平行四边形的两条对角线相等,那么这个平行四边形是一个矩形”.得到的图形是什么图形呢?
和你的同桌交流一下,看看是否成了一个矩形.作一个两条对角线相等的平行四边形,证明: AB=DC,BD=CA,AD=DA,∴△BAD≌△CDA,∴∠BAD=∠CDA,∵AB∥CD,∴∠BAD +∠CDA=180°, ∴∠BAD=90°, ∴四边形ABCD是矩形.
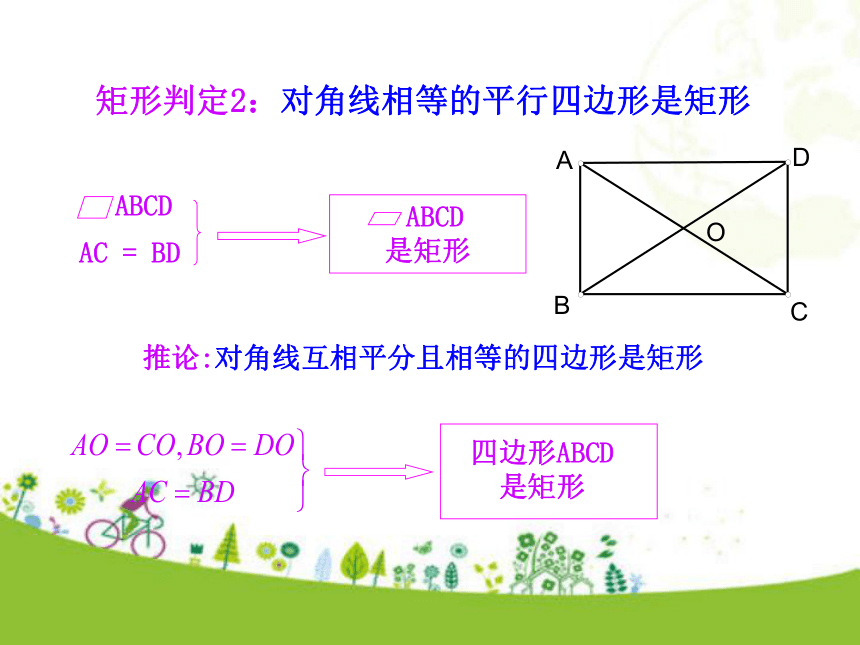
(有一个内角是直角的平行四边形是矩形)已知:四边形ABCD是平行四边形,AC=BD.求证:四边形ABCD是矩形.矩形判定2:对角线相等的平行四边形是矩形AC = BD推论:对角线互相平分且相等的四边形是矩形四边形ABCD
是矩形例 如图,O是矩形ABCD的对角线AC与BD的交点,E,F,G,H分别是AO,BO,CO,DO上的一点,且AE=BF=CG=DH.求证:四边形EFGH是矩形.证明: ∵四边形ABCD是平行四边形,
∴AC=BD (矩形的对角线相等),
AO=BO=CO=DO (矩形的对角线互相平分).
∵AE=BF =CG=DH,
∴OE=OF=OG=OH,
∴四边形EFGH是平行四边形 (对角线互相平分的四边形是平行四边形)
∵EO+OG=OF+OH,
即EG=FH,
∴四边形EFGH是矩形 (对角线相等的平行四边形是矩形).如图□ABCD中, ∠1=∠2.此时四边形ABCD是矩形吗?即学即练解:四边形ABCD是矩形.
∵四边形ABCD是平行四边形,
∴ AO=CO,DO=BO(平行四边
形的对角线互相平分).
又∵∠1=∠2,
∴AO=BO,
∴AC=BD,
∴四边形ABCD是矩形(对角线相等的平行四边形是矩形)归纳:有三个角是直角的四边形是矩形.有一个角是直角的四边形是矩形吗?有两个角是直角的四边形是矩形吗?有三个角是直角的四边形是矩形吗?已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.证明:∵∠A=∠B=∠C=90°,∴∠A+∠B=180°,∠B+∠C=180°.∴AD∥BC,AB∥CD.求证:四边形ABCD是矩形.∴四边形ABCD是平行四边形.∴四边形ABCD是矩形(有一个角是直角的平行四边形是矩形)四边形ABCD
是矩形∠A=∠B=∠C=90°矩形判定3:有三个角是直角的四边形是矩形∠A= ∠B= ∠C=90°□ABCDAC=BD□ABCD∠A=90°四边形ABCD
是矩形(1)(2)(3)归纳(1)对角线相等的四边形是矩形.
(2)有一个角是直角的四边形是矩形.
(3)四个角都是直角的四边形是矩形.
(4)对角线相等且有一个角是直角的四边形是矩形.
(5)对角线相等且互相垂直的四边形是矩形.1.判断正误即学即练A. ∠ DAB= ∠ ABC= ∠ BCD=90°
B.AB CD, AB⊥AD
C.AO=BO, CO=DO
D.AO=BO=CO=DOCO2.如图,下列条件不能判定四边 形ABCD是矩形的是( )3.矩形的两条对角线所夹的钝角为120°,短边长为5cm,则其对角线长为___________.4.已知平行四边形ABCD的对角线AC,BD相交于O,分别添加
下列条件之一:①∠ABC=90°;②AC⊥BD;③AB=BC;④AC
平分∠BAD; ⑤OA=OD.能使四边形ABCD是矩形的条件是
________.(填序号)10cm①⑤1.下列四边形中不是矩形的是( )
A.有三个角是直角的四边形是矩形
B.四个角都相等的四边形
C.一组对边平行且对角相等的四边形
D.对角线相等且互相平分的四边形C随堂练习2.如图,矩形ABCD的两对角线交于点O,过点O作AC的垂线EF,分别交AD,BC于点E,F,连接CE,已知△CDE的周长为24 cm,则矩形ABCD的周长是_____cm.
【解析】易得EF垂直平分AC,
∴EA=EC.
∵△CDE的周长为24 cm,
∴DC+DA=24 cm,
∴矩形ABCD的周长为48 cm.
答案:48证明:∵AO=BO,CO=DO,
(圆的相等半径)
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形).
∵AB=CD(圆的直径相等)
∴四边形ACBD是矩形.
(对角线相等的平行四边形是矩形)3.如图,AB,CD是⊙O的两条直径,四边形ACBD是矩形吗?证明你的结论.4.如图,MN∥PQ,同旁内角的平分线AB,BC和AD,CD分别相交于点B,D.
(1)猜想线段AC和BD间的关系是______;
(2)试用理由说明你的猜想.【解析】(1)相等且互相平分.
(2)理由:∵MN∥PQ,AB,CB分别是∠MAC,∠PCA的平分线,
∴∠BAC+∠ACB=90°,
∴∠ABC=90°,
同理∠ADC=90°,
∵CB,CD分别是∠PCA,∠QCA的平分线,
∴∠BCA+∠DCA=90°,
∴∠BCD=90°,
∴四边形ABCD是矩形.
∴AC=BD且互相平分.对角线相等的平行四边形是矩形.有一个角是直角的平行四边形是矩形.有三个角是直角的四边形是矩形.矩形的判定定理课堂小结谢谢!
18.2.1 矩形第2课时人教版数学八年级下册2、会初步运用矩形的性质、判定等知识,解决简单的证明和计算,进一步培养学生的分析能力 .1、掌握矩形的判定方法,理解矩形的性质与判定的区别与联系.学习目标定义:有一个角是直角的平行四边形叫做矩形.温故知新矩形的性质(1) 边:对边平行且相等(2) 角:四个角都是直角(3) 对角线:相等且互相平分O有一个角是直角的平行四边形是矩形.你还有其他的判定方法吗?□ABCD∠A=90°四边形ABCD是矩形矩形判定1:(定义法)知识讲解由矩形的性质“矩形的对角线相等”我们可以猜想:
“如果一个平行四边形的两条对角线相等,那么这个平行四边形是一个矩形”.得到的图形是什么图形呢?
和你的同桌交流一下,看看是否成了一个矩形.作一个两条对角线相等的平行四边形,证明: AB=DC,BD=CA,AD=DA,∴△BAD≌△CDA,∴∠BAD=∠CDA,∵AB∥CD,∴∠BAD +∠CDA=180°, ∴∠BAD=90°, ∴四边形ABCD是矩形.
(有一个内角是直角的平行四边形是矩形)已知:四边形ABCD是平行四边形,AC=BD.求证:四边形ABCD是矩形.矩形判定2:对角线相等的平行四边形是矩形AC = BD推论:对角线互相平分且相等的四边形是矩形四边形ABCD
是矩形例 如图,O是矩形ABCD的对角线AC与BD的交点,E,F,G,H分别是AO,BO,CO,DO上的一点,且AE=BF=CG=DH.求证:四边形EFGH是矩形.证明: ∵四边形ABCD是平行四边形,
∴AC=BD (矩形的对角线相等),
AO=BO=CO=DO (矩形的对角线互相平分).
∵AE=BF =CG=DH,
∴OE=OF=OG=OH,
∴四边形EFGH是平行四边形 (对角线互相平分的四边形是平行四边形)
∵EO+OG=OF+OH,
即EG=FH,
∴四边形EFGH是矩形 (对角线相等的平行四边形是矩形).如图□ABCD中, ∠1=∠2.此时四边形ABCD是矩形吗?即学即练解:四边形ABCD是矩形.
∵四边形ABCD是平行四边形,
∴ AO=CO,DO=BO(平行四边
形的对角线互相平分).
又∵∠1=∠2,
∴AO=BO,
∴AC=BD,
∴四边形ABCD是矩形(对角线相等的平行四边形是矩形)归纳:有三个角是直角的四边形是矩形.有一个角是直角的四边形是矩形吗?有两个角是直角的四边形是矩形吗?有三个角是直角的四边形是矩形吗?已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.证明:∵∠A=∠B=∠C=90°,∴∠A+∠B=180°,∠B+∠C=180°.∴AD∥BC,AB∥CD.求证:四边形ABCD是矩形.∴四边形ABCD是平行四边形.∴四边形ABCD是矩形(有一个角是直角的平行四边形是矩形)四边形ABCD
是矩形∠A=∠B=∠C=90°矩形判定3:有三个角是直角的四边形是矩形∠A= ∠B= ∠C=90°□ABCDAC=BD□ABCD∠A=90°四边形ABCD
是矩形(1)(2)(3)归纳(1)对角线相等的四边形是矩形.
(2)有一个角是直角的四边形是矩形.
(3)四个角都是直角的四边形是矩形.
(4)对角线相等且有一个角是直角的四边形是矩形.
(5)对角线相等且互相垂直的四边形是矩形.1.判断正误即学即练A. ∠ DAB= ∠ ABC= ∠ BCD=90°
B.AB CD, AB⊥AD
C.AO=BO, CO=DO
D.AO=BO=CO=DOCO2.如图,下列条件不能判定四边 形ABCD是矩形的是( )3.矩形的两条对角线所夹的钝角为120°,短边长为5cm,则其对角线长为___________.4.已知平行四边形ABCD的对角线AC,BD相交于O,分别添加
下列条件之一:①∠ABC=90°;②AC⊥BD;③AB=BC;④AC
平分∠BAD; ⑤OA=OD.能使四边形ABCD是矩形的条件是
________.(填序号)10cm①⑤1.下列四边形中不是矩形的是( )
A.有三个角是直角的四边形是矩形
B.四个角都相等的四边形
C.一组对边平行且对角相等的四边形
D.对角线相等且互相平分的四边形C随堂练习2.如图,矩形ABCD的两对角线交于点O,过点O作AC的垂线EF,分别交AD,BC于点E,F,连接CE,已知△CDE的周长为24 cm,则矩形ABCD的周长是_____cm.
【解析】易得EF垂直平分AC,
∴EA=EC.
∵△CDE的周长为24 cm,
∴DC+DA=24 cm,
∴矩形ABCD的周长为48 cm.
答案:48证明:∵AO=BO,CO=DO,
(圆的相等半径)
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形).
∵AB=CD(圆的直径相等)
∴四边形ACBD是矩形.
(对角线相等的平行四边形是矩形)3.如图,AB,CD是⊙O的两条直径,四边形ACBD是矩形吗?证明你的结论.4.如图,MN∥PQ,同旁内角的平分线AB,BC和AD,CD分别相交于点B,D.
(1)猜想线段AC和BD间的关系是______;
(2)试用理由说明你的猜想.【解析】(1)相等且互相平分.
(2)理由:∵MN∥PQ,AB,CB分别是∠MAC,∠PCA的平分线,
∴∠BAC+∠ACB=90°,
∴∠ABC=90°,
同理∠ADC=90°,
∵CB,CD分别是∠PCA,∠QCA的平分线,
∴∠BCA+∠DCA=90°,
∴∠BCD=90°,
∴四边形ABCD是矩形.
∴AC=BD且互相平分.对角线相等的平行四边形是矩形.有一个角是直角的平行四边形是矩形.有三个角是直角的四边形是矩形.矩形的判定定理课堂小结谢谢!
