人教版数学八年级下册18.2.2 菱形 第1课时 课件(26张ppt)
文档属性
| 名称 | 人教版数学八年级下册18.2.2 菱形 第1课时 课件(26张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 00:00:00 | ||
图片预览








文档简介
课件26张PPT。18.2 特殊的平行四边形
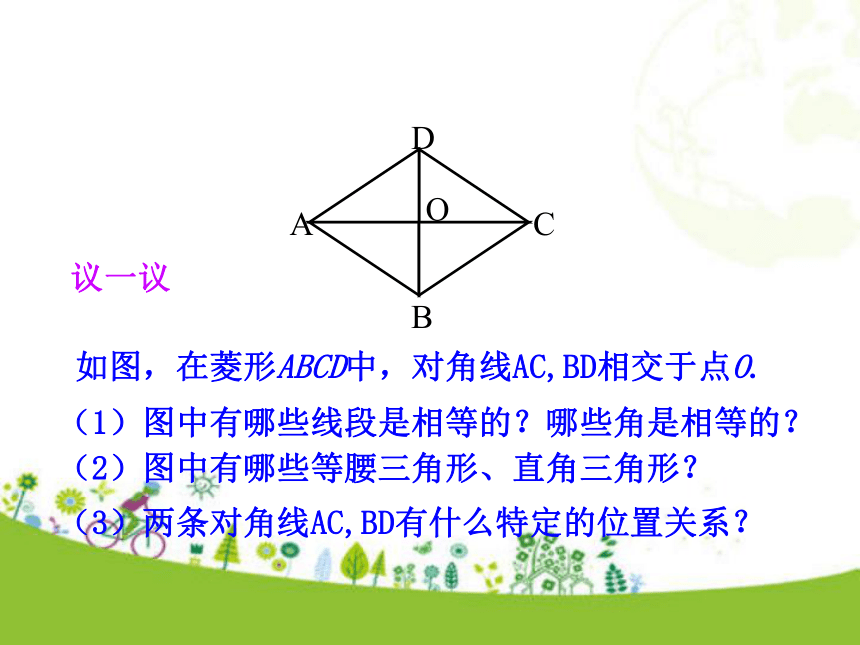
18.2.2 菱形第1课时人教版数学八年级下册2.能综合运用菱形的知识解决有关问题. 1.菱形的定义和性质.学习目标 将一张矩形的纸对折,然后沿着图中的虚线剪下,猜猜看,打开是个什么图形,自己动手做一做.新课导入上面的图案我们在生活中经常遇到,图中有很多四边形,它们是平行四边形吗?是矩形吗?它们有什么特点? 我们已经学习了特殊的平行四边形——矩形,它是从哪个角度特殊化来进行研究的?角的特殊化知识讲解菱形知识点1 平行四边形的角特殊化得到特殊的平行四边形——矩形;平行四边形的边特殊化,我们得到的特殊的平行四边形是什么,它有什么特征?菱形:有一组邻边相等的平行四边形叫做菱形.菱形也是常见的图形. 如图,在菱形ABCD中,对角线AC,BD相交于点O.
(1)图中有哪些线段是相等的?哪些角是相等的?(2)图中有哪些等腰三角形、直角三角形?(3)两条对角线AC,BD有什么特定的位置关系?议一议解:(1)AB=BC=CD=AD,
AO=CO,BO=DO,
∠DAB=∠DCB, ∠DAC=∠DCA=∠BAC=∠BCA,
∠ADC=∠ABC, ∠ADB= ∠CDB= ∠ABD= ∠CBD,
∠AOD=∠COD=∠AOB=∠COB=90°(2)等腰三角形有△ADC, △ABC ,△ABD, △BDC,
直角三角形有△ADO, △CDO, △AOB,△BCO(3)AC⊥BD∵四边形ABCD是菱形,
∴AD∥BC,AB∥CD,
AB=BC=CD=DA,
OA=OC,OB=OD,
AC⊥BD,
∠DAC=∠BAC=∠DCA=∠BCA= ∠DAB= ∠DCB,
∠ADB=∠CDB=∠ABD=∠CBD= ∠ADC= ∠ABC. 菱形具有平行四边形的所有性质. 菱形的四条边都相等,两条对角线互相垂直平分,每一条对角线平分一组对角. 验证: (1)菱形是轴对称图形吗?如果是,那么它有几条对称轴?对称轴之间有什么位置关系? (2)如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?想一想 小明是这样做的:将一张长方形的纸对折、再对
折,然后沿图(3)中的虚线剪下,打开即可得到一个菱形
的纸片.
你知道其中的道理吗?做一做(1)(2)(3)对边相等四个角都是直角 对角线互相
平分且相等四边相等对角相等两条对角线互相垂直平分,并且每一条对角线平分一组对角 若菱形的边长等于一条对角线的长,则它的一组邻角的度数分别为____________.60°和120°即学即练 比较菱形的对角线和平行四边形的对角线,我们发现,菱形的对角线把菱形分成4个全等的直角三角形,而平行四边形通常只被分成两对全等三角形.菱形性质的应用知识点2 例 如图,菱形花坛ABCD的边长为20 m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD.求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位). 1.四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=5,AO=4. 求AC和BD的长.解:∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO,BO=DO,
∴△ABO是直角三角形,
∴BO= =3
∴AC=2AO=8,BD=2BO=6即学即练 2.菱形ABCD的两条对角线BD、AC长分别是6cm和8cm,求菱形的周长和面积.解:菱形的边长= =5.
C菱形ABCD= 4×5=20(cm) 1.已知四边形ABCD是菱形,O是两条对角线的交点,AC=8cm,DB=6cm,菱形的边长是____cm. 5 2.菱形ABCD的周长为40cm,两条对角线AC∶BD=4:3,那么对角线AC=____cm,BD=____cm.1612随堂练习 3.菱形的两条对角线的长的比为3∶4,面积为24cm2,求菱形的周长. 解:设一条对角线长为3x,则另一条对角线长为4x,
S= ×3x·4x=24,∴x=2.
边长= =5.
∴菱形的周长=4×5=20(cm).4.四边形ABCD是菱形,O是两条对角线的交点,
已知AB=5cm,AO=4cm,求对角线BD的长.解析:∵四边形ABCD是菱形,∴AC⊥BD,AC平分,D∴AO2+BO2=AB2,∴BO=3,BD=6. 5.已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF. 求证:∠AEF=∠AFE. 证明:如图,连接AC,
∵四边形ABCD为菱形,
∴BC=CD,∠ECA=∠FCA.
又∵BE=DF,∴EC=FC.
∴△AEC≌△AFC,
∴AE=AF,∴∠AEF=∠AFE.拓展练习 3.菱形的两条对角线互相垂直平分,并且每一条对角线平分一组对角.1.菱形的四条边都相等.2.菱形的对角都相等.S菱形= 对角线乘积的一半菱形的性质:课堂小结谢谢!
18.2.2 菱形第1课时人教版数学八年级下册2.能综合运用菱形的知识解决有关问题. 1.菱形的定义和性质.学习目标 将一张矩形的纸对折,然后沿着图中的虚线剪下,猜猜看,打开是个什么图形,自己动手做一做.新课导入上面的图案我们在生活中经常遇到,图中有很多四边形,它们是平行四边形吗?是矩形吗?它们有什么特点? 我们已经学习了特殊的平行四边形——矩形,它是从哪个角度特殊化来进行研究的?角的特殊化知识讲解菱形知识点1 平行四边形的角特殊化得到特殊的平行四边形——矩形;平行四边形的边特殊化,我们得到的特殊的平行四边形是什么,它有什么特征?菱形:有一组邻边相等的平行四边形叫做菱形.菱形也是常见的图形. 如图,在菱形ABCD中,对角线AC,BD相交于点O.
(1)图中有哪些线段是相等的?哪些角是相等的?(2)图中有哪些等腰三角形、直角三角形?(3)两条对角线AC,BD有什么特定的位置关系?议一议解:(1)AB=BC=CD=AD,
AO=CO,BO=DO,
∠DAB=∠DCB, ∠DAC=∠DCA=∠BAC=∠BCA,
∠ADC=∠ABC, ∠ADB= ∠CDB= ∠ABD= ∠CBD,
∠AOD=∠COD=∠AOB=∠COB=90°(2)等腰三角形有△ADC, △ABC ,△ABD, △BDC,
直角三角形有△ADO, △CDO, △AOB,△BCO(3)AC⊥BD∵四边形ABCD是菱形,
∴AD∥BC,AB∥CD,
AB=BC=CD=DA,
OA=OC,OB=OD,
AC⊥BD,
∠DAC=∠BAC=∠DCA=∠BCA= ∠DAB= ∠DCB,
∠ADB=∠CDB=∠ABD=∠CBD= ∠ADC= ∠ABC. 菱形具有平行四边形的所有性质. 菱形的四条边都相等,两条对角线互相垂直平分,每一条对角线平分一组对角. 验证: (1)菱形是轴对称图形吗?如果是,那么它有几条对称轴?对称轴之间有什么位置关系? (2)如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?想一想 小明是这样做的:将一张长方形的纸对折、再对
折,然后沿图(3)中的虚线剪下,打开即可得到一个菱形
的纸片.
你知道其中的道理吗?做一做(1)(2)(3)对边相等四个角都是直角 对角线互相
平分且相等四边相等对角相等两条对角线互相垂直平分,并且每一条对角线平分一组对角 若菱形的边长等于一条对角线的长,则它的一组邻角的度数分别为____________.60°和120°即学即练 比较菱形的对角线和平行四边形的对角线,我们发现,菱形的对角线把菱形分成4个全等的直角三角形,而平行四边形通常只被分成两对全等三角形.菱形性质的应用知识点2 例 如图,菱形花坛ABCD的边长为20 m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD.求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位). 1.四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=5,AO=4. 求AC和BD的长.解:∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO,BO=DO,
∴△ABO是直角三角形,
∴BO= =3
∴AC=2AO=8,BD=2BO=6即学即练 2.菱形ABCD的两条对角线BD、AC长分别是6cm和8cm,求菱形的周长和面积.解:菱形的边长= =5.
C菱形ABCD= 4×5=20(cm) 1.已知四边形ABCD是菱形,O是两条对角线的交点,AC=8cm,DB=6cm,菱形的边长是____cm. 5 2.菱形ABCD的周长为40cm,两条对角线AC∶BD=4:3,那么对角线AC=____cm,BD=____cm.1612随堂练习 3.菱形的两条对角线的长的比为3∶4,面积为24cm2,求菱形的周长. 解:设一条对角线长为3x,则另一条对角线长为4x,
S= ×3x·4x=24,∴x=2.
边长= =5.
∴菱形的周长=4×5=20(cm).4.四边形ABCD是菱形,O是两条对角线的交点,
已知AB=5cm,AO=4cm,求对角线BD的长.解析:∵四边形ABCD是菱形,∴AC⊥BD,AC平分,D∴AO2+BO2=AB2,∴BO=3,BD=6. 5.已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF. 求证:∠AEF=∠AFE. 证明:如图,连接AC,
∵四边形ABCD为菱形,
∴BC=CD,∠ECA=∠FCA.
又∵BE=DF,∴EC=FC.
∴△AEC≌△AFC,
∴AE=AF,∴∠AEF=∠AFE.拓展练习 3.菱形的两条对角线互相垂直平分,并且每一条对角线平分一组对角.1.菱形的四条边都相等.2.菱形的对角都相等.S菱形= 对角线乘积的一半菱形的性质:课堂小结谢谢!
