人教版数学八年级下册18.2.3 正方形 第2课时 课件(25张ppt)
文档属性
| 名称 | 人教版数学八年级下册18.2.3 正方形 第2课时 课件(25张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 07:57:06 | ||
图片预览








文档简介
课件25张PPT。18.2 特殊的平行四边形
18.2.3 正方形第2课时人教版数学八年级下册2.理解正方形与平行四边形、矩形、菱形的联系和区别.1.掌握正方形的判定,并会用它们进行有关的论证和计算.学习目标菱形的判别方法:矩形的判别方法:①有一组邻边相等的平行四边形
②四条边都相等的四边形
③对角线互相垂直的平行四边形①有一个角是直角的平行四边形
②有三个角是直角的四边形
③对角线相等的平行四边形温故知新请同学们画一个四边形,要求它既是矩形又是菱形.新课导入正方形的定义:由正方形的定义可知,
正方形既是有一组邻边相等的矩形,又是有一个角为直角的菱形. 有_____________________________的
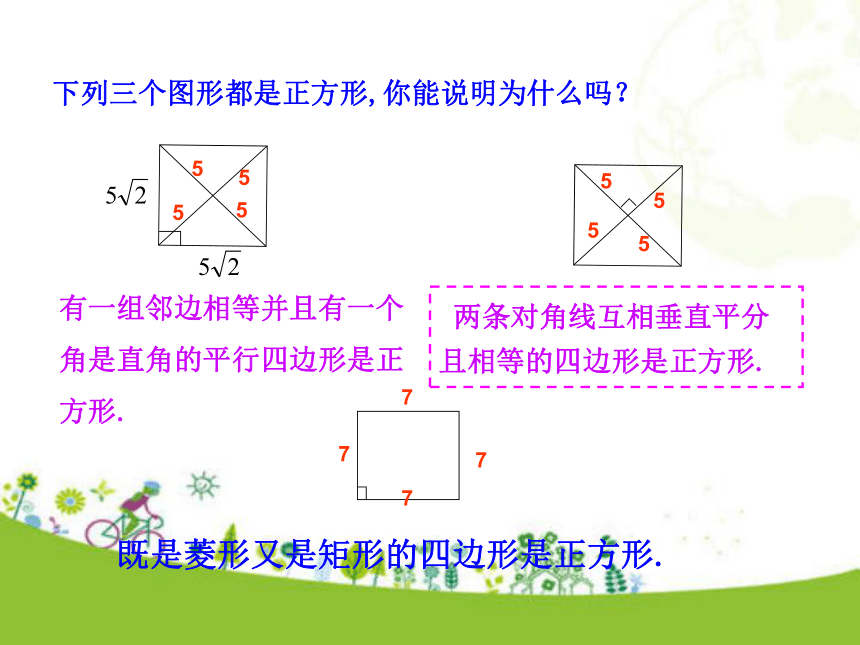
___________叫做正方形. 一组邻边相等且有一个角是直角平行四边形知识讲解有一组邻边相等有一个角是直角有一组邻边相等且有一个角是直角平行四边形有一个角是直角 有一组邻边相等通过以上回忆,你觉得什么样的四边形是正方形呢?1、要使一个菱形成为正方形需要增加的条件是( ).2、要使一个矩形成为正方形需添加的条件是( ).3、要使一个平行四边形成为正方形需要增加的条件是:( ) 有一个角是直角有一组邻边相等有一组邻边相等且有一个角是直角 如何判定一个四边形是正方形呢? 判定一个四边形为正方形的主要依据是定义,途径有两条:(1)先证它是矩形,再证它有一组邻边相等;(2)先证它是菱形,再证它有一个角为直角.下列三个图形都是正方形,你能说明为什么吗?有一组邻边相等并且有一个角是直角的平行四边形是正方形. 既是菱形又是矩形的四边形是正方形. 两条对角线互相垂直平分且相等的四边形是正方形.正方形的判定1.定义法:2.对角线法:两条对角线互相垂直平分且相等的四边形是正方形.有一组邻边相等的矩形是正方形.有一个角是直角的菱形是正方形.3.矩形菱形法:既是矩形又是菱形的四边形是正方形.1.四个角都相等的四边形是正方形.
2.四条边都相等的四边形是正方形.
3.对角线垂直的平行四边形是正方形.
4.对角线互相垂直平分且相等的四边形是正方形.
5.四条边相等且有一个角是直角的四边形是正方形.
6.对角线垂直且相等的四边形是正方形.╳╳╳√√╳即学即练例1、如图,△ABC中,∠ACB=90°,CD平分∠ACB, DE⊥BC, DF⊥AC,垂足分别为E,F. 求证: 四边形CFDE是正方形.证明:∵ CD平分∠ACB, DE⊥BC, DF⊥AC,
∴ DE=DF(角平分线上的点到角的两边距离相等).
∵ ∠DEC=∠ECF=∠CFD=90°,
∴ 四边形CFDE是矩形(有三个角是直角的四边形是矩形),
∴ 四边形CFDE是正方形(有一组邻边相等的矩形是正方形).例2、求证:对角线垂直平分且相等的四边形是正方形. 已知:如图,四边形ABCD中对角线AC,BD相交于点O,且AC=BD,AO=CO, BO=DO,AC⊥BD. 求证:四边形ABCD是正方形.证明:∵AO=CO,BO=DO, ∴四边形ABCD是平行四边形,又AC=BD, ∴平行四边形ABCD是矩形, 又∵AC⊥BD, ∴平行四边形ABCD是菱形,
即四边形ABCD是正方形.小结:正方形既是特殊的矩形,又是特殊的菱形. 要判定一个四边形是正方形,基本思路就是证明这个四边形既是菱形又是矩形,从而得到这个四边形是正方形.1.已知:如图点A′,B′,C′,D′分别是正方形ABCD四条边上的点,并且A A′=BB′=CC′=DD′,
求证:四边形A′B′C′D′是正方形.①由已知正方形证三角形全等;
②证菱形;
③再证直角;
④是正方形.证题思路分析即学即练ABCDEFG证明:过点D作DG⊥AB,垂足为G.∵AD是∠CAB的平分线,
DE⊥AC,DG⊥AB,∴DE=DG,同理:DG=DF,∴DE=DF,∵ DE⊥AC,DF⊥BC,
∴∠DEC=∠DFC=90°,又∵∠C=90°, ∴四边形CEDF是矩形,又DE=DF,∴四边形CEDF是正方形.2.在直角三角形中,∠C=90°,∠A、∠B的平分线交于点D.DE⊥AC,DF⊥BC.求证:四边形CEDF为正方形.(1)下列判断中正确的是( ) A.四边相等的四边形是正方形 B.四角相等的四边形是正方形 C.对角线垂直的平行四边形是正方形 D.对角线互相垂直平分且相等的四边形是正方形1.选择题:D随堂练习(2)在四边形ABCD中O是对角线的交点,能判定这个四边形是正方形的是( ) A.AC = BD,AB∥CD,AB=CD B.AD∥BC,∠A =∠C C.AO=BO=CO=DO,AC⊥BD D.AO=CO,BO=DO,AB=BCC(3)下列说法不正确的是( )
A.一组邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.对角线互相垂直的矩形是正方形
D.有一个角是直角的平行四边形是正方形
【解析】选D.有一个角是直角的平行四边形是矩形,不一定是正方形.2.如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,
(1)请判断四边形EFGH的形状?并说明为什么.
(2)要使四边形EFGH为正方形,那么四边形ABCD的对角线应该有怎样的情况?【解析】(1)四边形EFGH是平行四边形.
连接AC,
∵E,F分别是AB,BC的中点,
∴EF∥AC,EF= AC,
同理HG∥AC,HG= AC,
∴EF HG,
∴四边形EFGH是平行四边形.
(2)四边形ABCD的对角线垂直且相等.3.将一个菱形绕两条对角线的交点旋转90°,所得图形与原来的图形重合,此时的菱形是正方形吗?为什么?解析:是正方形,此菱形的对角线相等平行四边形矩形菱形正
方
形4.你能用恰当的方式表示出平行四边形、矩形、菱形、正方形之间的包含关系吗?谢谢!
18.2.3 正方形第2课时人教版数学八年级下册2.理解正方形与平行四边形、矩形、菱形的联系和区别.1.掌握正方形的判定,并会用它们进行有关的论证和计算.学习目标菱形的判别方法:矩形的判别方法:①有一组邻边相等的平行四边形
②四条边都相等的四边形
③对角线互相垂直的平行四边形①有一个角是直角的平行四边形
②有三个角是直角的四边形
③对角线相等的平行四边形温故知新请同学们画一个四边形,要求它既是矩形又是菱形.新课导入正方形的定义:由正方形的定义可知,
正方形既是有一组邻边相等的矩形,又是有一个角为直角的菱形. 有_____________________________的
___________叫做正方形. 一组邻边相等且有一个角是直角平行四边形知识讲解有一组邻边相等有一个角是直角有一组邻边相等且有一个角是直角平行四边形有一个角是直角 有一组邻边相等通过以上回忆,你觉得什么样的四边形是正方形呢?1、要使一个菱形成为正方形需要增加的条件是( ).2、要使一个矩形成为正方形需添加的条件是( ).3、要使一个平行四边形成为正方形需要增加的条件是:( ) 有一个角是直角有一组邻边相等有一组邻边相等且有一个角是直角 如何判定一个四边形是正方形呢? 判定一个四边形为正方形的主要依据是定义,途径有两条:(1)先证它是矩形,再证它有一组邻边相等;(2)先证它是菱形,再证它有一个角为直角.下列三个图形都是正方形,你能说明为什么吗?有一组邻边相等并且有一个角是直角的平行四边形是正方形. 既是菱形又是矩形的四边形是正方形. 两条对角线互相垂直平分且相等的四边形是正方形.正方形的判定1.定义法:2.对角线法:两条对角线互相垂直平分且相等的四边形是正方形.有一组邻边相等的矩形是正方形.有一个角是直角的菱形是正方形.3.矩形菱形法:既是矩形又是菱形的四边形是正方形.1.四个角都相等的四边形是正方形.
2.四条边都相等的四边形是正方形.
3.对角线垂直的平行四边形是正方形.
4.对角线互相垂直平分且相等的四边形是正方形.
5.四条边相等且有一个角是直角的四边形是正方形.
6.对角线垂直且相等的四边形是正方形.╳╳╳√√╳即学即练例1、如图,△ABC中,∠ACB=90°,CD平分∠ACB, DE⊥BC, DF⊥AC,垂足分别为E,F. 求证: 四边形CFDE是正方形.证明:∵ CD平分∠ACB, DE⊥BC, DF⊥AC,
∴ DE=DF(角平分线上的点到角的两边距离相等).
∵ ∠DEC=∠ECF=∠CFD=90°,
∴ 四边形CFDE是矩形(有三个角是直角的四边形是矩形),
∴ 四边形CFDE是正方形(有一组邻边相等的矩形是正方形).例2、求证:对角线垂直平分且相等的四边形是正方形. 已知:如图,四边形ABCD中对角线AC,BD相交于点O,且AC=BD,AO=CO, BO=DO,AC⊥BD. 求证:四边形ABCD是正方形.证明:∵AO=CO,BO=DO, ∴四边形ABCD是平行四边形,又AC=BD, ∴平行四边形ABCD是矩形, 又∵AC⊥BD, ∴平行四边形ABCD是菱形,
即四边形ABCD是正方形.小结:正方形既是特殊的矩形,又是特殊的菱形. 要判定一个四边形是正方形,基本思路就是证明这个四边形既是菱形又是矩形,从而得到这个四边形是正方形.1.已知:如图点A′,B′,C′,D′分别是正方形ABCD四条边上的点,并且A A′=BB′=CC′=DD′,
求证:四边形A′B′C′D′是正方形.①由已知正方形证三角形全等;
②证菱形;
③再证直角;
④是正方形.证题思路分析即学即练ABCDEFG证明:过点D作DG⊥AB,垂足为G.∵AD是∠CAB的平分线,
DE⊥AC,DG⊥AB,∴DE=DG,同理:DG=DF,∴DE=DF,∵ DE⊥AC,DF⊥BC,
∴∠DEC=∠DFC=90°,又∵∠C=90°, ∴四边形CEDF是矩形,又DE=DF,∴四边形CEDF是正方形.2.在直角三角形中,∠C=90°,∠A、∠B的平分线交于点D.DE⊥AC,DF⊥BC.求证:四边形CEDF为正方形.(1)下列判断中正确的是( ) A.四边相等的四边形是正方形 B.四角相等的四边形是正方形 C.对角线垂直的平行四边形是正方形 D.对角线互相垂直平分且相等的四边形是正方形1.选择题:D随堂练习(2)在四边形ABCD中O是对角线的交点,能判定这个四边形是正方形的是( ) A.AC = BD,AB∥CD,AB=CD B.AD∥BC,∠A =∠C C.AO=BO=CO=DO,AC⊥BD D.AO=CO,BO=DO,AB=BCC(3)下列说法不正确的是( )
A.一组邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.对角线互相垂直的矩形是正方形
D.有一个角是直角的平行四边形是正方形
【解析】选D.有一个角是直角的平行四边形是矩形,不一定是正方形.2.如图,四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,
(1)请判断四边形EFGH的形状?并说明为什么.
(2)要使四边形EFGH为正方形,那么四边形ABCD的对角线应该有怎样的情况?【解析】(1)四边形EFGH是平行四边形.
连接AC,
∵E,F分别是AB,BC的中点,
∴EF∥AC,EF= AC,
同理HG∥AC,HG= AC,
∴EF HG,
∴四边形EFGH是平行四边形.
(2)四边形ABCD的对角线垂直且相等.3.将一个菱形绕两条对角线的交点旋转90°,所得图形与原来的图形重合,此时的菱形是正方形吗?为什么?解析:是正方形,此菱形的对角线相等平行四边形矩形菱形正
方
形4.你能用恰当的方式表示出平行四边形、矩形、菱形、正方形之间的包含关系吗?谢谢!
