人教版数学八年级下册19.2.3 一次函数与方程、不等式 课件(54张ppt)
文档属性
| 名称 | 人教版数学八年级下册19.2.3 一次函数与方程、不等式 课件(54张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-19 00:00:00 | ||
图片预览










文档简介
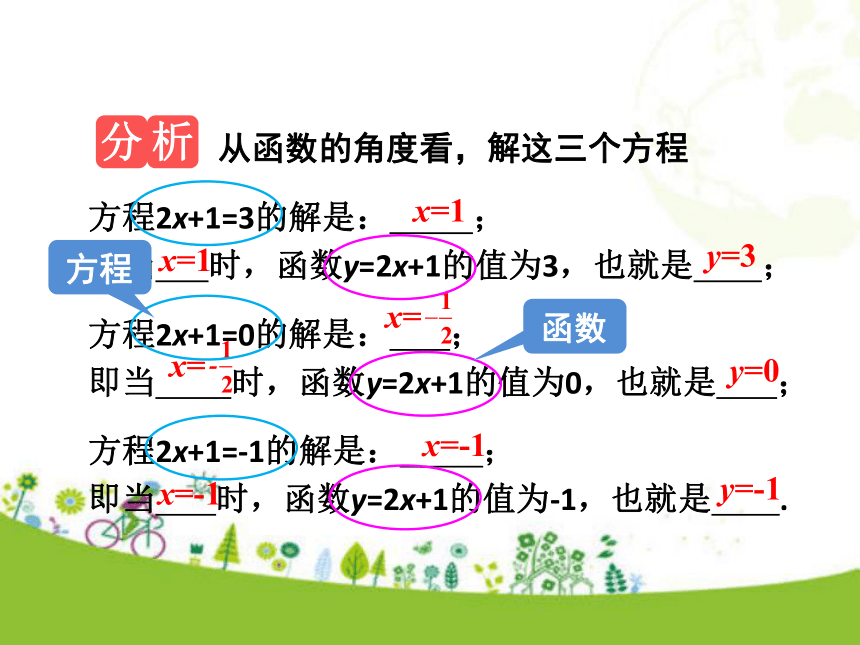
课件54张PPT。19.2.3 一次函数与方程、不等式人教版数学八年级下册数学知识之间是相互联系的,一次函数知识并不是孤立的,其实它与以前我们学过的有关知识有密切联系.今天我们来探讨一次函数与方程、不等式之间的联系.新课导入1.会从函数的角度看方程(组)解的意义.2.会从函数的角度看不等式的解集的意义.3.会将函数问题转化为解方程(组)或不等式(组)问题.学习目标知识讲解一次函数与一元一次方程知识点1相同点:等号左边都是 ,不同点:等号右边分别是 , , . 2x+130-1从函数的角度看,解这三个方程方程2x+1=3的解是: ;
即当 时,函数y=2x+1的值为3,也就是 ;方程2x+1=-1的解是: ;
即当 时,函数y=2x+1的值为-1,也就是 .方程2x+1=0的解是: ;
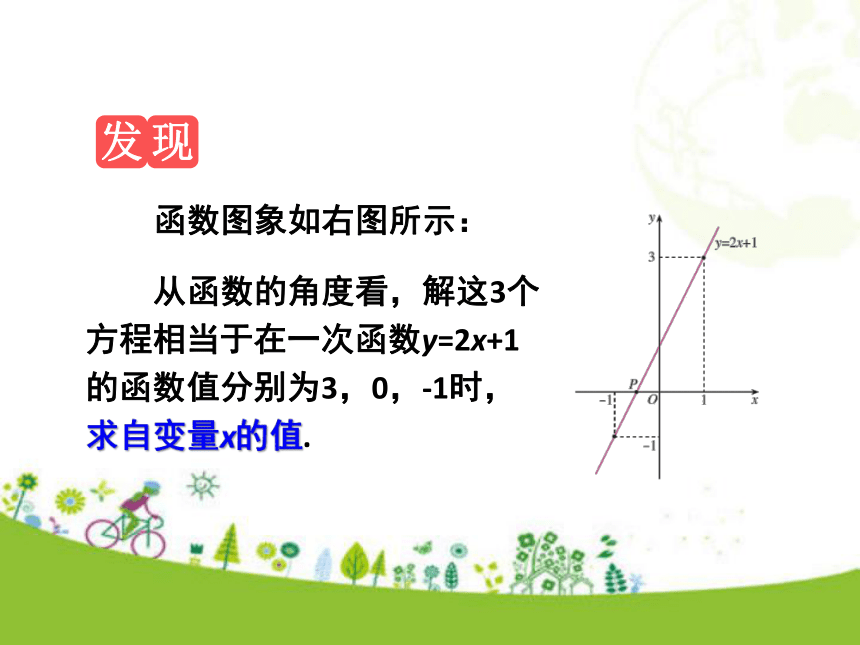
即当 时,函数y=2x+1的值为0,也就是 ;x=1x=-1x=1y=3y=0x=-1y=-1从函数的角度看,解这3个方程相当于在一次函数y=2x+1的函数值分别为3,0,-1时,求自变量x的值.函数图象如右图所示:因为任何一个以x为未知数的一元一次方程都可以变形为ax+b=0(a≠0)的形式,所以解一元一次方程相当于在某个一次函数y=ax+b(a≠0)的函数值为0时,求自变量x的值. 1.直线y=2x+b与x轴的交点坐标为(2,0),则关于x的方程2x+b=0的解是x= .2即学即练 2.若直线y=kx+6与两坐标轴所围成的面积是24,求常数k的值.解:设直线y=kx+6与x轴和y轴分别交于点A、B.令x=0,得y= 6,一次函数与一元一次不等式知识点2相同点:不等号左边都是 ,不同点:不等号右边分别是 , , . 3x+220-1从函数的角度看,解这三个方程不等式3x+2>2的解是: ;
即当 时,函数 ;不等式3x+2<-1的解是: ;
即当 时,函数 .不等式3x+2<0的解是: ;
即当 时,函数 ;x>0y=3x+2>2y=3x+2<0x<-1y=3x+2<-1x>0x<-1从函数的角度看,解这3个不等式相当于在一次函数y=3x+2的函数值分别满足大于2、小于0、小于-1的点时,求自变量x的取值范围.函数图象如右图所示:因为任何一个以x为未知数的一元一次不等式都可以变形为ax+b>0或ax+b<0(a≠0)的形式,所以解一元一次不等式相当于在某个一次函数y=ax+b(a≠0)的值大于0或小于0时,求自变量x的取值范围.在直角坐标系中,直线y=kx+3(k≠0)过点(2,2),且与x轴、y轴分别交于A、B两点,求不等式kx+3≤0的解集.解:∵直线y=kx+3(k≠0)过点(2,2),∴不等式kx+3≤0的解集为x≥6.即学即练例3 1号探测气球从海拔5米处出发,以1米/分的速度上升.与此同时,2号探测气球从海拔15米处出发,以0.5米/分的速度上升.两个气球都上升了1小时.一次函数与二元一次方程组知识点3(1)用式子分别表示两个气球所在位置的海拔(单位:米)关于上升时间(单位:分钟)的函数关系;(1)气球上升时间满足 .分析:1号气球的函数解析式为 ;2号气球的函数解析式为 .0≤x ≤60y=x+5y=0.5x+15(2)在某个时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?分析:(2)在某个时刻两个气球位于同一高度,就是说对于x的某个值(0≤x≤60),函数y=x+5和y=0.5x+15有相同的值y.则只需求出x和y的值. 容易想到解二元一次方程组:这就是说,当上升20min时,两个气球都位于海拔25m的高度.函数表达式
方程组 一般地,因为每个含有未知数x和y的二元一次方程的等式,都可以改写为( )的形式,所以每个这样的方程都对应一个一次函数,于是也对应 .这条直线上每个点的坐标(x ,y)都是这个二元一次方程的解.y=kx+b一条直线 从“数”的角度看:解二元一次方程组,相当于求自变量为何值时相应的两个函数值相等,以及这个函数值是多少;
从“形”的角度看:解二元一次方程组,相当于确定两条直线的交点坐标.因此,我们可以用画一次函数图象的方法得到方程组的解.考虑下面两种移动电话计费方式:用函数方法解答何时两种计费方式费用相等.即学即练解:设通话时间为x分,若按“方式一”计费方式,则收取费用y=30+0.3x;若按“方式二”计费方式收取费用,则收取费用y=0.4x.在同一直角坐标系中分别画出这两个函数的图象,如下图:所以两图象交于点(300,120),当x=300时,30+0.3x=0.4x,即当一个月内通话时间等于300分钟时,选择两种计费方式费用相等.【例】用作图象的方法解方程组:(1)书写步骤;
A 二元一次方程化一次函数
B 作函数图象
C 找交点
D 方程组的解
(2)书写格式.注 意y观察图象得出交点为P(2,2).如图,直线 的交点坐标是____.即学即练答案:二元一次方程组有哪些解法? 消元法二元一次方程组与一次函数有何联系?二元一次方程组的解是它们对应的两个一次函数图象的交点坐标;反之,两个一次函数图象的交点也是它们所对应的二元一次方程组的解. 正因如此,方程问题可以通过函数知识来解决,反之,函数问题也可以通过方程知识来解决.图象法是一种代数方法【规律方法】A,B 两地相距100 km,甲、乙两人骑自行车分别从A,B两地相向而行.假设他们都保持匀速行驶,则他们各自到A地的距离s(km)都是骑车时间t (h)的一次函数.1 h后乙距A地80 km; 2小时后甲距A地30 km.
问:经过多长时间两人相遇 ?直线型图表示议一议图象表示(A)04123t/hs/km
120
100
80
60
40
20
(B)【解析】可以分别作出两人
s 与t 之间的关系
图象,找出交点
的横坐标就行了! 你明白他的想法吗?
用他的方法做一做!【解析】对于乙,s 是t的一次函数,可设 s=kt+b.
当t=0时,s=100;
当t=1时,s=80.将它们分别代入s=kt+b中,可以求出k,b的值,也即可以求出乙s与t 之间的函数表达式.
同样可求出甲s与t之间的函数表达式.
再联立这两个表达式,求解方程组就行了. 你明白他的想法吗?用他的方法做一做! 用作图象的方法可以直观地获得问题的结果,但有时却难以准确,为了获得准确的结果,我们一般用代数方法.在以上的解题过程中你受到什么启发?用一元一次方程的方法可以解决问题用图象法可以解决问题用方程组的方法可以解决问题【例2】某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费y(元)是行李质量x(kg)的一次函数.现知李明带了60 kg的行李,交了行李费5元;张华带了90 kg的行李,交了行李费10元.
(1)写出y与x之间的函数表达式;
(2)旅客最多可免费携带多少kg的行李?【解析】(1)设此一次函数表达式为:y=kx+b(k≠0) . 根据题意,可得方程组 解得(2)当x=30时,y=0.所以旅客最多可免费携带30 kg的行李.某市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若某户居民应交水费y(元)与用水量x(t)的函数关系如图所示. Oy(元)x(t)15202739即学即练(2)若某用户十月份用水量为10 t,则应交水费多少元?若该用户十一月份交了51元的水费,则他该月用水多少吨?(1)分别写出当0≤x≤15和x>15时,y与x的函数关系式;【解析】(1)当0≤x≤15时,设y=kx,根据题意,可得方程27=15k,解得①当x>15时,设y=mx+n,根据题意,可得方程组 解得②(2)当x=10 时(10<15),
代入①中可得y=18;
当y=51 时(51>27),
代入②中可得x=25.B随堂练习A3.已知直线y=ax-b的图象如图所示,则关于x的方程ax-b=0的解为x= ,当x=0时,y= . 2-14.函数y=2x+6的图象如图,利用图象:(1)求方程2x+6=0的解;由图象可得:图象过点(-3,0).
∴方程2x+6=0的解为x=-3;(2)求不等式2x+6>0的解集;由图象可得:当x>-3时,函数y=2x+6的图象在x轴上方.
∴不等式2x+6>0的解集为x>-3;4.函数y=2x+6的图象如图,利用图象:(3)若-1≤y≤3,求x的取值范围.由图象可得:函数图象过F(1.5,3),G(-3.5,-1)两点,
当-3.5≤x≤-1.5时,函数y=2x+6的函数值满足-1≤y≤3,
∴x的取值范围是-3.5≤x≤-1.5.5.已知一次函数y=kx+b(k、b为常数,且k≠0)的图象(如图①).(1)方程kx+b=0的解为 ,
不等式kx+b<4的解集为 ;x=2x>0(3)在(2)的条件下,比较mx与kx+b的大小(直接写出结果).解:当x<1时,kx+b>mx;
当x=1时,kx+b=mx;
当x>1时,kx+b<mx.0<x<26.请你根据图中图象所提供的信息解答下面问题:(1)分别写出a1、a2中变量y随x变化而变化的情况;a1:y随x的增大而增大;
a2:y随x的增大而减小;拓展练习(2)求出一个二元一次方程组,使它满足图象中的两条直线的位置.求满足图象中的两条直线的位置的一个二元一次方程组,即为求直线a1、a2的解析式.∵a1过点P(1,1)和点(0,-1),
设直线a1的解析式为y=kx+b(k≠0).同理,a2的解析式为y= x+ .解得:∴a1的解析式为y=2x-1.所求二元一次方程组为一次函数与方程、不等式1.解一元一次方程:相当于在某个一次函数y=ax+b(a≠0)的函数值为0时,求自变量x的值.2.解一元一次不等式:相当于在某个一次函数y=ax+b(a≠0)的值大于0或小于0时,求自变量x的取值范围.课堂小结一次函数与方程、不等式 3.解二元一次方程组:从“数”的角度看相当于求自变量为何值时相应的两个函数值相等,以及这个函数值是多少; 从“形”的角度看相当于确定两条直线的交点坐标.谢谢!
即当 时,函数y=2x+1的值为3,也就是 ;方程2x+1=-1的解是: ;
即当 时,函数y=2x+1的值为-1,也就是 .方程2x+1=0的解是: ;
即当 时,函数y=2x+1的值为0,也就是 ;x=1x=-1x=1y=3y=0x=-1y=-1从函数的角度看,解这3个方程相当于在一次函数y=2x+1的函数值分别为3,0,-1时,求自变量x的值.函数图象如右图所示:因为任何一个以x为未知数的一元一次方程都可以变形为ax+b=0(a≠0)的形式,所以解一元一次方程相当于在某个一次函数y=ax+b(a≠0)的函数值为0时,求自变量x的值. 1.直线y=2x+b与x轴的交点坐标为(2,0),则关于x的方程2x+b=0的解是x= .2即学即练 2.若直线y=kx+6与两坐标轴所围成的面积是24,求常数k的值.解:设直线y=kx+6与x轴和y轴分别交于点A、B.令x=0,得y= 6,一次函数与一元一次不等式知识点2相同点:不等号左边都是 ,不同点:不等号右边分别是 , , . 3x+220-1从函数的角度看,解这三个方程不等式3x+2>2的解是: ;
即当 时,函数 ;不等式3x+2<-1的解是: ;
即当 时,函数 .不等式3x+2<0的解是: ;
即当 时,函数 ;x>0y=3x+2>2y=3x+2<0x<-1y=3x+2<-1x>0x<-1从函数的角度看,解这3个不等式相当于在一次函数y=3x+2的函数值分别满足大于2、小于0、小于-1的点时,求自变量x的取值范围.函数图象如右图所示:因为任何一个以x为未知数的一元一次不等式都可以变形为ax+b>0或ax+b<0(a≠0)的形式,所以解一元一次不等式相当于在某个一次函数y=ax+b(a≠0)的值大于0或小于0时,求自变量x的取值范围.在直角坐标系中,直线y=kx+3(k≠0)过点(2,2),且与x轴、y轴分别交于A、B两点,求不等式kx+3≤0的解集.解:∵直线y=kx+3(k≠0)过点(2,2),∴不等式kx+3≤0的解集为x≥6.即学即练例3 1号探测气球从海拔5米处出发,以1米/分的速度上升.与此同时,2号探测气球从海拔15米处出发,以0.5米/分的速度上升.两个气球都上升了1小时.一次函数与二元一次方程组知识点3(1)用式子分别表示两个气球所在位置的海拔(单位:米)关于上升时间(单位:分钟)的函数关系;(1)气球上升时间满足 .分析:1号气球的函数解析式为 ;2号气球的函数解析式为 .0≤x ≤60y=x+5y=0.5x+15(2)在某个时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?分析:(2)在某个时刻两个气球位于同一高度,就是说对于x的某个值(0≤x≤60),函数y=x+5和y=0.5x+15有相同的值y.则只需求出x和y的值. 容易想到解二元一次方程组:这就是说,当上升20min时,两个气球都位于海拔25m的高度.函数表达式
方程组 一般地,因为每个含有未知数x和y的二元一次方程的等式,都可以改写为( )的形式,所以每个这样的方程都对应一个一次函数,于是也对应 .这条直线上每个点的坐标(x ,y)都是这个二元一次方程的解.y=kx+b一条直线 从“数”的角度看:解二元一次方程组,相当于求自变量为何值时相应的两个函数值相等,以及这个函数值是多少;
从“形”的角度看:解二元一次方程组,相当于确定两条直线的交点坐标.因此,我们可以用画一次函数图象的方法得到方程组的解.考虑下面两种移动电话计费方式:用函数方法解答何时两种计费方式费用相等.即学即练解:设通话时间为x分,若按“方式一”计费方式,则收取费用y=30+0.3x;若按“方式二”计费方式收取费用,则收取费用y=0.4x.在同一直角坐标系中分别画出这两个函数的图象,如下图:所以两图象交于点(300,120),当x=300时,30+0.3x=0.4x,即当一个月内通话时间等于300分钟时,选择两种计费方式费用相等.【例】用作图象的方法解方程组:(1)书写步骤;
A 二元一次方程化一次函数
B 作函数图象
C 找交点
D 方程组的解
(2)书写格式.注 意y观察图象得出交点为P(2,2).如图,直线 的交点坐标是____.即学即练答案:二元一次方程组有哪些解法? 消元法二元一次方程组与一次函数有何联系?二元一次方程组的解是它们对应的两个一次函数图象的交点坐标;反之,两个一次函数图象的交点也是它们所对应的二元一次方程组的解. 正因如此,方程问题可以通过函数知识来解决,反之,函数问题也可以通过方程知识来解决.图象法是一种代数方法【规律方法】A,B 两地相距100 km,甲、乙两人骑自行车分别从A,B两地相向而行.假设他们都保持匀速行驶,则他们各自到A地的距离s(km)都是骑车时间t (h)的一次函数.1 h后乙距A地80 km; 2小时后甲距A地30 km.
问:经过多长时间两人相遇 ?直线型图表示议一议图象表示(A)04123t/hs/km
120
100
80
60
40
20
(B)【解析】可以分别作出两人
s 与t 之间的关系
图象,找出交点
的横坐标就行了! 你明白他的想法吗?
用他的方法做一做!【解析】对于乙,s 是t的一次函数,可设 s=kt+b.
当t=0时,s=100;
当t=1时,s=80.将它们分别代入s=kt+b中,可以求出k,b的值,也即可以求出乙s与t 之间的函数表达式.
同样可求出甲s与t之间的函数表达式.
再联立这两个表达式,求解方程组就行了. 你明白他的想法吗?用他的方法做一做! 用作图象的方法可以直观地获得问题的结果,但有时却难以准确,为了获得准确的结果,我们一般用代数方法.在以上的解题过程中你受到什么启发?用一元一次方程的方法可以解决问题用图象法可以解决问题用方程组的方法可以解决问题【例2】某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费y(元)是行李质量x(kg)的一次函数.现知李明带了60 kg的行李,交了行李费5元;张华带了90 kg的行李,交了行李费10元.
(1)写出y与x之间的函数表达式;
(2)旅客最多可免费携带多少kg的行李?【解析】(1)设此一次函数表达式为:y=kx+b(k≠0) . 根据题意,可得方程组 解得(2)当x=30时,y=0.所以旅客最多可免费携带30 kg的行李.某市自来水公司为鼓励居民节约用水,采取按月用水量分段收费办法,若某户居民应交水费y(元)与用水量x(t)的函数关系如图所示. Oy(元)x(t)15202739即学即练(2)若某用户十月份用水量为10 t,则应交水费多少元?若该用户十一月份交了51元的水费,则他该月用水多少吨?(1)分别写出当0≤x≤15和x>15时,y与x的函数关系式;【解析】(1)当0≤x≤15时,设y=kx,根据题意,可得方程27=15k,解得①当x>15时,设y=mx+n,根据题意,可得方程组 解得②(2)当x=10 时(10<15),
代入①中可得y=18;
当y=51 时(51>27),
代入②中可得x=25.B随堂练习A3.已知直线y=ax-b的图象如图所示,则关于x的方程ax-b=0的解为x= ,当x=0时,y= . 2-14.函数y=2x+6的图象如图,利用图象:(1)求方程2x+6=0的解;由图象可得:图象过点(-3,0).
∴方程2x+6=0的解为x=-3;(2)求不等式2x+6>0的解集;由图象可得:当x>-3时,函数y=2x+6的图象在x轴上方.
∴不等式2x+6>0的解集为x>-3;4.函数y=2x+6的图象如图,利用图象:(3)若-1≤y≤3,求x的取值范围.由图象可得:函数图象过F(1.5,3),G(-3.5,-1)两点,
当-3.5≤x≤-1.5时,函数y=2x+6的函数值满足-1≤y≤3,
∴x的取值范围是-3.5≤x≤-1.5.5.已知一次函数y=kx+b(k、b为常数,且k≠0)的图象(如图①).(1)方程kx+b=0的解为 ,
不等式kx+b<4的解集为 ;x=2x>0(3)在(2)的条件下,比较mx与kx+b的大小(直接写出结果).解:当x<1时,kx+b>mx;
当x=1时,kx+b=mx;
当x>1时,kx+b<mx.0<x<26.请你根据图中图象所提供的信息解答下面问题:(1)分别写出a1、a2中变量y随x变化而变化的情况;a1:y随x的增大而增大;
a2:y随x的增大而减小;拓展练习(2)求出一个二元一次方程组,使它满足图象中的两条直线的位置.求满足图象中的两条直线的位置的一个二元一次方程组,即为求直线a1、a2的解析式.∵a1过点P(1,1)和点(0,-1),
设直线a1的解析式为y=kx+b(k≠0).同理,a2的解析式为y= x+ .解得:∴a1的解析式为y=2x-1.所求二元一次方程组为一次函数与方程、不等式1.解一元一次方程:相当于在某个一次函数y=ax+b(a≠0)的函数值为0时,求自变量x的值.2.解一元一次不等式:相当于在某个一次函数y=ax+b(a≠0)的值大于0或小于0时,求自变量x的取值范围.课堂小结一次函数与方程、不等式 3.解二元一次方程组:从“数”的角度看相当于求自变量为何值时相应的两个函数值相等,以及这个函数值是多少; 从“形”的角度看相当于确定两条直线的交点坐标.谢谢!
